各国规范中RC框架自振周期的对比和探讨
2012-02-13阎红霞杨庆山秦敬伟
阎红霞,杨庆山,秦敬伟,李 明
(1.北京交通大学 土木建筑工程学院,北京 100044;2.河北大学 建筑工程学院,河北 保定 071002)
在RC框架结构的抗震设计中,通常采用基于弹性反应谱理论的底部剪力法或振型分解反应谱法得到结构所受的地震作用,这两种方法均需利用结构的自振周期[1]。因此,结构自振周期对RC框架结构抗震设计非常重要。目前,计算RC框架结构自振周期的方法有:经验公式、基于能量法的瑞利公式和振型分析方法。许多国家都采用这三种方法来计算结构的自振周期,且提倡采用经验公式[2-4]。众所周知,结构的自振周期是由结构质量和侧向刚度决定的。砌体填充墙的加入使框架结构侧向刚度大幅度增强,结构自振周期较大降低[4-5],各国规范在计算框架结构自振周期时均考虑到了该影响。实际工程中,为了满足建筑功能或者用户的要求,非结构构件的砌体填充墙的布置非常灵活,使结构刚度增强程度很难统一。
本文首先详细总结了国内外规范关于RC框架结构基本自振周期的取值方法,并采用这些方法对两个实际的RC框架结构(一个布置有填充墙,另一个没有布置填充墙)的基本自振周期进行了计算,将计算值和实测值进行了对比。结果表明,总体上考虑填充墙布置的得到的自振周期和实测值吻合较好,而包括我国在内的不考虑填充墙布置时经验公式的计算值,误差都很大。为了进一步探讨填充墙布置的影响,本文基于有限元软件ABAQUS,建立了考虑填充墙构件的有限元模型,其中墙体采用平面shell单元和梁柱采用beam单元模拟,并在shell单元的四角点和beam单元间耦合的方法模拟墙体和梁柱的连接,并通过对该两个实际框架结构有限元模型动力振型分析得到的结构自振周期计算值和实测值的对比,验证了模型的正确性;然后,采用该建模方式,分析了填充墙的布置对自振周期的影响,发现考虑填充墙布置的美国ASCE 7-05(2006)规范较准确,建议我国规范中RC框架结构基本自振周期计算的经验公式宜参照美国ASCE 7-05(2006)规范考虑填充墙布置。
1 国内外规范中框架结构基本自振周期的计算
国内外规范对RC框架结构基本自振周期的计算公式可以分为两大类,一类是经验公式,另一类是较精确的瑞利公式。下面具体介绍这两类公式的内容。
1.1 经验公式
框架结构基本自振周期计算的经验公式是根据实际结构的实测结果经过统计分析得到的[5],总体来说可以分为两类:忽略和考虑填充墙布置的情况。下面分类详细讨论[2-3]。
1.1.1 忽略填充墙布置的情况
以下规范中基本自振周期是框架结构总高度和底部宽度的函数:
(1)印度 IS-1893(2002)、尼泊尔 NBC-105(1995)、哥伦比亚 NSR-98(1998)、埃及(1988)、委内瑞拉(1988)和埃塞俄比亚ESCP-1(1983)国家规范中规定带填充墙的RC框架结构为式(1):

其中,Ta(s)是结构自振周期、h(m)是结构总高度,d(m)是沿着地震力作用方向结构宽度,以下同。
(2)法国AFPS-90(1990)规范建议带填充墙的RC框架结构为式(2):
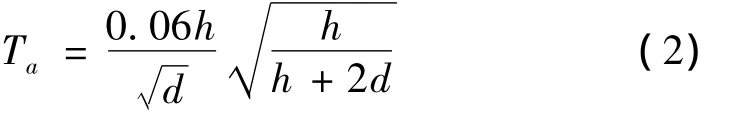
在式(1)、式(2)中,用沿地震作用方向上框架结构整个底宽d有时可能并不准确。例如,图1(c)所示填充墙的布置情况,也许取d'更合适。
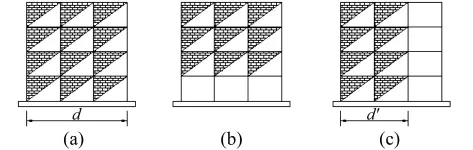
图1 填充墙在框架结构中的不同布置Fig.1 The different setting of infill in RC frame
以下规范中基本自振周期是结构楼层层数的函数:
(1)哥斯达黎加规范(1986)建议带填充墙的框架结构为式(3):

其中n是框架结构的层数,以下同。该式是考虑了填充墙增大了框架结构刚度,将纯框架结构的自振周期(Ta=0.1n)降低20%得到。
(2)意大利抗震设计规范和加拿大建筑结构规范规定采用公式Ta=0.1n计算框架的基本自振周期。
以下规范中基本自振周期是结构总高度的函数:

其中α是系数,各国取值不一样,大致在0.049~0.073范围内。以色列的抗震规范(SI-413 1995)取0.049、阿尔及利亚抗震设计规范(A05-RPA99,A05-RPA83)取0.05(并且Ta取公式(1)、公式(4)的较小值)、英国建议取 0.073。
需要指出的是阿尔及利亚抗震设计规范(A05-RPA99,A05-RPA83)规范还指出无砌体填充墙的RC纯框架结构的自振周期计算α取0.075。
我国和美国规范[6]有多个计算基本自振周期的经验公式:
(1)我国《高层建筑混凝土结构技术规程》(2002)[7]规定对于比较规则的框架结构的基本自振周期,采用近似公式计算:
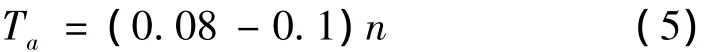
此外,《建筑结构荷载规范》(2006)[1]中指出高层建筑的RC框架结构基本自振周期的经验公式为:
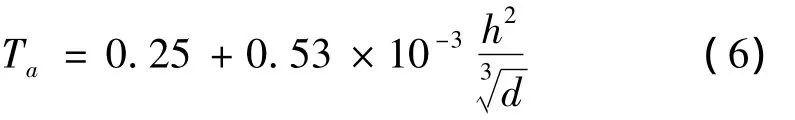
需要特别指出的是公式(5)和公式(6)都是针对高层建筑(10层及10层以上或房屋高度超过28 m的结构),而对于多层框架结构没有指明计算方法,实际工程设计中都采用这两个公式。
(2)美国 ASCE 7-05(2006)[6]规范规定,地震作用下当框架结构没有被阻止其侧移趋势的较刚性部件所包围或相连,且框架承担了全部的地震作用时(类似于纯框架结构),应采用式(7)计算框架结构的基本自振周期:

此外,该规范又指出对于不超过12层,且每层层高大于3 m且满足前面规定的条件的框架,基本自振周期的经验公式除了用公式7计算外也可以用式(8)计算。

上述估算Ta的经验公式都与填充墙布置无关,则对图1所示的三种不同的填充墙布置情况,计算出结果一样的。
目前,有少数国家规范的RC框架基本自振周期计算的经验公式考虑了填充墙的布置:
(1)Eurocode 8(2003)建议采用式(9)计算高度40 m以下的框架结构的基本自振周期:
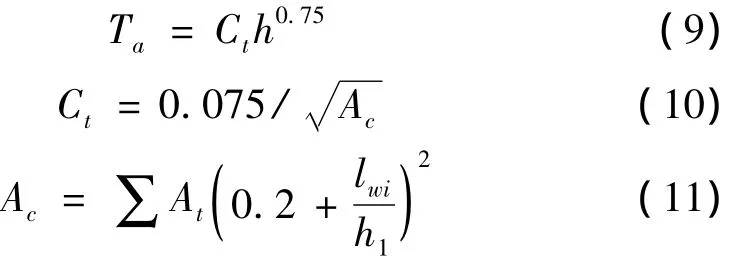
其中,Ct是针对填充墙布置的修正系数;Ac(m2)是结构首层填充墙的有效面积,At(m2)是首层填充墙i的有效截面面积,lwi(m)是首层考虑抗震方向首层填充墙i的长度,h1(m)是结构首层墙高,以下同。
(2)哥伦比亚旧规范(NSR-84 1984),采用公式1估算框架结构基本自振周期,但d的计算采用式(12)来考虑填充墙的布置。
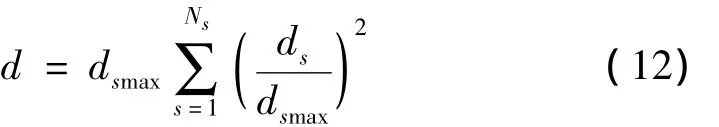
其中,Ns是考虑地震作用方向的填充墙被分割的数量;ds(m)是第s个填充墙长度、dsmax(m)最长填充墙的长度,该方法对首层无填充墙的情况(图1(b))不适用。
哥伦比亚新规范(NSR-98 1998)采用式(9),但Ct采用式(13)和式(9)计算,且不能超过0.07:
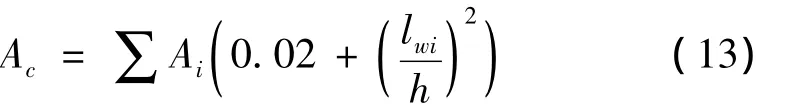
(3)菲律宾规范(NSCP 1992)指定式(9)计算基本自振周期Ta,而Ct和Ac分别采用式(14)、式(15)。
现代有轨电车的配线设置不仅需要考虑列车正常运行以及故障运行的运营功能需求,还应考虑社会车辆和交叉口的影响,同时满足有轨电车网络化运营模式的需求。
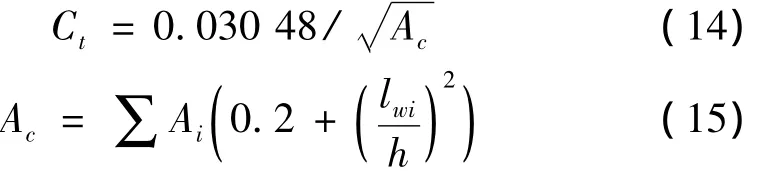
当框架结构为矩形时,为了防止填充墙的长高比lwi/h大于1,在公式(11)、公式(13)和公式(15)中都规定其值应小于等于0.9。
Eurocode 8(2003)、NSR-98(1998)和 NSCP(1992)规范都采用公式(9)计算基本自振周期,都用系数Ct考虑填充墙的布置,但仅仅考虑了首层填充墙的布置影响。对图1(b)中所示的底层没有填充墙的框架结构Ac=0,则Ct不正确。因此,可以认为在Eurocode 8和NSCP(1992)规范中是不允许框架结构首层没有填充墙。但是,这两个规范中并没有提到这一点。
(4)美国 ASCE 7-05(2006)[6]规范指出,对于填充墙和框架结构连接较好,并且限制地震作用下框架的侧向位移,框架结构基本自振周期的计算采用式(16):


其中,AB(m2)是结构底部的面积、Ai(m2)、Di(m)和hi(m)分别是第i个填充墙的面积、长度和高度,i是抵抗侧向荷载方向填充墙的数量。
1.2 瑞利公式计算框架结构自振周期
针对经验公式的局限性,如仅适合于规则框架结构,欧洲 Eurocode 8(2003)、哥伦比亚 NSR-98(1998)、哥斯达黎加Costa Rican code(1986)、委内瑞拉Venezuelan code(1988)、日本 NSCP code(1992)、阿尔及利亚Algerian code(1999)等推荐也可以使用瑞利公式(公式(18))来计算框架结构的基本自振周期Ta:

其中:wi(kg)、δei(m)、g(m/s2)和Fi(N)分别为框架第i层的结构重力,弹性变形,重力加速度和地震力。δei是根据采用经验公式得到的基本自振周期后结构分析得到的。在 Eurocode 8(2003)和 Algerian code(1999)还给出了简化的瑞利公式:

其中,Δ(m)为假想的结构顶点水平位移,即把各楼层的重力荷载代表值作为该层水平荷载加在框架结构上,计算得到的结构顶点弹性水平位移。瑞利公式是基于包括所有构件质量和刚度的结构动力计算方法。通常,规范规定瑞利公式计算得到的结构基本自振周期不应该超过按经验公式得到的20%~30%。
我国《高层建筑混凝土结构技术规程》(2002)[7]明确规定对于质量和刚度沿高度分布比较均匀的框架结构,其基本自振周期公式可按修正的瑞利计算:

其中,ψT为考虑非承重墙刚度对结构基本自振周期的折减系数,但规范中仅仅给出当非承重墙体为填充砖墙时的取值为0.6~0.7,而对于其他材料的非承重墙体并没有具体说明。式(20),通过 Δ考虑了填充墙的质量沿结构高度分布对结构周期的影响,通过ψT考虑了填充墙的刚度对结构自振周期的影响。
实际上,经验值较瑞利公式更准确,因为经验值考虑了一些结构动力计算时没有考虑的一些不确定性因素,比如非结构构件如填充墙的刚度分布问题,混凝土和填充墙材料的弹性模量等因素,这些因素将降低结构的基本自振周期。因此,许多国家将瑞利方法计算值作为上限值,防止不切实际地降低地震力设计值[3]。如英国规范规定在强震区振型分析较经验公式不得大于瑞利公式计算的1.3倍,其他地区为1.4倍;孟加拉国规范规定为1.2 倍[2]。
为了比较各国相关规范计算框架结构基本自振周期的差异和准确性,下面针对两个实际的框架结构进行基本自振周期的计算,并将其和实测值进行比较。
2 各国规范框架结构基本自振周期计算值比较
2.1 实际框架结构介绍
位于阿尔及利亚东部城市Rouiba有相邻的两个根据阿尔及利亚建筑结构抗震设计规范(1983)设计RC框架结构[9],本文将其分别称为框架1和框架2。框架1仅有现浇楼板、梁和柱;框架2是在框架1的基础上布置有粘土空心砖填充墙,它的结构尺寸和填充墙布置如图2所示。框架2平面尺寸为20.1×7.8(m2),横向两跨纵向五跨,纵向完全对称;竖向三层,每层高3.46 m,总高 10.38 m;柱截面尺寸均为 300 ×300(mm2),梁截面尺寸均为300×400(mm2),现浇楼板和填充墙的厚度分别为120 mm和240 mm。

图2 框架2结构示意图(单位mm)Fig.2 Structural diagram of frame 2(dimensions in mm)
采用Bruel和Kjaer信号采集仪,得到这两个建筑物在风激励下的振动加速度。环境风荷载可以认为是平稳白噪声激励,通过对采集的加速度信号进行快速傅里叶FFT变换,得到加速度自功率谱,然后采用峰值法,得到结构的自振周期。这两个框架结构的前三阶自振周期和振型如表1所示。由于两个框架结构的地基和基础良好,地基与上部结构的相互作用忽略不计,则砌体填充墙的加入是造成两结构周期不同的原因。从表1可知,填充墙使框架结构的基本自振周期大幅度减小,高达56.5%。

表1 框架结构的自振周期和振型Tab.1 The vibration periods and mode of frames
2.2 各国规范经验公式的计算结果
在1.1节所述的规范中,仅有美国和阿尔及利亚少数几个国家提出了对不带填充墙的框架基本自振周期的经验公式,用这些公式对框架1进行计算,结果如表2所示。从表2可知,阿尔及利亚采用公式Ta=0.075h0.75计算值和测试值之间的差距最小仅为9%,其次是美国规范的Ta=0.1n,为25%。
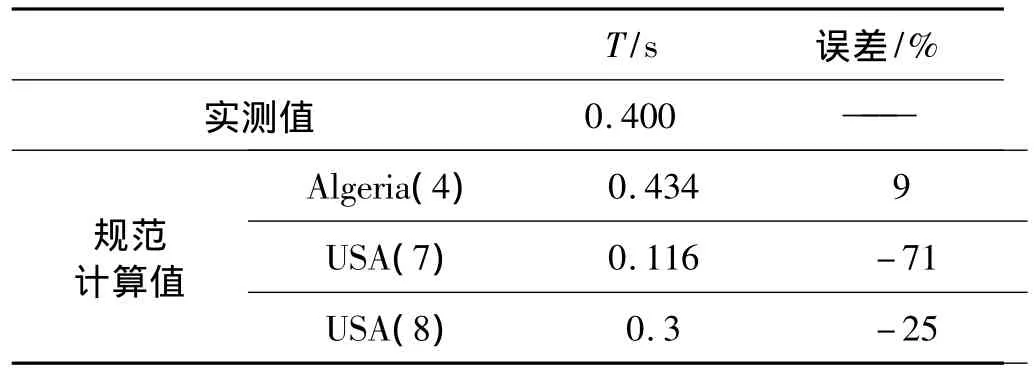
表2 结构1的基本自振周期经验公式计算值Tab.2 The fundamental periods of vibration of structure 1 using empirical formulas
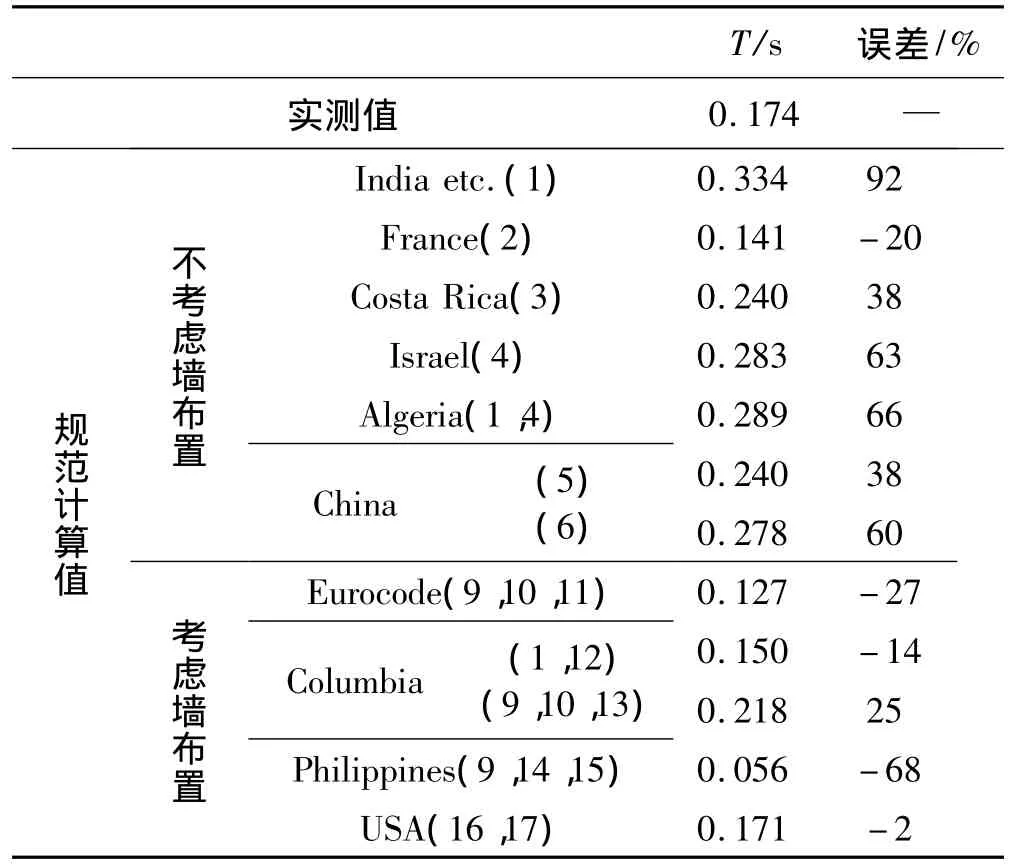
表3 结构2的基本自振周期经验公式计算值Tab.3 The fundamental periods of vibration of structure 2 using empirical formulas
采用1.1节所述各国基本自振周期计算的经验公式对框架2基本自振周期进行了计算,计算结果如表3所示。从表3可知,对于布置砌体填充墙的结构2,绝大部分不考虑填充墙布置的经验公式计算得到的基本自振周期较测试值偏大许多(公式(1)计算的竟高达92%),仅法国的较实际测试偏小,为20%。而考虑填充墙布置的经验公式的计算值却相反。总体来看,考虑填充墙布置得到的结果误差要小于不考虑填充墙布置,其中美国ASCE 7-05(2006)规范得到的误差最小,仅为2%。
2.3 各国规范瑞利公式的计算结果
根据1.2节所述的简化瑞利公式,对框架1和框架2结构基本自振周期进行了计算,结果如表4所示。从表4中可以看出,对于没有填充墙的结构1,计算结果误差较小。而对于结构2,显然两个计算结果都偏太大,计算顶点位移的时候考虑了砌体填充墙质量的影响,但折减系数0.6考虑填充墙使得该框架结构填充墙的加入使得结构刚度增大程度还远远不够。
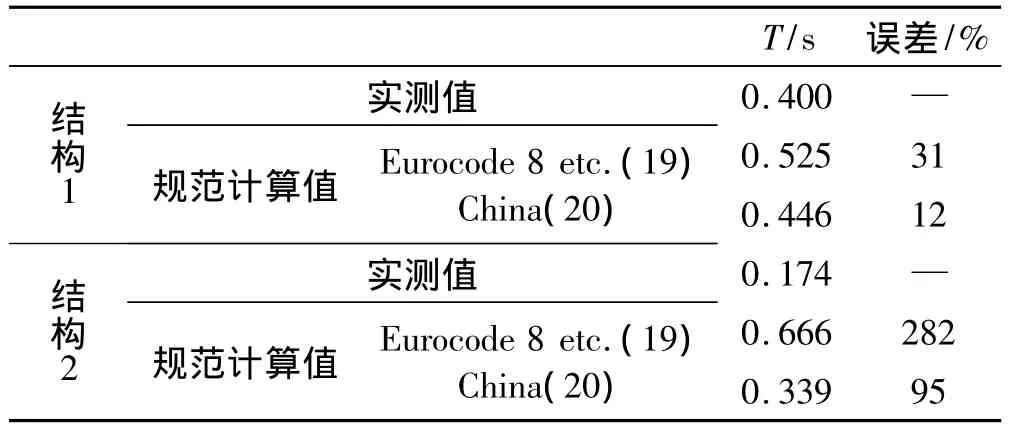
表4 结构1、2的基本自振周期瑞利方法计算值Tab.4 The fundamental periods of vibration of structure 1 and 2 using Rayleigh method
前面讨论方法,不管是经验公式还是瑞利公式得到的仅是框架结构的基本自振周期,这对底部剪力法足够了,但对振型分解反应谱法而言,就应采用其他的计算手段,如特征值分析法得到所需的多阶振型自振周期。下面,讨论如何建立较准确的框架结构有限元模型,以便于用动力分析得到多阶振型和周期。
3 计算RC框架结构自振周期有限元模型的探讨
RC框架结构的有限元模型,通常beam单元来模拟RC框架结构的梁、柱结构构件,shell单元来模拟现浇楼板,忽略了非结构构件填充墙,这种方法建立的模型针对框架静力竖向荷载的分析是趋于安全的。但是,实际中由于填充墙的加入增大了框架结构的刚度,模型中没有考虑填充墙会使模型较实际结构偏柔,最终导致模型动力分析得到的自振周期计算值较真实值偏大很多,从而不可采用。因此,传统的模型已不在适合计算结构的自振周期。在计算框架结构自振周期时填充墙的模拟,Chaker等[10]指出有限元中平面应力单元较对角斜撑模型更准确。下面,以有限元软件ABAQUS为平台,探讨计算框架结构自振周期的有限元模型。
3.1 有限元模型
基于ABAQUS平台建立框架结构的有限元软件模型:结构构件梁、柱采用beam单元,现浇楼板、填充墙采用shell单元,根据结构1和结构2的实际尺寸建立有限元模型1和2,并赋予相应的材料属性(密度、弹性模量和泊松比)。框架梁beam单元和现浇楼板shell单元之间采用constraint中的tie连接,保证框架梁和现浇楼板的刚性连接,在选择楼板作为从属面的时候选择sufarce,可以保证楼板在平面内刚度无限大;填充墙shell单元四个角点和梁柱节点处采用constraint中coupling方法模拟墙和梁柱的连接,如图3(a)所示(为了清楚,将梁柱和填充墙分开显示)。图3中的(b)和(c)分别是结构1和结构2的有限元模型。对于网格类型,Beam单元采用B31,shell单元采用S4R。模型1和模型2采用ABAQUS/Standard中特征值分析的Lanczos方法进行动力分析,得到这两个模型的自振周期和振型,下面对计算结果进行分析对比。

图3 有限元模型Fig.3 The model of FEA
3.2 动力振型分析的结果
按3.1节所述的有限元动力分析得到两个模型的振型和实测结果一致,依次为横向、纵向和扭转;对于前三阶结构自振周期,模型 1 为 0.394 s、0.383 s和0.344 s,模型2 为0.178 s、0.152 s和0.137 s。将有限元计算结果和2.1节所述实测值进行比较,如图4所示。从图4可知,有限元计算和实测的结果非常接近,对基本自振周期,模型1和2误差仅仅为1.5%和2.3%。因此,本文建议的计算自振周期的有限元模型正确。

图4 自振周期对比Fig.4 The comparison of vibration periods
4 填充墙的布置对自振周期的影响分析
通过2.2节的分析,发现考虑填充墙布置的计算框架结构的基本自振周期的经验公式相对要准确,为了进一步探讨具体影响,对图1所示三种情况,采用3.1节叙述的建立具有填充墙的框架结构有限元模型的方法,对图1的三个结构进行了振型分析,具体的结构尺寸如下:
图1所示的三个框架结构,纵向和横向完全对称,横向三跨纵向四跨,每跨均为4×4(m2),整个结构平面为16×12(m2),竖向四层,每层高 3.5 m,总高14m;柱尺寸均为 300×300(mm2),梁尺寸均为300×400(mm2),楼板和填充墙的厚度分别为120 mm和240 mm,图5是有限元模型示意图(没有显示填充墙的布置)。
将图5所示的有限元模型,每层满布填充墙(如图1(a)所示)时,振型分析得到的第一阶自振周期为0.187 s,规范 NSR-84中经验公式(公式(1)和公式(19)计算得到)计算值为0.188 s;美国 ASCE 7-05(2006)规范(式(20)和式(21)计算得到)计算值为0.109 s。这两个经验公式和结构动力分析的结果较接近。
将图5所示的有限元模型,依次设置首层(图1(b))到第四层没有布置填充墙时,得到的结构基本自振周期为0.419 s、0.388 s、0.316 s和0.214 s。相对于填充墙满布时的基本自振周期0.187 s,周期增大倍数依次为2.24、2.07、1.69 和1.14 倍。对于建筑功能的要求,填充墙在首层缺少的情况比较多,而这种情况对结构的自振周期影响最大。考虑填充墙布置的规范中仅NSR-98中的经验公式可以计算首层没有布置填充墙的情况,对该结构的计算值为0.506 s,该值和有限元计算值0.419 s的误差比较小,为17%。可见,基本自振周期计算的经验公式仅考虑首层填充的布置是合理的。
图5 三维有限元模型Fig.5 3-D finite element model
将图5所示的有限模型,按图1(c)中所示进行填充墙布置,分析的得到结构的第一阶自振周期为0.219 s。和满布时的到的周期0.187 s相比差19%,差别不是特别大。此时,式(2)若取d为填充墙布置的宽度8 m得到的为0.203 s和动力分析结果很接近,如按d为12 m得到的为0.147 s,差别较大,可见d的取值应该考虑填充墙的布置情况。在经验公式中,应该通过参数的设定,考虑首层填充墙的填充率。
5 结论
通过本文分析,可以得出以下结论:
(1)框架结构基本自振周期计算的经验公式宜考虑填充墙布置的影响,并宜参照美国 ASCE 7-05(2006)规范,根据填充墙和框架连接情况分别考虑。
(2)对于填充墙和框架连接较好,填充墙限制结构侧向位移时,建议参照美国ASCE 7-05(2006)和NSR-84规范:经验公式宜取框架结构总高度的函数,系数考虑首层填充墙的布置,但取值还需根据我国实际情况,通过大量的实际结构测试值和结构动力分析来确定。
(3)我国规范中瑞利公式考虑了填充墙的布置和刚度对自振周期的影响是比较合理的,折减系数的选取应该进一步细化。
(4)对带填充墙的框架结构建立本文提出的有限元模型,并采用特征值分析的办法能获得较准确的多阶自振周期。
[1]GB 50011-2010.建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.
[2]Kaushik H B,Rai D C,Eeri M,et al.Code approaches to seismic design of masonry-infilled reinforced concrete frames:a state-of-the-art review[J].Earthquake Spectra,2006,22(4):961-983.
[3]Amanat K M,Hoque E.A rationale for determining the natural period of RC building frames having infill[J].Engineering Structures,2006,28:495-502.
[4]王广军.钢筋混凝土房屋自振周期的经验公式[J].四川建筑科学研究,1990,1:31-36.
[5]张 慧.填充墙对框架结构体系自振周期的影响[J].水电能源科学,2008,26(6):102-104.
[6]ASCE/SEI 7-05.Minimum design loads for buildings and other structures[S].Virginia:American Society of Civil Engineers,2006.
[7]JGJ 3-2002.高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2002.
[8]GB 50009-2001(2006版).建筑结构荷载规范[S].北京:中国建筑工业出版社,2006.
[9]Chaker A A,Cherifati A.Influence of masonry infill panels on the vibration and stiffness characteristics of RC frame buildings[J]. Earthquake Engineering and Structural Dynamics,1999,28:1061-1065.
[10]Chaker A A,Cherifati A.Influence of masonry infill panels on the vibration and stiffness characteristics of R/C frame buildings[J]. Earthquake Engineering and Structural Dynamics,1999,28(9):1061-1065.
