基于力耦合的非谐振单元组成的超声变幅器设计

王时英，吕 明，轧 刚

（太原理工大学 机械工程学院，太原 030024）

超声在工业、农业、医疗、军事等诸多领域发挥了巨大的作用，超声应用的关键技术是如何产生相应的超声能量，为了使超声电能最大效率地转换为机械振动能量，超声振动系统按“全调谐”方式工作［1］。此时超声电源和变幅器有相同的谐振频率，变幅器的结构尺寸是由超声振动系统的谐振频率决定的。根据全谐振设计理论，变幅器可以按半波长及其整数倍分为变幅杆、圆盘等若干个振动单元，按照谐振频率分别设计每个振动单元的结构尺寸，并串联组装起来，振动系统会在这一频率上谐振。基于此，许多学者对单个变幅杆及圆盘振动特性进行了研究［2-5］。在超声珩磨工艺中，变幅器作为加工工具的组成部分，其中的变幅杆和圆盘结构尺寸可以由系统谐振频率确定，可以用全谐振理论设计，而超声珩齿工艺中，变幅器中的齿轮（简化为圆盘）的结构尺寸是由它的使用要求决定，无法用现有的全谐振理论进行设计，针对这个情况，提出了非谐振单元变幅器设计理论［6］，将结构尺寸不能任意确定的齿轮与结构尺寸可以任意确定的变幅杆组成复杂超声振动系统，通过调整变幅杆的结构及尺寸，采用力耦合条件联合设计变幅杆和齿轮，使齿轮与变幅杆组成的复杂超声振动系统谐振于要求的频率范围，满足超声珩齿要求。

1 超声珩齿振动系统的组成及其数学模型的建立

1.1 超声珩齿振动系统的组成

珩齿是将被珩齿轮通过心轴安装在珩齿机工作台的前后顶尖上，由装在主轴上的珩轮带动齿轮高速旋转实现珩削加工。超声珩齿振动系统将替代心轴和珩齿机一端顶尖安装在珩齿机上，因此设计了如图1所示的超声珩齿夹具，它是由换能器、传振杆及变幅器（阶梯型变幅杆及齿轮组成）实现超声振动；传振杆在节点与套筒连接，套筒通过轴承固定在夹具体上，夹具体固定在珩齿机工作台上；变幅器用螺纹连接在传振杆上，被加工齿轮通过内孔连接在变幅杆上，并通过螺纹紧固。珩齿加工时，珩轮带动齿轮、变幅杆及换能器高速旋转，因此换能器的电源采用电刷接入。

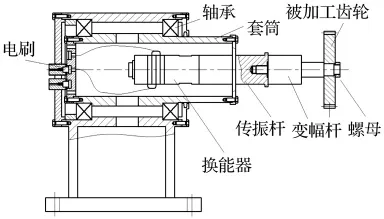
图1 超声珩齿夹具Fig.1 Jig of ultrasonic honing

1.2 超声珩齿振动系统的数学模型

超声换能器、传振杆、变幅器的结构尺寸为二分之一波长，按照全谐振设计理论，可以将变幅器从振动系统中分离出来单独进行分析。齿轮可简化为外径等于齿轮分度圆直径、内径等于齿轮孔径的环盘。由于变幅杆、齿轮及紧固螺母三者材料相同，且连接牢靠，可以将它们看作一个整体刚性连接振动结构；螺母以及超出被加工齿轮厚度的螺杆由于尺寸较小而忽略，齿轮变幅器对应的简化数学模型如图2所示。建立柱坐标系r，θ，z，坐标系原点在阶梯变幅杆大小截面突变中心位置。其中变幅杆的大端直径为D1=2R1，小端直径为D2=2R2，环盘的厚度为2h，直径为D3=2R3，大端位移为ξ1，小端位移为 ξ2，环盘的弯曲振动位移为w，变幅杆大端与小端截面突变处的圆弧半径为R4。

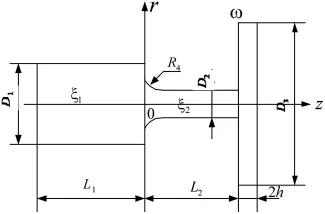
图2 阶梯型变幅器的数学模型Fig.2 Mathematical model of the step transformer

阶梯型变幅器的边界条件为：

（1）变幅杆的大端与换能器在z=-L1连接，换能器输出的位移最大，故变幅杆左端处位移最大，即位移导数为零：

其中，L1=λ/4。

（2）在z=0处，由于截面跃变，情况较复杂。如果截面比不是很大，可以认为位移和应力是连续的［7］。此处，有：

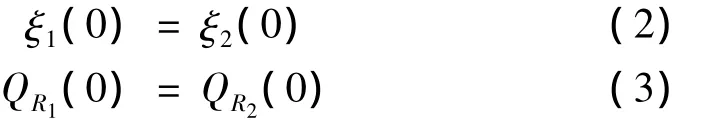
其中，QRi（i=1，2）为材料内的应力。

（3）变幅杆与环盘在z=L2处相连，变幅杆的位移应等于盘的位移：

（4）在z=L2处，变幅杆所受的轴向力与盘内孔面所受的剪力相等，即：

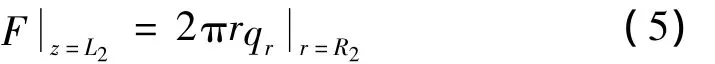
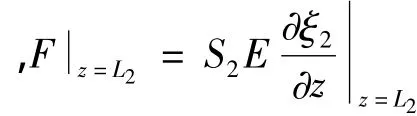
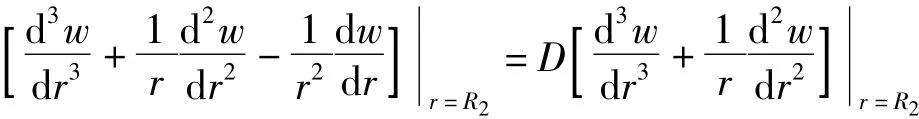
D为盘的弯曲刚度。

（5）当r=R2时，变幅杆与环盘内缘可以看做刚性连接，环盘此处的挠曲率为零：

（6）环盘作边界自由的弯曲振动，当r=R3时，所受的弯矩为零，即：

剪切力也为零，即：

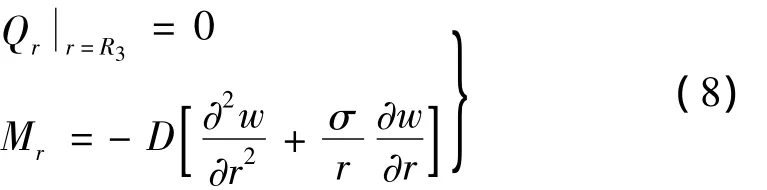
S2为阶梯形变幅杆小端横截面积。

2 阶梯型变幅器的频率方程及求解

阶梯型变幅杆的纵向振动大端的位移方程为：

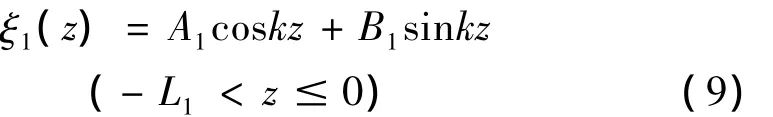
小端的位移方程：

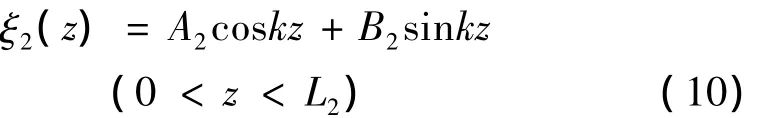
在实际加工中，要求环盘作只有圆节线的弯曲振动，环盘的振动位移分布（R2≤r≤R3）为：

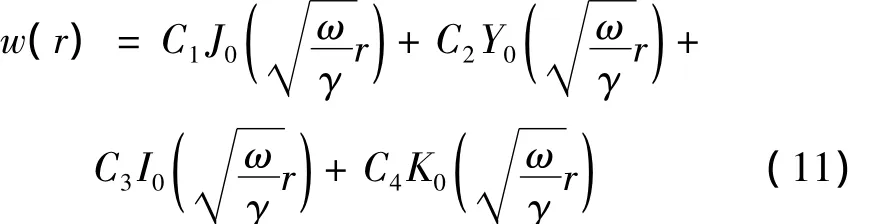
式中，C1、C2、C3、C4为积分常数

（4）边界条件和耦合条件

将式（9）～式（11）及其导数代入式（1）～式（8）得到下列方程：

将方程（12）～方程（19）变成形式：

其中常数Pij（i，j=1，2，3，4，5，6，7，8）是方程（12）～ 方程（19）的A1、B1、A2、B2、C1、C2、C3、C4对应的系数，因为它们不全部为零，那么上述8个方程的系数行列式等于零：

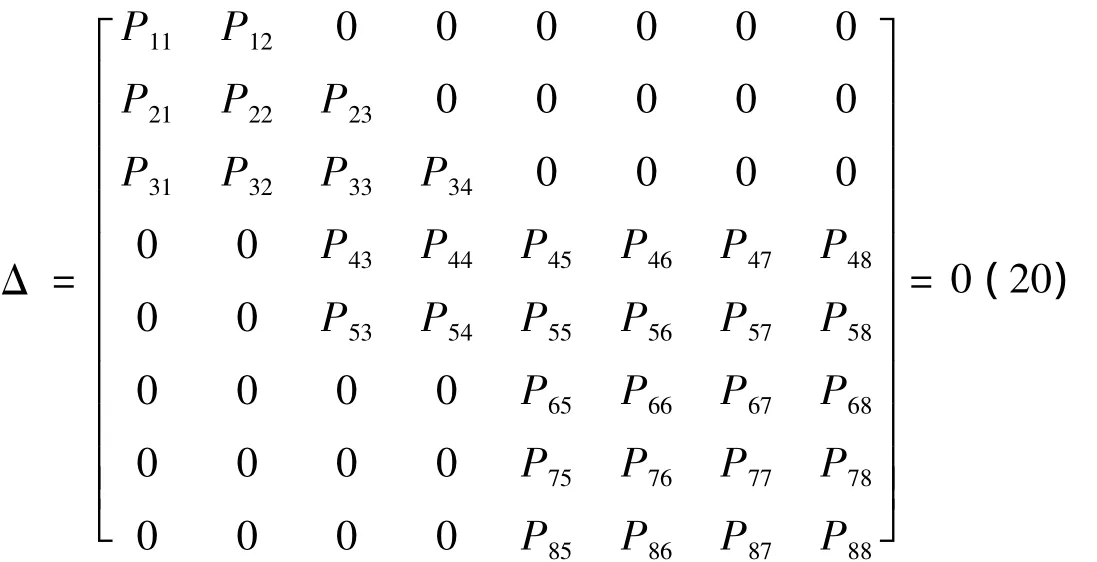
上式即为变幅器的频率方程，此方程与L2和系统的谐振频率f有关，可以通过改变这两个参数使Δ=0，此时的长度即为变幅器在此频率下的谐振的设计参数。

设振动系统的谐振频率为15 kHz，变幅器的材料选用45钢，其材料常数即设计计算材料常数为：弹性模量为2.092 ×1011N/m2，泊松比为 0.29，材料密度为7 810 kg/m3。根据换能器尺寸确定R1=37.5 mm，变幅器的其它尺寸为R2=18 mm，R3=60 mm，h=6 mm。变幅杆的大截面长度L1取定值，L1=λ/4=81 mm。取L2的变化范围从10 mm到450 mm，在MATLAB软件中编程，以L2为横坐标，以求出频率方程（20）的值Δ作为纵坐标，绘制出如图3的曲线，在最靠近Δ=0的L2值有三个，分别为 86.25 mm，258.8 mm，431.3 mm。

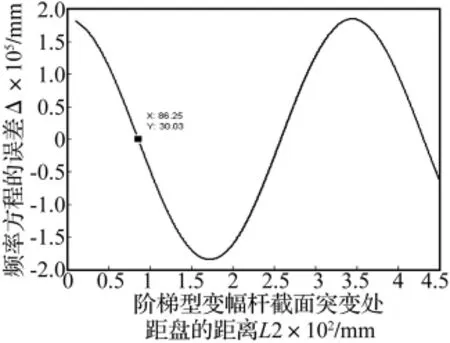
图3 频率 f=15 kHz时，L2的长度变化时频率方程解的误差Fig.3 f=15 kHz，the relationship between L2 and error of frequent equation’s solution

考虑到变幅器结构尽量紧凑，取L2=86 mm。这样，就确定了阶梯型变幅器的非谐单元—变幅杆的长度，从而确定了整个变幅器的结构尺寸。

如果按照全谐振设计（把阶梯形变幅杆作为单一变幅杆进行设计，谐振频率为15 kHz），那么，大端和小端的长度应该相等，即L1=L2=λ/4=81 mm。然而按非谐理论设计，实际求得L2＞L1，说明非谐理论应用的必要性。

3 阶梯型变幅器的模态分析

为了验证理论设计变幅器的振动模态，在ANSYS中建立如图4所示的变幅器模型，单元类型选择SOLID45，智能划分网格，网格精度等级为3，进行模态分析，提取十阶频率，频率搜索范围为10 kHz到20 kHz。

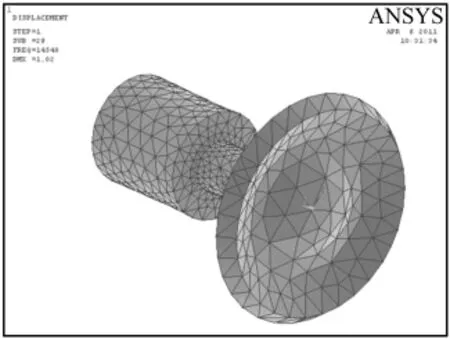
图4 阶梯型变幅器的有限元模型及振型Fig.4 Finite element mode and its vibratory mode of the step transformer

模态分析后，变幅器在14.548 kHz时的振型如图4所示。从ANSYS模态仿真振型来看，阶梯型变幅杆作纵向振动；与变幅杆相连的圆盘作纯圆节线的弯曲振动，而且整个振动系统的谐振于14.548 kHz，与设计理论相差0.452 kHz。这说明，用解析法设计的变幅器是一种有效的、比较可靠的变幅器设计理论。

4 变幅器的谐振频率测试及振动实验

采用敲击法测试变幅器的谐振频率，实验装置如图5所示。电荷放大器型号为YE5854；示波器型号为TDS1012，测试频率100 MHz；压电加速度传感器型号为CA-YD-125，质量仅1.2 g。把变幅器平放在泡沫板上，在圆盘的中央用胶粘上传感器。测试时用小锤敲击变幅器的一端，实验测得变幅器响应波形如图6所示。

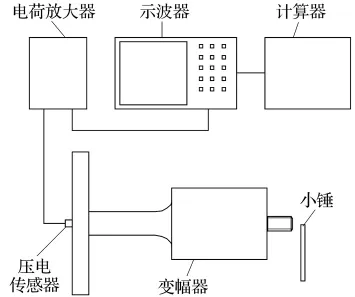
图5 实验装置示意图Fig.5 Sketch of experimental device

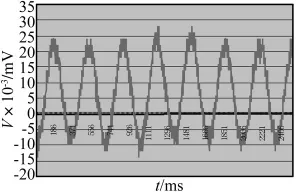
图6 敲击法得到的波形图Fig.6 Waveforms measured by the transformer’s strike

在示波器中，由于三个周期的波传播用时50 μs×4=200 μs，那么该波的频率为：

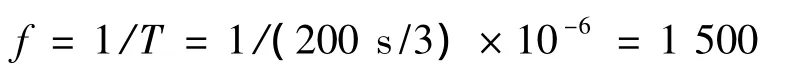
即该变幅器的固有频率为15 kHz，与设计频率吻合。

把阶梯型变幅器与超声波换能器连接，在盘上均匀撒上少量细沙，接通电源，细沙迅速在圆盘上排列成一个圆圈，如图7所示，说明圆盘的确在作纯圆节线的弯曲振动，此时系统的振动频率为15.623 kHz，进一步说明理论设计结果正确。

图7 阶梯形变幅器振型Fig.7 The vibrational shape of step transformer

5 结论

齿轮的结构尺寸是由它的使用要求决定，与由超声振动系统谐振频率决定的尺寸相差较大，因此是一种非谐振单元，本文采用力耦合方法，将齿轮简化为圆盘，将它和变幅杆组合设计，实现了谐振于某一频率的超声变幅器可以由不谐振于此频率的变幅杆和环盘组成的设计。经有限元分析及实验测试，设计变幅器的谐振频率及振动模态与理论预期结果一致，说明本文提出的非谐单元组成的变幅器的动力学设计方法是可行、有效的。

［1］曹凤国，张勤俭.超声加工技术的研究现状及其发展趋势［J］.电加工与模具，2005，（增刊）：25-31.

［2］刘世清，林书玉，王成会.锥形剖面环形聚能器径向振动等效电路研究［J］.陕西师范大学学报 ，2005，（33）：31-33.

［3］ Wang D S，Zhou A P，Liu C S，et al.Study of acoustics characteristics of bending vibration disc-theoretical analysis［J］.Key Engineering Materials，2001，202：359-363.

［4］Lee H，Singh R.Acoustic radiation from out-of-plane modes of an annular disk using thin and thick plate heories［J］.Journal of Sound and Vibration，2005，（282）：313-339.

［5］王时英，吕 明，轧 刚.圆锥过渡复合变幅杆动力学特性研究［J］.太原理工大学学报，2007，38（2）：95-97.

［6］王时英，吕 明，轧 刚.超声珩齿指数型变幅器的动力学特性［J］.机械工程学报，2007，43（6）：190-193.

［7］刘井权，闫久春，杨士勤.超声刀切割系统的模态分析［J］.哈尔滨工业大学学报，2001，33（4）：435-438.

［8］林仲茂.超声变幅杆的原理和设计［M］.北京：科学出版社，1987：190-210.

［9］ ARPACI A.Annular plate dampers attached to continuous system［J］.Journal of Sound and Vibration，1996，191（5）：781-793.