基于混沌激励与吸引子分析的结合面损伤识别方法

裘群海，徐 超，吴 斌

（西北工业大学 航天学院，西安 710072）

工程结构在使用寿命周期内，受到各种环境因素，如温度、振动、冲击等作用，连接结合面可能出现滑动、分离和松脱等损伤现象，从而严重影响结构的完整性、功能性和安全性。因此，发展有效的理论和方法来准确地识别和监测在役结构结合面的损伤状态，对于保证结构安全、避免重大安全事故和降低事故危害性具有重要的实际意义和应用价值。

基于振动分析的健康监测方法是实现自主化、智能化和在线式结构损伤识别的极具潜力的方法，正日益受到广泛的关注［1］。这类方法的基本思想是利用外部振动激励下待测结构系统的动力响应信息，借助统计分析、信号处理、系统辨识或动力学理论提取出表征结构状态的特征参量，并将其与参考状态对比，从而识别出结构当前的损伤状态。结构基本动态特性，如固有频率、模态振型、振型斜率、模态阻尼比、动柔度、频响函数、功率谱等，因具有物理概念清晰、计算简单等优点，在结构损伤识别中被大量用作特征参量。但是，这些参量大多依赖于对结构的线性化模型假设，且参量本身主要表征的是结构整体的动态特性，因此存在对小损伤状态识别灵敏度低或对非线性结构系统适用性差的问题［2］。

一般的，含损伤结构本质上都是非线性系统，特别是在某些损伤状态下，动力响应具有明显的非线性特征。基于非线性动力学理论的结构损伤识别方法近年来被提出并获得快速发展［3］。按照非线性动力学理论，系统可在相空间中描述。此类方法的基本思想是：首先利用非线性时间序列分析方法和系统动力响应信息，重构出与待测结构系统等价的吸引子，进而研究吸引子的几何特性，提取出与结构状态一一对应的特征参量，从而实现对损伤状态的识别。系统吸引子中包含有丰富的信息，在不同的几何尺度上研究就可能获得对不同量级损伤敏感的特征参量。基于非线性动力理论的损伤识别方既可以适用于线性系统，也可以适用于非线性系统。获得包含足够系统信息和维数尽可能低的吸引子对成功识别结构损伤至关重要。混沌振动信号具有宽频带和低维度的特点，非常适合用作结构系统的激励信号。混沌振动信号激励下的结构系统类似于混沌信号的“滤波器”，不同的结构状态对应不同的滤波参数。在不同的参数下，滤波后的混沌信号将表现出不同的吸引子几何特征。Badii等［4］首先发现经滤波器作用后的混沌信号会出现维数增加的现象。Nichols等［5］将该思想推广并应用于结构损伤识别中，以滤波后吸引子维数的变化作为损伤特征参量。

我们在前期研究工作中，利用混沌振动激励和吸引子李亚谱诺夫维数作特征参量研究了螺栓连接结构的结合面损伤识别问题，发现表征吸引子整体统计特性的维数在识别结合面小程度损伤时灵敏度较差［7-8］。本文通过分析吸引子的局部几何特性，提取出一种对结合面小程度损伤敏感的特征参量；设计了螺栓紧固悬臂梁结合面损伤识别实验，引入固定端结合面损伤，验证了特征参量的有效性；并进一步研究了计算参数取值不同对特征量的影响。

1 基于混沌激励的结构损伤识别方法原理

对于一个d自由度的结构与混沌激励F（x）耦合的动力学系统，其数学方程在状态空间中可表示为：

式中：z为一个d维的矢量，表示结构状态的响应（如位移、加速度等）。系数矩阵A包含结构的质量、刚度、阻尼等系统特性。系数矩阵B为输入x的耦合矩阵，包含激励输入的方向和作用位置等信息。这里假设结构与激励的耦合是单向的，即结构响应z不会对激励输入产生反馈影响。根据状态空间理论，式（1）所描述的耦合动力系统可认为是一个受滤波作用的混沌系统，其中的结构就像是一个“滤波器”，而混沌激励输入将会受到结构的滤波作用。结构损伤状态的变化将导致滤波器参数的变化，进而使得滤波后的混沌信号表现出不同的动力学特性。在状态空间中，吸引子是系统动态特性的反映，通过研究信号吸引子的几何变化特征，就可能对结构不同的损伤状态进行识别。

2 基于吸引子局部几何分析的特征参量提取

较为直接的方式是选取吸引子统计不变量，例如李亚谱诺夫指数、关联维数等作为特征参量。但是，研究表明，关联维数等统计不变量作为描述吸引子全局几何特性的特征量只能表征吸引子全局尺度上的特征变化，却无法表征由于小程度损伤引起的吸引子局部几何特性的变化。因此，为了提高特征参量对损伤的灵敏度，必须分析吸引子的局部几何结构，提取表征吸引子局部几何特性改变的新的特征参量。

为了研究吸引子局部尺度上的几何特性变化，本文引入了吸引子上某一点邻域内邻近点散布的改变来表征吸引子局部几何特性的变化，其基本思想是结构的损伤状态没有发生改变时，相同激励作用下获得的吸引子上邻域内邻近点的散布不会发生变化，反之邻近点的散布则改变。

本文通过计算邻域内邻近点的方差来定量描述邻近点散布的改变，并以此构造了一种表征结构损伤状态变化的特征参量，其具体计算步骤为：

（1）选取结构未损伤状态作为参考状态，对参考状态的响应时间序列，选取合适的延迟时间T和嵌入维数m重构出参考状态的吸引子，即：

（3）构造与每个基准点范氏距离最近的Nb个时间索引为tj（j=1…Nb）的邻近点组成的邻域。由于本文中所提取的特征参量表征的是吸引子局部几何特性的变化，应将时间相关的邻近点排除，故选择邻近点时不考虑距基准点一定时间窗长度［9］h内的邻近点。时间窗长度h可选为时间序列的自相关函数时间。从重构的响应吸引子中找到的第n个邻域可表示为：

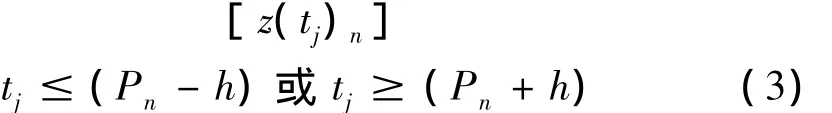
为方便起见，记为Zn。

（4）利用统计方法计算出每个邻域中Nb个邻近点所组成的样本的方差：

因为组成邻域的样本为多维数据，对于给定的邻域方差即为各维分量方差之和

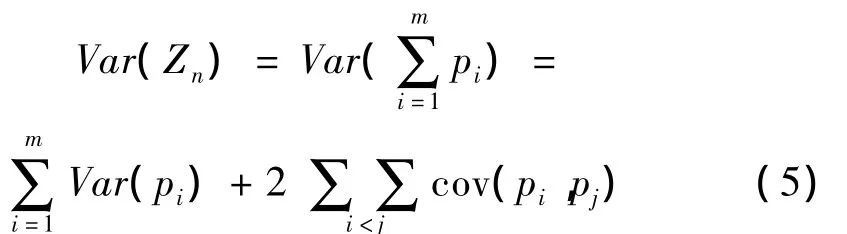
式中pi表示邻域中样本的某一维分量。

（5）将N个基准点的邻域方差求平均值即可获得平均吸引子局部方差：

记为ALAV（Averaged Local Attractor Variance），此值即为所要提取的表征结合面状态的特征参量值。

（6）利用步骤（1）中所用的延迟时间T和嵌入维数m值分别重构其他损伤状态下的响应吸引子，并利用步骤3中构造参考状态的N个邻域时所使用的邻近点时间索引tj分别构造其他损伤状态下的响应吸引子上与参考状态对应的N个邻域，再按照步骤（4）、步骤（5）分别计算出不同损伤状态下响应吸引子的ALAV。

比较不同损伤下的特征参量，就可以实现对结构损伤的识别。

需要说明的是，上述计算方法中，要保证各损伤状态的结构动力响应信号是在同一混沌激励信号作用下以相同的采样频率采集获得的时间序列，以使得各组数据点之间在时间上是同步关系。在重构响应吸引子过程中，各组时间序列应选取相同的延迟时间T和嵌入维数m。按照非线性动力学理论，嵌入维数的选取依据是保证重构吸引子在状态空间中完全打开，使重构的吸引子与原系统的动力学特性等价。然而，本文所构造的特征参量仅仅是利用了吸引子局部几何上的相对变化信息，故无需严格保证两者之间的动力学特性等价。为计算简单，嵌入维数m的选择可适当的取小些（实际可认为是利用了吸引子的投影信息）。延迟时间T的选择原则是使重构的状态矢量的各维分量之间具有某种程度的独立但又不完全无关，以便它们能在重构的相空间中作为独立的坐标处理。由于耦合系统是非线性混沌系统，可采用平均互信息法计算获得合适的延迟时间T以满足上面所述的两点要求［10］。

2 实验设计和方法

为了验证上文所述的理论和方法并将其应用于结合面损伤识别，设计了一套悬臂梁实验装置，在固定端连接结合面上引入螺栓紧固力下降的损伤。实验装置如图1所示。振动激励电压信号选用Lorenz混沌系统的第一个状态分量值，那么，式（1）可展开为：

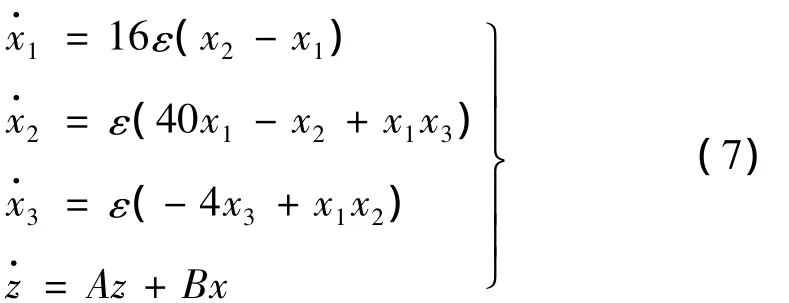
式中，参数ε用于调整Lorenz吸引子振荡速度的快慢，实际上相当于调整激励信号的能量频谱，使得激励与待测结构产生有效的动力耦合。悬臂梁材料为钢，尺寸为360 mm×100 mm×8 mm，固定端结合面部分长度为80 mm。激励信号采用四阶Runge-Kutta数值积分计算式（7）前三项获得，并由振动控制及数据采集系统中的NI PCI-6251数采卡转换为模拟电压信号后经由功率放大器输出给激振器。激振器作用于悬臂梁距自由端130mm处，其输出的激振力由一个CL-YD-312型压电式力传感器进行测量，测量信号先后经过阻抗交换器和恒流适调器进行信号调理后送入振动控制及数据采集系统。混沌振动激励下结构的加速度响应由三个CA-YD-1182型压电式加速度传感器测量获得。本实验中分别在悬臂梁自由端（ACH1），距离自由端130 mm（ACH2）以及280 mm（ACH3）处各安装一个加速度传感器。基于Lab/Windows CVI平台设计开发了本实验的振动控制及数据采集控制软件。

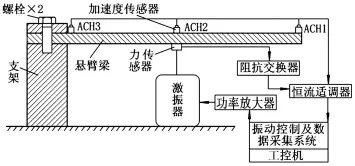
图1 实验装置图Fig.1 Experimental setup

实验过程中通过同步改变悬臂梁固定端2颗螺栓预紧力的大小来模拟结合面的损伤状态。取螺栓预紧力为额定值时为结构未损伤状态（参考状态），实验中通过力矩扳手给螺栓施加不同的力矩对螺栓预紧力进行调节。为保证螺栓预紧力的施加精度，每次实验前都重新对螺栓预紧力进行调节校准。本实验共选取五组典型连接状态，其中状态1为参考状态，其余四组作为损伤状态，如表1所示。

表1 结合面损伤状态Tab.1 Description of damage cases used in the experiment

经比较，实验时选取参数ε=10，采样频率设为1 kHz，每通道采集长度为10 000个数据点。对于每种结合面状态，在相同激励作用下重复实验各采集四组稳态条件下的加速度响应值。通过对加速度响应的相空间重构，计算分析五种典型状态下ALAV的变化。

3 结果分析与讨论

3.1 特征参量的有效性

选取结合面状态1的加速度响应时间序列为参考状态，利用平均互信息函数法计算获得参考状态响应时间序列的延迟时间T=4，由自相关函数计算获得时间窗长度h=37，为计算方便嵌入维数取m=2。利用上述参数，依据3中所述的特征参量提取方法分别对各个状态下各通道的加速度响应时间序列进行相空间重构，计算取N=1 000，Nb=20时各组加速度响应的特征参量ALAV，并选取每个通道各组ALAV的平均值作为识别该状态的特征参量。实验中混沌激励电压、激振力及加速度的典型时间响应历程曲线如图2所示。

各通道在不同状态下的ALAV变化曲线如图3～图5所示。由图可知，以结合面状态1为参考状态，其它四种状态的ALAV在相同激励作用下相对于参考状态都发生了明显的改变，即随着结合面螺栓预紧力的减小，加速度响应的 ALAV单调增大，故特征参量ALAV能够表征并区分不同的损伤状态，可应用于结合面状态的识别。三个通道相比较可知，ALAV的变化程度并不一样，ACH1的ALAV变化最大，ACH3的ALAV变化最小，说明相比与其他通道，ACH1对于结合面的损伤状态的变化更敏感，且ACH1各状态的ALAV实验值散布最小，计算值较稳定，而ACH2状态2、3、4和ACH3状态3、4、5的ALAV实验值散布较大，各状态的离散实验值之间还出现了交叉重叠现象，这将降低了ALAV对结合面状态的灵敏度，不利于有效区分结合面的状态。出现上述结果的主要原因是通道1位于悬臂梁动响应幅值最大处，响应时间序列的信噪比较好，受噪声等干扰的影响少，故计算特征参量的灵敏度和散布特性都较好。ACH2通道响应受激励影响，而ACH3通道动响应值太小，都不离于特征参量计算。因此，响应测点的配置对特征参量的敏感度、计算精度都有影响。

图2 参考状态下的典型时间历程曲线Fig.2 Representative time series from a test in the baseline damage condition

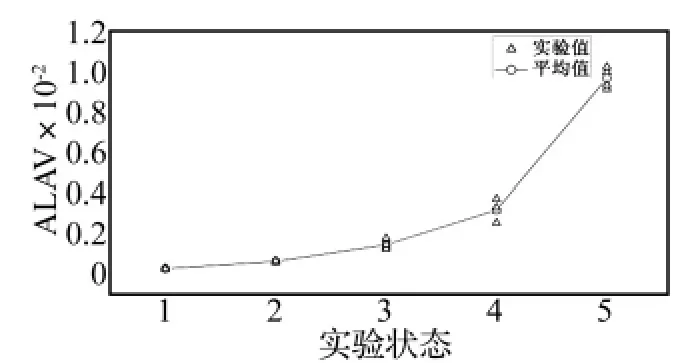
图3 不同状态下ACH1的ALAV变化曲线Fig.3 ALAV values of ACH1 at each damage condition

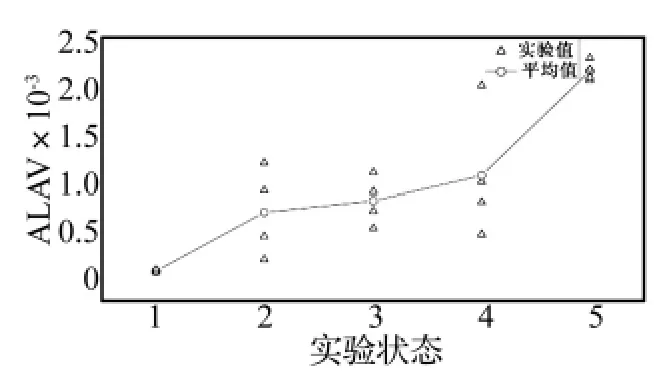
图4 不同状态下ACH2的ALAV变化曲线Fig.4 ALAV values of ACH2 at each damage condition

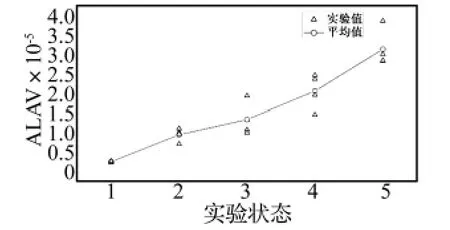
图5 不同状态下ACH3的ALAV变化曲线Fig.5 ALAV values of ACH3 at each damage condition

4.2 参数N、Nb对损伤识别的影响

特征参量计算时，基准点数N和邻近点数Nb是重要的影响参数。选取4.1中实验值散布性较好的ACH1的响应时间序列进行参数影响分析，分别计算Nb=20，N取 500、1 000、2 000、3 000、4 000 和N=1 000，Nb取 10、15、20、25、30 两类情况下响应的ALAV，并取每种结合面状态下的四组实验数据的ALAV平均值作为该状态的ALAV，利用参考状态的ALAV值对各状态的特征参量值进行正则化处理。

图6 为Nb=20，N取500、1 000、2 000、3 000、4 000时正则化ALAV的变化曲线。从图中可知，当邻近点个数Nb取20时，随着基准点数N的变化，各状态的正则化ALAV值的变化很小，即基准点数目的变化对特征参量的计算结果影响较小。随着结合面损伤状态的变化，正则化ALAV值的变化规律基本不变，未改变ALAV随紧固预紧力的减小而单调增大的趋势，这表明基准点数目的选取对特征参量的影响很小，在大批量的数据计算过程中N可取总数据量的10%左右。

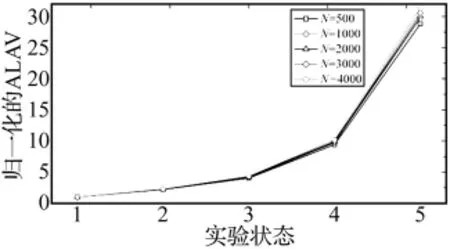
图6 取不同基准点数N时ACH1的正则化ALAV变化曲线Fig.6 Normalized ALAV values of ACH1 with different fiducial point number N

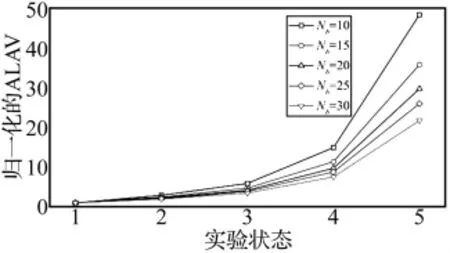
图7 取不同邻近点数Nb时ACH1的正则化ALAV变化曲线Fig.7 Normalized ALAV values of ACH1 with different nearest neighbors number Nb

图7 为N=1 000，Nb取 10、15、20、25、30 时正则化ALAV的变化曲线。从图中可知，在相同状态下，随着邻近点数目Nb的增加，正则化ALAV值变小，这是因为随着邻近点数目的增加，基准点邻域样本增加，邻域在空间中的区域变大，邻域的局部方差值会有所增大，但这里参考状态的方差值增加幅度大于其它几种状态，故正则化ALAV值变小。此外，通过比较不同邻近点数时ALAV的变化曲线可知，当邻近点数目逐渐增大时，特征参量ALAV随状态变化的曲线将趋平，从而失去区分损伤状态的能力。显然，邻近点数达到一定比例时，特征参量将反映的吸引子的全局几何特性。考虑到计算量等因素，邻近点数目可取为总数据量的1‰～3‰。

4 结论

本文研究了基于混沌振动激励和吸引子局部几何特性分析的结合面损伤识别方法，提取了基于吸引子局部方差的特征参量，并设计了悬臂梁结合面损伤状态识别实验进行了实验验证。研究结果表明：

（1）本文的方法和所构造的基于吸引子局部方差的特征参量，可以表征吸引子的局部几何特征的变化，能够有效地识别出结合面的损伤状态。

（2）响应测点配置不同对特征参量的灵敏度和计算精度有影响，应选择响应幅值较大的点作为观测点。

（3）在一定范围内，基准点个数的选择对特征参量的识别结果和灵敏度影响较小。

（4）邻近点个数的选择对特征参量的识别结果和灵敏度有较大影响，应合理选择。

进一步的研究可考虑应用反馈控制提高实验的精度，并进一步研究吸引子的精细结构，以构造灵敏度更好的损伤特征量。

［1］ Yan Y J，Cheng L，Wu Z Y，et al.Development in vibration-based structural damage detection technique［J］.Mechanical Systems and Signal Processing，2007，21：2198-2211.

［2］ Todd M D，Nichols J M，Nichols C J，et al.An assessment of modal property effectiveness in detecting bolted joint degradation：theory and experiment［J］.Journal of Sound and Vibration，2004，275：1113-1126.

［3］ Worden K，Farrar C R，Haywood J，et al.A review of nonlinear dynamics applications to structural health monitoring［J］.Structural Control and Health Monitoring，2008，15：540-567.

［4］ Badii R，Broggi G，Dertghetti B，et al.Dimension increase in filtered chaotic signals ［J］.Physical Review Letters，1988，60（11）：979-982.

［5］Nichols J M，Virgin L N，Todd M D，et al.On the use of attractor dimension as a feature in structural health monitoring［J］.Mechanical Systems and Signal Processing，2003，17（6）：1305-1320.

［6］Ryue J，White P R.The detection of cracks in beams using chaotic excitations［J］.Journal of Sound and Vibration，2007，307：627-638.

［7］裘群海，张振军，徐 超.一种采用混沌振动信号激励识别连接状态的方法［J］.振动与冲击，2010，29（s）：13-15.

［8］Qiu Q H，Xu C，Wu B.Structural damage detection through chaotic interrogation and attractor analysis［J］.Advanced Materials Research，2011，163-167：2515-2520.

［9］ Theiler J.Spurious dimension from correlation algorithms applied to limited time-series data［J］.Physical Review A，1986，34（3）：2427-2432.

［10］ Kantz H，Schreiber T.Nonlinear time series analysis［M］.Cambridge：Cambridge University Press，2002.