囊式混合介质隔振器的动力学特性试验

张树桢，陈 前，滕汉东

（南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016）

气囊（又名空气弹簧，气胎）是一种性能优良的隔振元件，将其应用于船舶上，可以有效地隔离舰艇动力机械的振动。随着技术的发展，气囊隔振器的性能进一步完善，目前基于压缩气体的隔振器已经广泛应用于车辆、重型机械乃至大型喷气飞机的结构设计中。

在船舶中使用气囊的优势在于：① 气囊刚度低，随主机的激励对内部气体产生较大压缩，可有效的减小传递率；② 随气囊振动的增大，引起气囊内气体体积的往复变化和外壳的往复变形，气囊内气体和外壳的内阻尼也会吸收一部分振动能量，这大大的超过了传统的隔振器的隔振效果；③ 由于压缩气体的非线性刚度，气囊隔振系统的固有频率基本不变［1］。但在气囊的实际应用中也存在严重的缺陷。由于气体非常稀薄，气体分子间隙较大，因而易于穿过橡胶基的囊容器壁而导致泄漏，而且内压越高，气体泄漏速度也会随之增大。气囊隔振器可以承受较重的负载，但承受不同负载的气囊囊体结构基本相同，所以承受大负载的气囊隔振器，气体泄漏问题更加突出。气体的压力虽可以利用舰艇内的压缩气体系统检测、调整并保持，但附加监测与控制设备使得本来简单的被动隔振系统变得更复杂。而对中小型船舶或其它轻型设备而言，建立独立的气囊稳压系统成本高昂。

本文采取在囊容器内部填充可弹性变形的波纹管单元体并以水或者液压油为介质替换压缩气体组成囊式混合介质隔振器，这样既可以解决气囊的泄漏问题，又可免去附加的监测系统和气体压缩机设备所占据的空间和消耗的动力。该研究的目的在于：研究分析囊式混合介质隔振器的非线性动力学特性在隔振减振方面的作用，试验分析得到囊式混合介质隔振器的刚度特点以及对重型负载的隔振效果。

1 囊式混合介质隔振器的动力学特性理论分析

本文以某型单曲气囊隔振器为容器，将其内部分别填充①高压气体；②波纹管单元体和液体所组成的液固混合介质，并进行研究分析。由图1所示的囊式混合介质隔振器示意图可见，将囊式空气弹簧作为囊容器，内部填充波纹管单元体和液体。在承受负载的情况下，囊容器内部液体压强发生改变，由液体将均布压强传递至波纹管，从而使波纹管单元体产生相同的变形。利用该理想受力条件，推导混合介质隔振器的刚度并进行试验研究。

本节主要工作是运用波纹管单元体在外部水压作用下的轴向刚度理论和囊体变形的几何关系，推导囊容器填充波纹管单元体和液体后组成的混合介质隔振器的轴向刚度公式，分析囊容器的有效面积、内压力和波纹管单元体刚度等参数在刚度中所起的作用。

分析填充混合介质后囊容器的轴向刚度：

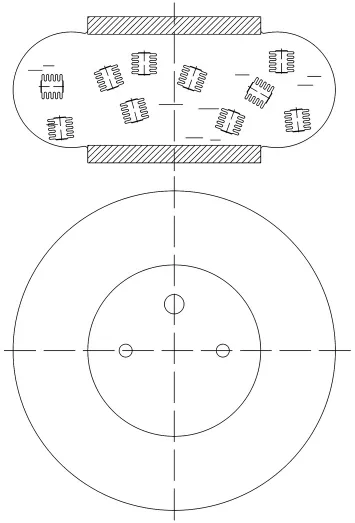
图1 囊式混合介质隔振器示意图Fig.1 The sketch of SALiM medium of vibration isolator

式中：F为囊容器上下金属板作用力；p为囊容器表压；Aeff为囊容器有效承载面积（变量）。

式中：ΔV为波纹管单元体体积变化量；Δx为波纹管单元体高度变形量；a为波纹管单元体有效面积；

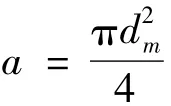
dm为波纹管单元体的有效直径，为其内径、外径之和的一半。

由于囊容器的帘层材料强度高，正常工作状态下囊容器体积变化量较小，可设囊容器的体积变化量ΔV总为波纹管单元体的体积变化总量，得到囊容器的体积变化量表达式：

式中：n为波纹管单元体数量；

囊容器的高度变化量Δz和体积变化量的关系为：

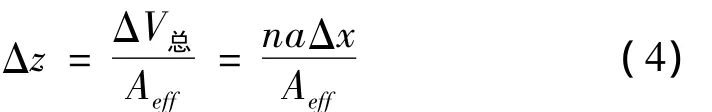
将（4）式化简得到波纹管单元体高度变形量Δx：

单个波纹管单元体受到的作用力f为：

Δp为波纹管单元体内外压力差。

由囊容器内外作用力平衡状态，有：

式中：p0为大气压强；pi为波纹管单元体的内压；pj为囊容器内压。

对（7）式求导有：

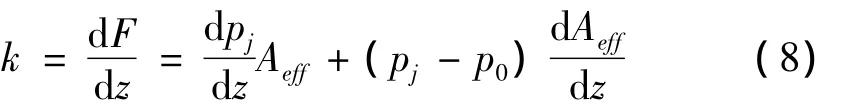
利用曲梁模型［2］，考虑波纹管单元体内外压差的作用并对刚度方程进行线性优化得到［3］：

式中：为波纹管单元体在外部水压作用下的轴向刚度；kp为等效真空波纹管单元体轴向刚度，只与波纹管单元体的波数、壁厚和内径等几何参数有关；

式中：n1为波纹管单元体波数；EI为抗弯刚度；l为波高；d为内径；h为波纹管单元体比例系数。

pi的表达式为：

式中：l1为波纹管单元体在空气中的原长度；y1为放置于液体中的压缩量；

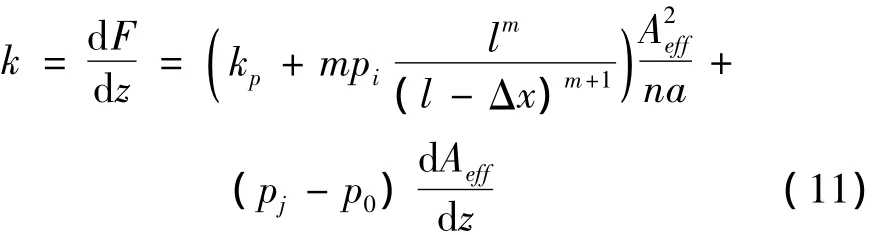
囊容器以气体为介质的轴向刚度表达式为［4］：

式中：m为多变指数，静态为1，动态为1.4（经验函数）。当振动缓慢时，气体状态的变化接近于等温过程，取m=1；当振动激烈，气体状态的变化接近于绝热过程，取m=1.4。在一般情况下，m=1.3 ～1.38［5］；p为囊容器内压；p0为标准大气压；Aeff为有效面积。

2 囊容器试验装置及试验方法

以某型囊容器和波纹管单元体作为试验对象，测试囊式混合介质隔振器的动力学性能。试验装置如图2（a）所示，囊容器安装在负载质量和两对边固支的基础薄板之间，负载质量通过连杆和激振器连接。其中阻抗头安装在连杆和激振器之间，加速度传感器安装在基础板上。35 670动态信号分析仪生成正弦扫频的电压信号经功率放大器输入到激振器中，以产生作用力。由阻抗头将测量到的力和负载质量的上部加速度信号输入35 670动态信号分析仪分析出系统的加速度原点频响。利用阻抗头处的上部加速度信号和基础板处的下部加速度信号的比值确定系统的振级落差。由船舶主机的工作频率范围确定线性变化的扫频频率范围为1～50 Hz，同时由于分析对象的不同，扫频范围会有区别，比如在分析共振点时，取3～8 Hz分析，以达到提高精度的目的。

按照图2所示条件进行动力学特性试验，对激振器输入正弦扫频信号，将通过阻抗头和加速度传感器采集的加速度和力试验数据，输入到35 670信号分析仪中，分析囊式混合介质隔振器的刚度特点和隔振效果。

① 囊容器填充气体3bar，进行不同幅值水平的激励；② （2-1）囊容器分别填充30、50、80个波纹管单元体，并充以高压液体（表压）3bar，进行不同幅值水平的激励；③ （2-2）针对填充80个波纹管单元体的囊容器，分别进行液体压强为2bar、3bar及4bar情况下相同幅值水平的激励。

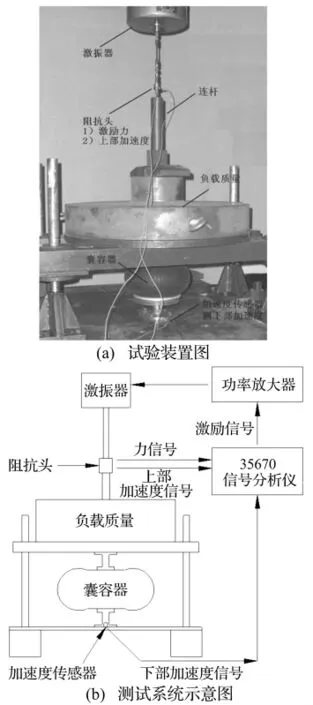
图2 试验结构图Fig.2 The structure of test system

3 试验结果与分析

3.1 工况（1）囊容器填充气体

图3、图4为囊容器在内部填充3 bar压强气体的情况下的频响曲线，通过多项式拟合的方法分析由图3所示的共振点为3.558 2 Hz与图4所示的共振点3.567 4 Hz基本一致。但由图4可见频响曲线在低频段3 Hz左右存在着凸起，这是由该处加速度突变导致的。主要原因是气囊在低频振动过程中，存在着径向刚度不足的缺陷，当位移量较大，容易失去稳定性，从而导致测量的加速度曲线不平滑，参考文献［8］中实测的频响曲线存在同样的情况，所以当使用填充气体的气囊时，需要多个气囊组成隔振系统以及限位器，防止发生较大的径向晃动。

3.2 工况（2）囊容器混合介质隔振器

以填充80个波纹管单元体的囊式混合介质隔振器作为主要分析对象。

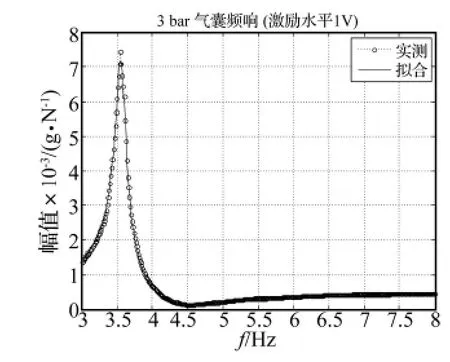
图3 3bar气囊频响曲线Fig.3 3bar frequency response curve

图4 3bar气囊存在径向刚度不足的频响曲线Fig.4 3bar frequency response curve of insufficiently radial stiffness

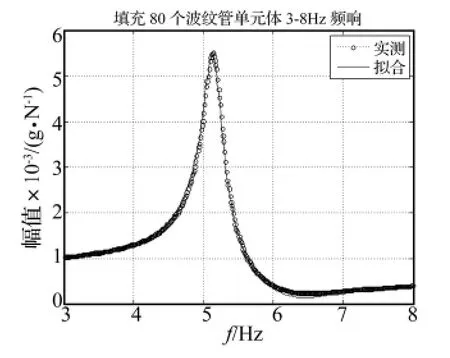
图5 囊式混合介质隔振器3～8 Hz频响曲线Fig.5 3 ～8 Hz frequency response curve

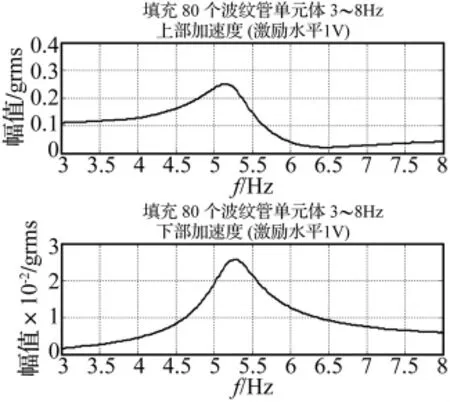
图6 囊式混合介质隔振器加速度谱Fig.6 Acceleration linear spectrum of isolation

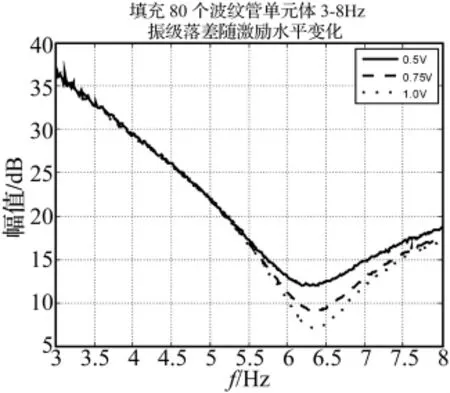
图7 3～8 Hz振级落差和激励水平的关系Fig.7 3 ～8Hz vibration level difference under different stimulation level

图8 3～8 Hz频响曲线和激励水平Fig.8 3 ～8 Hz frequency response under different stimulation level

表1 囊式混合介质隔振器各频率点分布情况 （单位：Hz）Tab.1 The situation of frequence point

由图5可见在该压力条件下囊式混合介质隔振器的共振点为5.138 0 Hz，较以气体为填充介质的工况（1），其固有频率发生了较大的改变，原因在于混合介质隔振器中填充液体和波纹管单元体后，囊容器受到作用力，介质被压缩，体现了波纹管的刚度作用。评价隔振器隔振效果的指标很多，目前采用得较多的有：力传递率、振级落差、插入损失和功率流方法。文献［9］对前三种方法进行了比较研究。适用于柔性基础隔振效果评估的方法是振级落差与功率流传递率，由于振级落差测量较为方便实用，因而大多数的船舶动力机械隔振系统的实际效果评估多采用振级落差作为评价标准，本文即以振级落差作为评价标准。振级落差分为速度振级落差和加速度振级落差，如果为简谐激励，其振级落差数值结果一致。设：

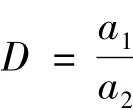
式中：a1为阻抗头处加速度（上部加速度）；a2为基础板处加速度（下部加速度）；

振级落差的表达式为：LD=20lg（D）。

由图7可见在6.337 5 Hz时，三条振级落差曲线均达到了最低点11.974 4 dB、9.061 5 dB、7.079 3 dB。这表明在相同填充数量的条件下，激励力幅值的变化只在下降区域有明显差别，而且激励电压越大（作用力越大），下降越剧烈。该最低点主要与图6中的上部加速度线性谱在6.337 5 Hz处存在最低点有关。在共振点5.138 0 Hz处的振级落差分别为 20.679 1 dB、20.567 7 dB、20.484 5 dB，效果良好。

由图8及表1可以看出：① 在不同激励幅值下隔振系统的共振点均为5.13 Hz，表现出线性系统的特点，意味着在小振幅情况下，系统的非线性特性不明显；② 频响函数曲线的最低点对应上部加速度响应曲线的最低点，位于6.462 5 Hz，上部加速度响应曲线在共振的峰值点后存在的波谷，意味着激振器输入到质量块处向下的作用力和质量块受到的隔振器向上的作用力，数值大小基本一致，导致加速度下降。表明该试验台架和隔振器组成的隔振系统存在反共振现象；③振级落差的最低点，位于上部加速度最低点之前，该处的下部加速度有相对较大值，所以振级落差在该处有低谷。产生低谷的原因在于使用的试验工装夹具结构所产生的影响，并不是隔振器的固有属性，实际所使用的隔振器不存在类似的谷值。

图9所示在填充数量相同的前提下，在高频段不同的激励力幅值所得到的振级落差的数值稳定在25dB，表明混合介质隔振器的隔振性能稳定。

图9 振级落差和激励水平的关系Fig.9 Vibration level difference under different stimulation level

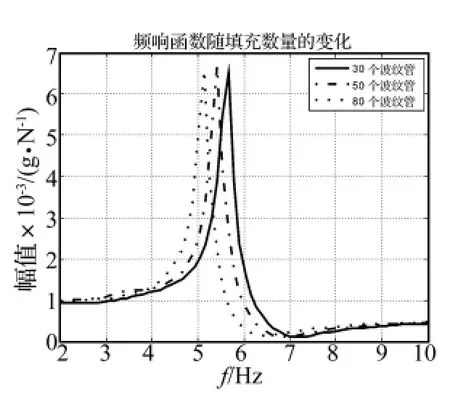
图10 频响函数曲线和填充数量的关系Fig.10 Frequency response under different quantity

图11 振级落差和填充数量的关系Fig.11 Vibration level difference under different quantity

由图10、图11可见随填充数量的增加，频响函数曲线的峰值点向低频段迁移，固有频率（5.2 Hz、5.45 Hz、5.7 Hz）随填充数量的增加而降低，系统的刚度随之降低。而且随填充数量的增加，在相同的激励力条件下，振级落差的数值随填充数量的增加而增大，表明填充数量的增多，对系统隔振效果的提高具有积极的作用。

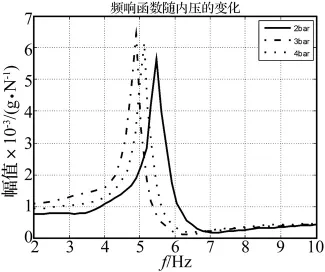
图12 内压和频响曲线的关系Fig.12 Frequency response under different pressure

同时，振级落差曲线的最低点随填充数量的增加而向低频段迁移，其主要原因在于上部加速度线性谱的谷值向低频段迁移。进一步分析得出随填充数量增加，波纹管单元体对刚度的贡献量变大，系统的固有频率降低，刚度下降。在相同激励水平下，随填充数量的增加，振级落差曲线最低点的数值，逐渐变大，表明囊式混合介质隔振器的性能在各个频率段都随着波纹管单元体数量的增加而改善。图13分别为填充2 bar、3 bar和4 bar混合介质的囊容器和3 bar空气的囊容器的振级落差曲线，图13与图9比较，随着系统刚度的提高，其振级落差的数值在高频段降低。对比分析工作压强2 bar、3 bar和4 bar的情况，得出在高频段3 bar的隔振效果最好，达25 dB以上。

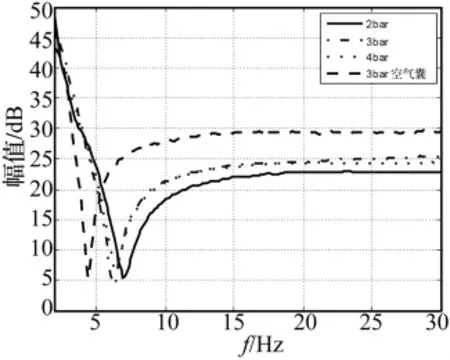
图13 内压和振级落差的关系Fig.13 Vibration level difference under different pressure

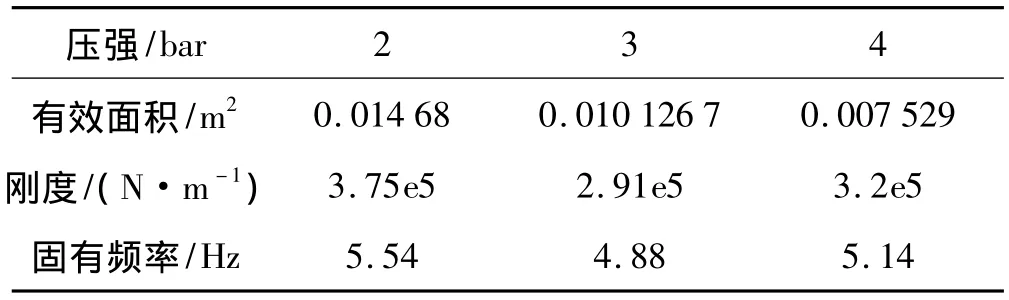
表2 不同压强条件下的试验结果Tab.2 Test results under different pressure

同时由图13可见，在相同的内压条件下，填充混合介质的囊容器的振级落差曲线较填充气体的曲线低，说明填充混合介质后的隔振效果存在一定程度的下降。

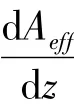
4 结论

本文通过计算分析和振动试验研究了囊式混合介质隔振器的动力学特性，得出以下结论：

（1）解决了囊容器在以气体为填充介质时的泄漏的问题。在试验过程中，填充气体的囊容器，压力越大，泄漏量越大。填充混合介质，在相同的压力条件下，经过相同的时间，其压力读数不变，频响结果无变化。囊容器在实际使用中泄漏难以控制，须配套相应的气体压缩机、测压和控制装置，导致气囊隔振系统成本的提高和重量的增加，同时也加大了设计难度。填以波纹管单元体和液体为介质后解决了泄漏问题，对系统配套的高度监测系统和压力稳定设备要求降低，大大降低了应用成本和设计的复杂性。

（2）从图4及相关文献得到填充高压气体的囊容器，由于径向刚度不足，导致在大位移情况下容易失稳。而且由于填充气体和负载的同步变化，理论上导致其固有频率稳定不变，从而导致失稳的问题普遍存在，而囊式混合介质隔振器的径向稳定性则较好。由于刚度较低，在高频段填充气体的囊容器的隔振效果是优于填充混合介质囊容器的。

（3）囊容器的刚度随填充波纹管单元体数量的增加而降低；随填充液体压强的变化则呈现较为复杂的规律：囊容器内压较小，则有效面积较大，导致其刚度较高；当内压较大，则有效面积减小，由内压的增大导致刚度提高。这表明填充波纹管单元体后，在高度不变的前提下，囊容器的刚度可调范围大且方式灵活多样。

［1］楼京俊，朱石坚.空气弹簧特性研究［J］.噪声与振动控制，2000，20（5）：18-20.

［2］黎廷新.U形膨胀节的轴向位移应力和轴向刚度［J］.油设备设计，1981，（3）：9-8.

［3］高 雪，陈 前，滕汉东.波纹管式隔振单元体的刚度特性分析［J］.振动工程学报，2011，（5）：280-286.

［4］Homeyer A，瞿蓓兰.采用现代方法设计空气弹簧系统［J］.国外铁道车辆，1999，36（3）：35-38.

［5］刘文波.空气弹簧力学特性的有限元分析［D］.武汉：武汉理工大学，2006.

［6］郭荣生.206KP型转向架空气弹簧结构的研究［J］.铁道车辆，1995，12：142-147.

［7］朱若燕，李厚民，黄映云.圆筒形囊式隔振器静态和动态特性研究［J］.工具技术，2006，40（11）：23-26.

［8］徐 伟，何 琳，杜兴业.空气弹簧系统动态性能研究［J］.噪声与振动控制，2005，25（1）：5-6，28.

［9］朱石坚，何 琳.船舶机械振动控制［M］.北京：国防工业出版社，2006.

［10］陈大荣.船舶柴油机设计［M］.北京：国防工业出版社，1980.

［11］ Toyofuku K.Study on dynamic characteristic analysis of air spring with auxiliary chamber［J］.JSAE Review，1999，（3）：349-355.