基于假设模态法的风力机动力学分析
2012-02-13何玉林
王 磊,陈 柳,何玉林,刘 桦,金 鑫
(1.电子科技大学 能源科学与工程学院,成都 611731;2.重庆大学 机械学院,重庆 400044)
水平轴风力发电机系统作为具有强非线性流固耦合特性的周期时变动力学系统,其结构特征及其运动较为复杂。风在风力发电机组部件上产生的气动载荷与部件的变形之间相互作用,使风力发电机组系统具有气弹耦合现象,系统柔性增加使各部件之间的运动和受力相互耦合更加显著,解决这种柔性较大的系统的动力学问题,需要采用柔体动力学方法。近几年来,国内外许多学者对风力发电机组的动力学进行了研究:文献[1]利用有限元法研究了桨叶、耦合转子/机舱、塔筒系统的动力响应。文献[2]研究了风机气动性能和结构动力学特性,建立了桨叶半刚性模型。文献[3]根据Hamilton原理推导了10自由度梁单元离散桨叶的运动方程。文献[4]使用假设模态方法研究旋转运动柔性梁动力特性,并通过与有限元离散化方法比较发现高速运动的系统,需要增加模态数目来降低误差。
采用Kane方法[4-6]建立的风力机多刚体系统动力学模型,依据假设模态法进行离散化,并结合修正的BEM模型进行轴向诱导因子a过渡点修正,进行空气动力载荷计算气动力模型,建立风力发电机组整机系统动力学模型。以某2.5 MW风力发电机组为例,进行数值仿真计算,并对风力发电机组在随机风场下的动力学运动规律以及动力学特性进行分析。
1 风力机多刚体系统动力学模型
文中采用Kane方法建立风力机多刚体系统动力学模型。首先确定以塔筒底部中心为原点中心,垂直于风轮平面的来流方向X方向,塔筒未变形时的中线方向为Z向的惯性坐标系E,如图1所示。
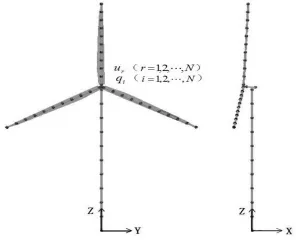
图1 三叶片风力机系统模型Fig.1 The model of three-bladed wind turbine
将风力发电机组视为具有N个自由度的一阶线性多刚体系统,则风力机系统的运动可以由N个广义坐标qi(i=1,2,…,N)描述,或可由N个广义速率ur(r=1,2,…,N)描述。后者是从组成系统的质点速度或刚体角速度的中任意选择的N个独立标量,表示为广义坐标的导数的线性组合。
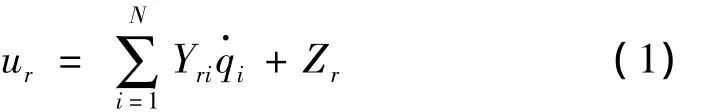
其中Yri、Zr为广义坐标qi和时间t的函数,若ur为独立变量,可以从方程(1)唯一的解出,得到:
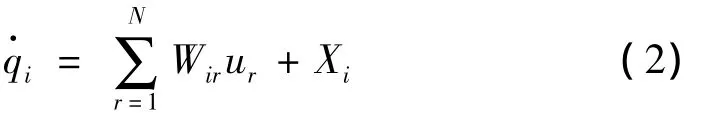
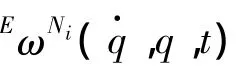
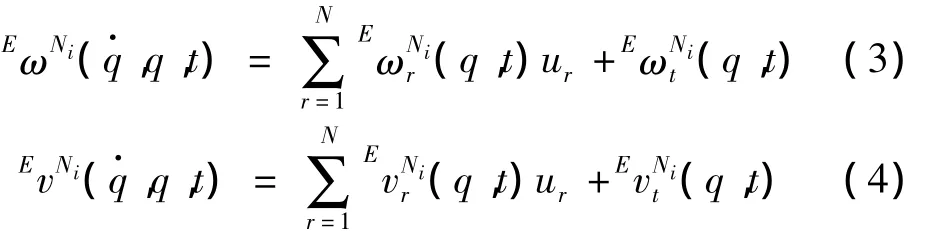
当确定了每个刚体的偏速度和偏角速度,以及相应的广义主动力Fr和广义惯性力之后,其Kane动力学方程为:
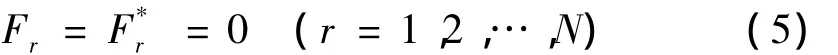
即每个广义速率对应的广义主动力和广义惯性力之和等于零。设风力发电机组系统由w个刚体组成。假设对于每一个刚体Ni,主动力施加在其质心Xi和分别为作用在作用在每个刚体Ni上的主动力与力矩,则风力发电机组系统的广义主动力为:
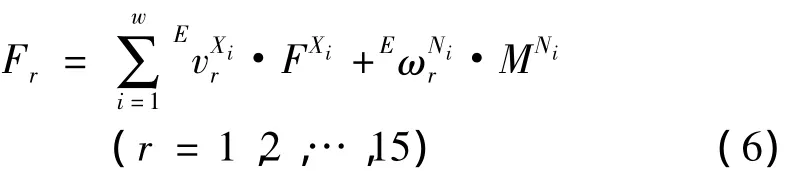
对应的广义惯性力为:
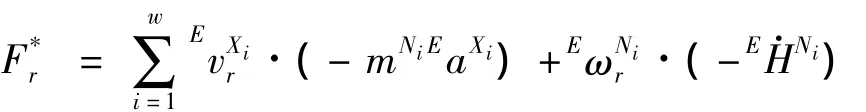

其中:
将式(6)、式(7)带入式(5),风力发电机组系统动力学方程矩阵形式则为:
其中的[C(q,t)]为系统加速度的系数矩阵,{f(,q,t)}为系统位移和速度相关的向量。求解时,在每个时间步,方程的数值解的第一步是采用四阶Adams-Beshforth预测-修正算法的预测方法确定低阶项的值,并以此以构成方程的右边项,然后采用Gauss消元法求解系统自由度的加速度,这些计算得到加速度值用于修正预测值,以提高预测精度。经过几次迭代后,采用四阶Adams-Mounton预测-修正算法的修正方法确定加速度的值,并给出该时间步的最终解。由于该预测-修正算法不是自发的,前四个时间步的解需要用四阶Runge-Kutta法确定。
2 基于假设模态法的风力机动力学模型离散化
将风力机叶片和塔筒视为质量和刚度连续分布的柔性悬臂梁。根据连续力学理论,该结构体具有无限多的自由度,因此需要无限多个坐标确定叶片和塔筒的每一个点的位置。但在假设模态法中,叶片和塔筒的连续体的变形被表示为一系列规格化的振动模态的振型线性叠加[7-8]。这样可以将叶片和塔筒的自由度从无限大减小为N(N表示计算时,选取的假设模态数目)。因此,柔性悬臂梁(叶片和塔筒)在任意时间、任意位置的横向变形u(z,t)是一系列规格化模态振型φa(z)的线性叠加,它们与广义坐标qa(t)的关系为:
其中:φa(z)是为悬臂梁的第a个模态振型,它是悬臂梁纵向方向上的距离z的函数;而与模态a相关的广义坐标qa(t)是时间的函数,它通常被取为该模态振型的悬臂梁自由端的变形。
采用保守的、不随时间变化的系统的Lagrange方程,一个N个自由度系统的运动方程为:
其中的cb(t)是关于形函数φb(z)的广义坐标;广义质量mij和广义刚度kij分别由动能T和势能V定义为:
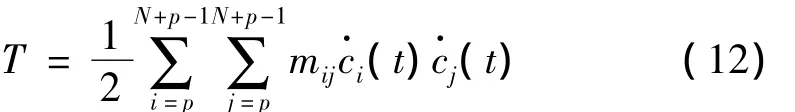
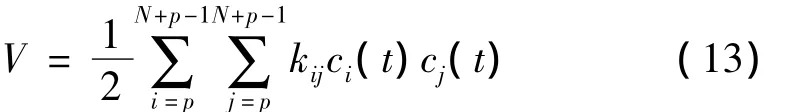
当悬臂梁以特定的固有频率ωa振动时,假设a=m,有:
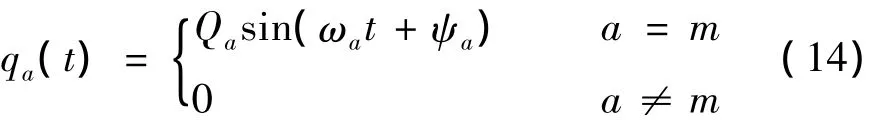
其中的Qa是悬臂梁的自由端部在自由模态a时的变形大小。将qa(t)代入方程cb(t)=Cm,bqm(t),并将得到的结果代入方程(2),得到:
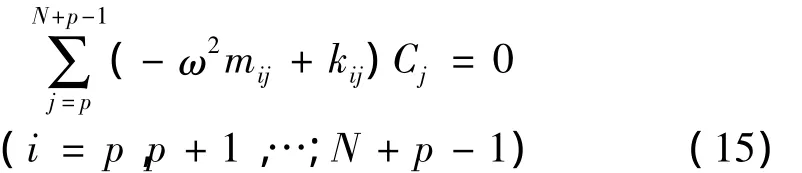
改写成矩阵形式为:
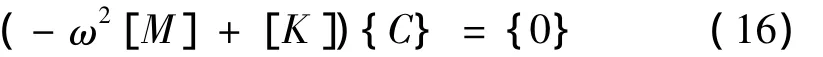
其中,广义质量矩阵[M]和广义刚度矩阵[K]都是N×N阶矩阵,系数向量{C}为N×1阶向量。对该矩阵方程进行特征值分析,得到特征值和特征向量{C}a。
2.1 塔筒的广义质量与广义刚度
塔筒被模拟为一个倒立的悬臂梁,它的自由端固定着一个点质量Mtop,表示基座盘、机舱、轮毂和叶片的总质量。塔筒的广义质量表示为:
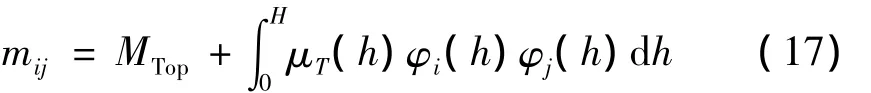
其中μT(h)是塔筒的质量分布线密度。
塔筒的势能由与梁的分布刚度有关的分量VBeam和与重力有关的分量VGravity组成:
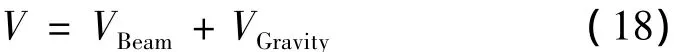
其中与梁的分布刚度相关的势能分量为:
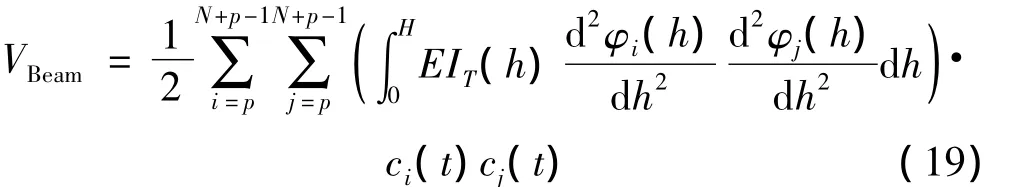
其中的EIT(h)是塔筒的分布刚度,H是塔筒的高度。
与重力相关的势能分量为:
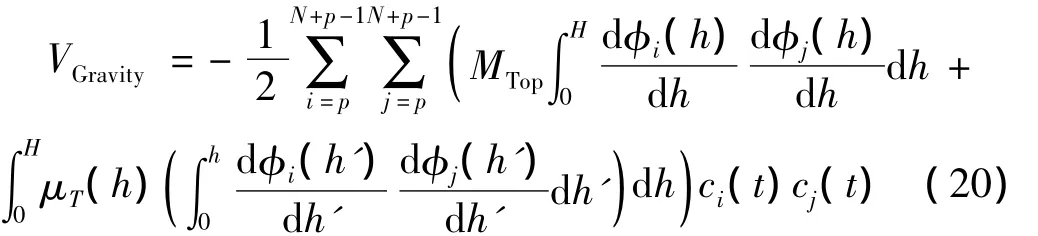
其中负号表示重力将减小塔筒的广义刚度,括号内的第一项与塔顶质量的重力有关,第二项与塔筒分布质量的重力有关,并考虑了塔筒变形对重力势能的影响。
与方程(4)比较并整理后,得到塔筒的广义刚度为:
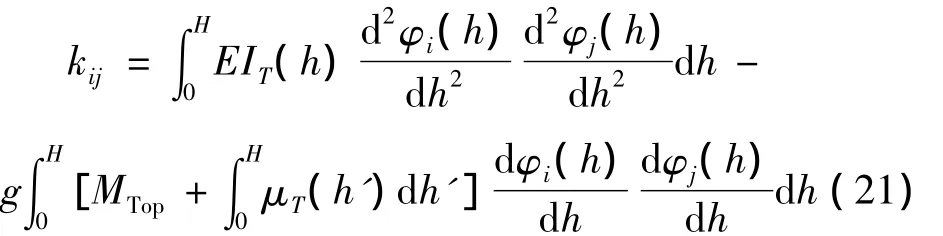
2.2 叶片的广义质量与刚度
风轮的每个叶片被模拟成自由端处固定一个点质量MTip的旋转悬臂梁,以角速度Ω绕垂直于风轮平面的轴旋转。假设每个叶片的柔性部分独立地向叶片的拍动方向(垂直于翼型弦线)和挥舞方向(平行于翼型弦线)运动。同时,叶片的变形也可以表示为面内方向(平行于风轮旋转平面)和面外方面(垂直于风轮旋转平面)的变形运动,拍动-挥舞与面内-面外两个坐标系之间的关系如图2所示。
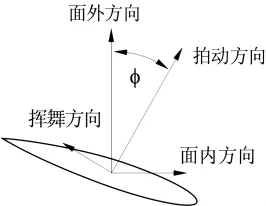
图2 拍动-挥舞坐标系和面内-面外坐标系Fig.2 Relationship between the flapwise-edgewise frame and inplane-out-of-plane frame
在随风轮旋转的坐标系中,叶片的动能与塔筒的动能的形式是一致的,叶片的广义质量可以写为如下的形式:
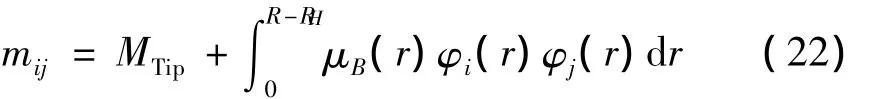
其中,μB(r)叶片的分布线密度,R是风轮半径,RH是轮毂半径。
忽略重力,叶片的势能由与叶片分布刚度有关的分量VBeam和与叶片旋转产生的离心力作用相关的分量VRot组成:

与梁的分布刚度相关的叶片势能分量为:
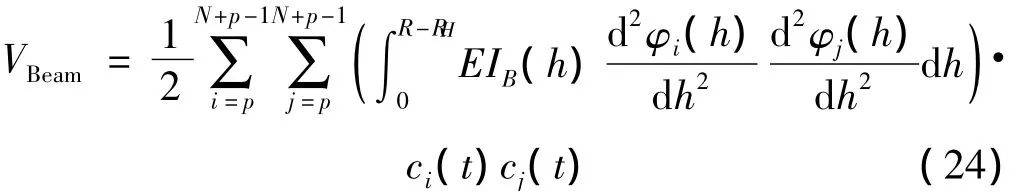
其中的EIB(h)是叶片的拍打方向或挥舞方向的分布刚度。
由风轮旋转引起的势能分量为:
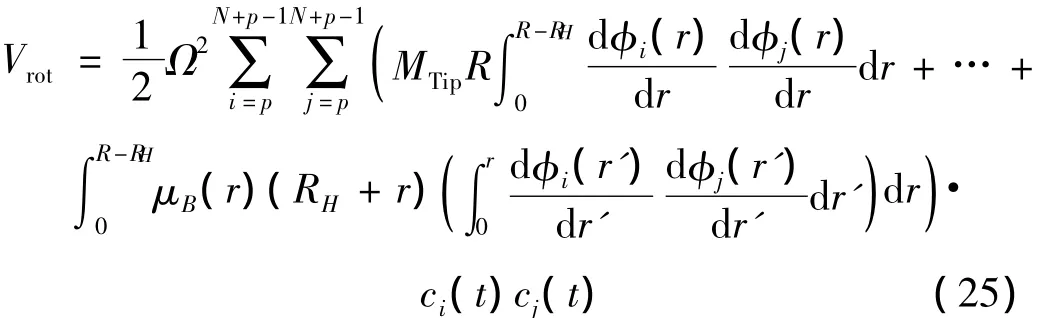
括号内的第一项是与叶尖刹车部分质量相关的势能分量,第二项是与叶片分布质量相关的势能分量。两者的离心势能之和取正值,表示离心力将增加叶片的广义刚度,即离心刚化现象。
经过整理简化的叶片的广义刚度为
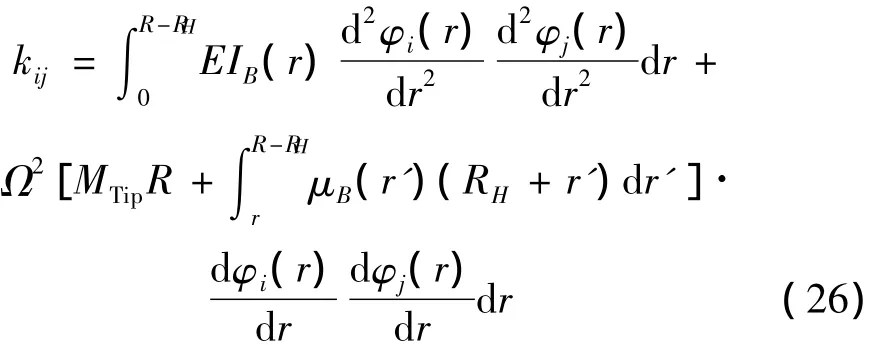
2.3 基于假设模态表示的叶片和塔筒变形
根据叶片和塔筒的模态振型,可以表示叶片和塔筒的柔性变形位移。
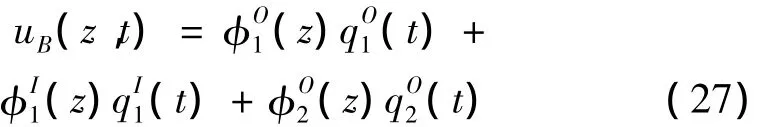
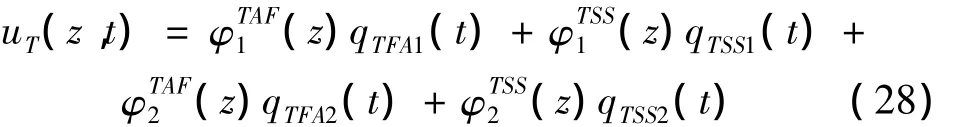
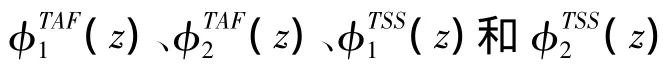
3 修正的BEM空气动力学模型
由于建立BEM理论时所做的假设,经典BEM理论仅适用于轴对称稳态气流中的风轮气动力计算,且没有考虑三维效应的影响,适用范围有限。因此需要对经典BEM理论有重载风轮的CT进行修正[9],以满足实际计算的需要。
当风轮处于高速重载的情况下,叶片上的轴向诱导因子a较大,若a>0.5时,将出现尾流风速UW为负数的情况,即尾流出现了倒流,这显然是不符合实际情况下。实际上,此时的尾流会从周围空气中获得能量,使缓慢通过风轮的气流重新获得能量,风轮上下风向的压力差将产生很大的推力,远远大于动量理论的预测值,因此需要对CT进行修正以反映实际的情况。修正CT值的方法有很多,它们之间的差别在于轴向诱导因子a过渡点和CT曲线的选择。
GH的 Bladed中[9],将a的过渡点的值取为0.353 9,当BEM理论计算得到a大于该值时,用抛物线经验公式:
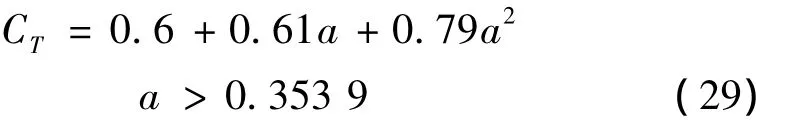
NREL的Aerodyn中,将a的过渡点的值取为0.4,当计算得到的a大于该值时,用抛物线经验公式:
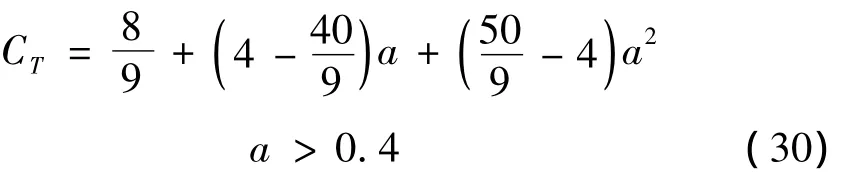
也可以将a的过渡点的值取为0.326 2,用线性经验公式:
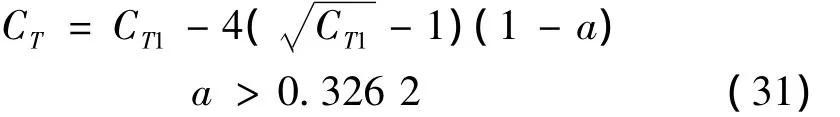
上面的修正关系如图3所示。
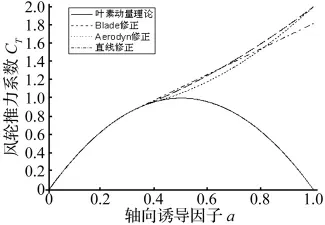
图3 推力系数修正Fig.3 Modified thrust Factor
如图3可见修正后的CT曲线在轴向诱导因子a大于过渡点的值之后,继续上升,表示在重载风轮面存在很大的压力差,相较于经典BEM理论的动量理论[]计算得到的结果,更加符合实际情况。
4 算例与结果
在Fortran环境下编程进行风力机整机的系统动力学数学建模,将采用谱模拟法得到的湍流风风速时间历程加载到修正的BEM空气动力学模型中,进行风力机风轮气动载荷计算。并将到风轮气动载荷输入基于Kane方法建立的风力机全刚体动力学模型中,得到风力机响应曲线。再将所得的风力机响应参数输入到基于假设模态法离散的动力学模型中,获取风力机各部位的变形等信息。同时通过获取风力机叶片与塔架的质量矩阵和刚度矩阵,进行模态分析。在风轮常用转速下,避开风轮1P和3P频率[12],最终实现对风力发电机整机系统的动力学进行随机响应分析。

表1 2MW风力发电机组主要结构参数Tab.1 Paremeters for 2MW wind turbine
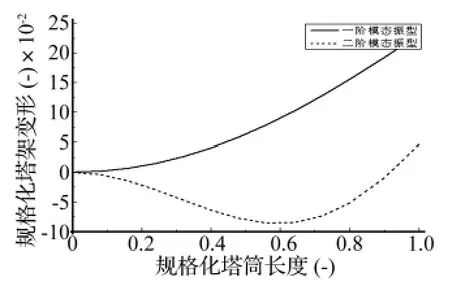
图4 塔筒模态Fig.4 Normalized mode of tower
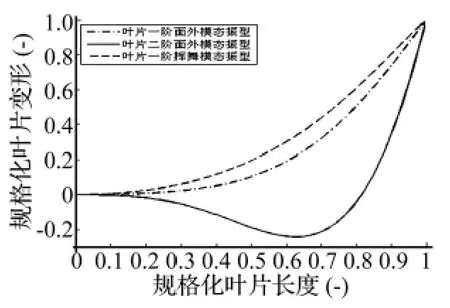
图5 叶片模态归一化Fig.5 Normalized mode of blade
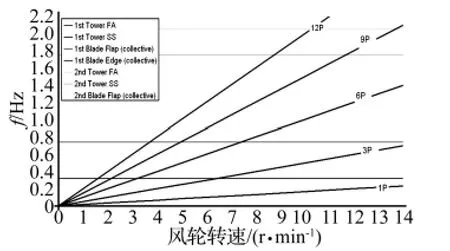
图6 坎贝尔图Fig.6 Campbell Diagram
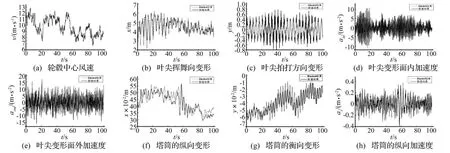
图7 动力学分析结果Fig.7 Results of Dynamic Analysis
本文以企业合作开发的2.5MW风力机进行数值仿真计算,并将数值计算结果与Bladed计算结果进行对比。
图4~图5,分别为塔架和叶片的模态振型。由图6可知,在风轮常用转速7~14 r/min内,塔架与风轮的固有频率均能避开风轮自激频率1P和3P。由图7所示,数值模拟得到动力学结果与Bladed分析结果比较,使用风力机叶片与塔筒的动力学响应结果吻合较好,表明该方法能够较为准确进行风力机动力学建模与分析。
5 结论
本文利用Kane方法建立了风力机系统动力学方程,并根据假设模态法进行离散化,推导出基于柔性梁变形位移场一阶完备的动力学模型。将修正BEM空气动力学模型得到风载荷加载到该风力机结构动力学模型上,进行风力机整机动力学分析。通过某型2.5MW风力机的数值计算,并与同权威计算软件GH Bladed结果进行比较,表明使用Kane方法和假设模态法建立的风力机动力学模型充分考虑了风力发电机组整机结构运动与风速的耦合效应,所建立的整机系统动力学模型更为准确,为开发具备我国自主知识产权的水平轴风力发电机组设计软件奠定了基础。
[1]陈 彦.大型水平轴风力机结构动力响应与稳定性研究[D].北京:清华大学,1999.
[2]窦秀荣.水平轴风力机气动性能及结构动力学特性研究[D].济南:山东工业大学,1995.
[3]Buhl Jr L.A new empirical relationship between thrust coefficient and induction factor for the turbulent windmill state[R].TechnicalReportNREL/TP-500-36834-August,2005.
[4]蔡国平,洪嘉振.旋转运动柔性梁的假设模态方法研究[J].力学学报,2005,37(1):48-56.
[5]蒋丽忠,赵跃宇.作大范围运动柔性结构的耦合动力学[M].北京:科学出版社,2007,5.
[6]盛国刚,李传习,赵 冰.支承运动情况下旋转梁的刚-柔耦合振动分析[J].振动与冲击,2006,25(6):117-120.
[7] Peter D A.Fast floquet theory and trim for multi-blade in rotorcraft[J].J.American Helicopter Society,1994,39(4):82-89.
[8]Jonkman J M.Modeling of the UAE wind turbine for refinement of FAST_AD[R].NREL/TP-500-34755,National Renewable Energy Laboratory,2003.
[9] Patrick J,Moriarty A,Hansen C.Aerodyn theory mannal[M].National Renewable Energy Laboratory,2005.
[10] Bossanyi E A.Bladed G H.Version 3.67 user manual[M].Garrad Hassan &Partners Limited,2005.
[11] Burton T,Sharpe D,Jenkins N.Wind energy handbook[M].England John Wiley & Sons,Ltd,2001.
[12]刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998.
