基于Cox-de Boor递推的任意次NURBS曲线插补算法的研究与仿真

赵玉刚，李 伟，郭 峰，李业富，刘春仙

(1.山东理工大学机械工程学院，山东淄博 255049;2.滕州市产品质量监督检验所，山东 滕州 277500)

基于Cox-de Boor递推的任意次NURBS曲线插补算法的研究与仿真

赵玉刚1，李 伟1，郭 峰2，李业富1，刘春仙1

(1.山东理工大学机械工程学院，山东淄博 255049;2.滕州市产品质量监督检验所，山东 滕州 277500)

论文基于Cox-de Boor递推算法实现了任意次NURBS曲线的插补，利用差分插补方法来预估参数，结合机床实际加工过程中所必需满足的条件，将进给速度，机床最大加速度，最大弓高误差分别约束的参数进行比较，优化出最佳参数值，实现了速度自适应控制。论述了控制顶点、节点矢量、权因子对NURBS的影响，利用二分法线性搜索节点区间，给出了系统生成的NURBS曲线插补的NC代码形式，列出了整个插补算法的流程框图，在C++builder开发环境下完成了对任意次NURBS曲线的插补仿真，验证了算法的可行性。

NURBS插补;任意次;差分预估

0 引言

非均匀有理B样条NURBS(Non-Uniform Rational B-Spines)，它已成为利用计算机处理几何信息时，设计和数据交换的工业标准，如 IGES，STEP和PHIGS等一些国内和国际标准。NURBS为解析曲线曲面(如圆锥截线和二次曲面)和自由型曲线与曲面(如汽车车身和船体外形)的表示提供了一种统一的数学方法。基于NURBS的良好性质，在大多具有自由型面的航空、宇航、模具等制造行业中具有特别重要的意义。

目前绝大多数的数控系统只具备直线、圆弧、抛物线等插补功能，在加工自由型曲面零件时，往往要借助CAM离线编程系统，即把参数表示的自由型曲面细分成大量的微小线段或圆弧后，进行加工。但随着设定误差的减小，细分得到的数据量就会呈几何倍数的速度增加，生成的数据量非常大，使得编程变得复杂，NC代码程序量急剧膨胀。并且在机床加工时也不可避免地会带来了逼近误差，影响工件的加工质量和表面光滑性。如果CNC系统具备NURBS曲线插补功能，就可以避免由离线编程带来的问题，大大提高工件的加工精度和生产效率。

近些年，很多学者对NURBS曲线的插补算法进行深入的研究，取得了很大的发展，但也存在着一些不足，文献［1］在CNC系统中实现了NURBS曲线的实时插补，但是，NURBS曲线导矢的计算比较繁琐;文献［2］以三次NURBS样条曲线为例，提出了一种新的加减速控制方法，实现了进给速度的自适应控制，提高了轮廓加工精度，但是缺少在任意次NURBS曲线插补算法的论述;文献［3－5］，推导出了三次NURBS曲线的插补公式，满足了系统的实时性，利用已经推算好的三次NURBS公式进行插补，这种方法计算速度快，占用内存小，但是牺牲了算法的灵活性，这种算法只能插补三次NURBS曲线，不是三次的曲线，插补出的轨迹曲线就不能满足要求，就需要重新推导公式，灵活性较差。

本文基于Cox-de Boor的递推算法，避免了B样条曲线基函数的迭代求解过程，降低了算法的复杂性，实现了任意次NURBS曲线的插补和速度的自适应控制，并分别介绍了节点矢量、权因子对NURBS曲线的影响，给出本系统生成的NURBS曲线插补的NC代码样例，列出了完整的任意次NURBS曲线插补算法和流程图，并在C++Builder开发环境下实现了任意次NURBS曲线插补算法的仿真，验证了算法的可行性。

1 NURBS曲线的定义和性质

一条p次NURBS曲线可以表示为一分段有理多项式函数:

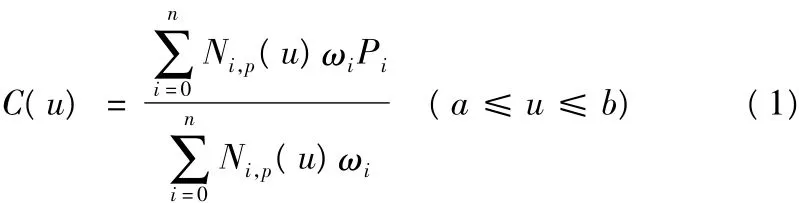
在式(1)中，{Pi}是控制点(它们形成控制多边形)，{ωi}是权因子;每一个控制顶点Pi(0≤i≤n)都附有一个权因子ωi，首末权因子ω0，ωn＞0其余ωi＞0;{Ni，p(u)}是定义在非周期节点矢量U上的p次B样条基函数。

由此可知，一条p次NURBS曲线由3个参数共同决定，分别为:控制顶点，权因子和节点矢量。

由Cox-de Boor递推公式可求得p次Ni，p(u):

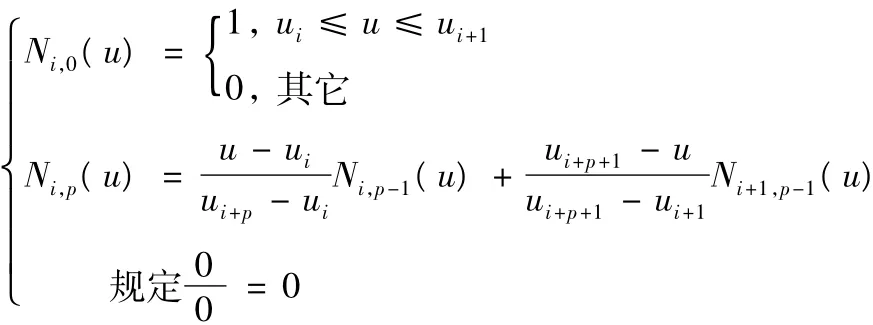
2 节点矢量和权因子

根据Cox-de Boor递推公式可知，节点矢量的确定，直接确定影响着生成的样条基函数，在本文中所研究的NURBS曲线的节点矢量都是非周期、非均匀的。

本文利用弦长法，在已知控制顶点的前提下，自动生成节点矢量。弦长法实现的主要思想:NURBS曲线的首末节点的重复度为p+1，整条NURBS曲线的定义域为［up+1，um－p－1］，将参数化区间规范到［0，1］。

具体做法:NURBS曲线对应的不同控制顶点的累加弦长为:

权因子也可以叫做形状因子，对曲线的局部性修改具有很大的作用，移动控制顶点Pi，或改变权因子ωi，仅影响区间u∈［ui，ui+p+1)上的那部分曲线的形状，这是由样条基函数的递推性质决定的［6］。

设u∈［ui，ui+p+1)，如果 ωi增大(减小)，则点C(u)靠近(远离)Pi，曲线产生被拉向(或推离)Pi的效果。而且对于固定的u，C(u)是沿着一条直线移动。

3 速度的自适应控制

本文在实现速度自适应控制的功能时，借鉴了文献［3］中的高速高精度加工的插补控制，从进给速度、机床最大法向加速度、曲线的最大弓高误差中仲裁出最佳进给步长，从而实现了速度的自适应控制。具体做法如下:

数控系统插补的过程也就是数据密化的过程，即在给定起点和终点的曲线之间插入若干个点，用若干条微小直线段来逼近给定曲线，求得各坐标轴的进给量，即:

在式(2)中，Δli为进给步长，T为系统的插补周期，Fi为给定当前的进给速度。

NURBS的插补算法没有径向误差，只有弓高误差，插补的点都落在NURBS曲线上。弓高误差就是以进给步长代替实际曲线而引起的误差，误差的大小随着进给步长和实际曲线的曲率的增大而增大。

解决方法［3］:引入轮廓误差，在插补过程中，实时监测轮廓误差大小，当误差在加工允许的范围内时，按照进给速度约束的步长进行插补，当误差超出允许的范围，则按照最大允许误差约束步长Δli1进行插补，使得进给步长，能随着实际曲线的曲率变化进行调整，以确保插补曲线的轮廓误差控制在允许的范围内。

计算曲线的曲率比较麻烦，可用曲线段CiCi+1的中点M与弦CiCi+1的中点N之间的距离|MN|来近似表示实际曲线的弓高误差δh，即:

在得到三个约束步长后，经过比较，仲裁求出Δl=min{Δli，Δli1，Δli2}，这样Δl既能满足加工精度，将加速度控制在允许的范围内，也使求得的插补轨迹具有进给速度的自适应能力。

在曲线曲率较大的加工区域，导致曲线的法向加速度过大，超出机床进给系统的承受能力。所以在高速加工时，还要实时监测加速度的变化，当超出机床的最大法向加速度时，按给定的加速度要求调整进给速度。也就是说，以机床的最大法向加速度为约束条件，计算出的约束步长Δli2来代替现有的进给步长 Δli1。

根据给定的允许最大进给加速度amax求得的约束进给步长Δli2为:

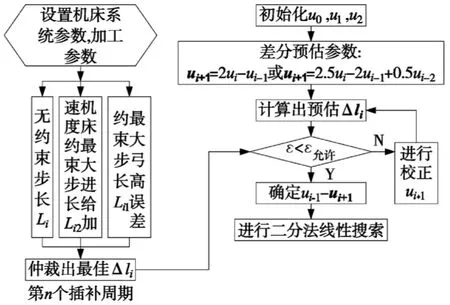
图1 速度自适应算法流程图

4 二分法确定节点区间

在上述仲裁比较得出的最优化的参数ui+1，然后计算ui+1对应的样条基函数，从而确定ui+1对应于NURBS上的点。计算的第一步就是确定ui+1所属的节点区间，本文利用二分法［6］对节点矢量进行线性搜索得到。

二分法搜索的主要思想是:初始赋值low等于最左边的节点矢量，即low=u［p］，high等于最右边的节点矢量，即high=u［n+1］，取中间值mid=(low+high)/2，用需要确定节点区间的ui+1与mid进行比较，如果 ui+1＜ u［mid］，则 high=mid;否则，low=mid;循环进行，直到u［mid］＜ ui+1＜ u［mid+1］。返回的mid，也就是要求的节点区间。

5 NURBS的NC代码格式

一条NURBS曲线由三个参数定义:控制顶点，权因子和节点矢量。将这三个参数作为NC程序指令的一部分，NURBS曲线的NC代码［3］如下表示:

其中:G05为NURBS曲线插补指令，P是要插补曲线的次数，T是割缝的大小(也是刀具半径的大小)，XYZ是控制顶点的坐标，R是权因子，K是节点参数。

CNC系统内部进行实时计算生成NURBS曲线，数控机床按给定的进给速度驱动机床运动，加工出NURBS的曲线形状。图3右为本文设计的数控系统生成的NURBS曲线的NC代码形式。

6 实现的程序框图及仿真图

以一段五次NURBS曲线进行插补为例。8个控制点分别为(－236，－47)，(－223，74)，(－120，103)，( － 47，40)，(－ 12，－ 53)，(101，－ 78)，(202，0)，(236，97)，对应的权因子分别为 W={1，3，3，3，1，3，3，1}。

图2 样条基函数的插补基函数框图

设插补周期 T =0.01s，进给速度 F =1000mm/s，最大允许弓高误差Er=0.0001mm，机床最大法向加速度a=200mm/s2按照上述NURBS曲线的插补流程可以得到如下图的仿真结果。黄色轮廓线为实际轮廓线，红色轮廓线为机床实际加工时经刀补后的的实际轨迹。

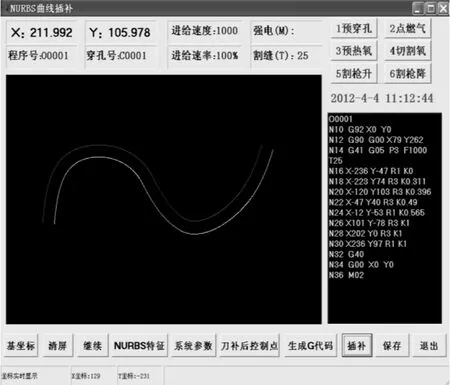
图3 任意次NURBS曲线插补仿真图

7 结束语

本文基于Cox-de Boor的递推算法，实现了任意次NURBS的曲线的插补，列出了完整的任意次NURBS曲线插补算法和流程图，并给出了本系统生成的NURBS曲线插补的NC代码样例，在C++Builder开发环境下实现了任意次NURBS曲线插补算法的仿真，证明了算法的有效性和正确性，具有很大的实用价值。

［1］边玉超，张莉彦，戴莹莹，等.CNC系统中NURBS曲线实时插补算法研究［J］.机械制造与自动化，2003(6):36－39.

［2］赵国勇，徐志祥，赵福令.高速高精度数控加工中NURBS曲线插补的研究［J］.中国机械工程，2006，17(3):291－294.

［3］游友鹏，王珉，朱剑英.NURBS曲线高速高精度加工的插补控制［J］.计算机辅助设计与图形学学报，2001，13(10):944－947.

［4］杜娟，田锡天，张振明，等.基于STEP—NC的CNC系统中插补技术研究［J］.制造业自动化，2005，27(6):24 －27.

［5］徐元凡，刘日亮，张承瑞，等.NURBS曲线插补技术研究［J］.现代制造工程，2009(3):9－12.

［6］Les Piegl，Wayne Tiller.The NURBSBOOK［M］.Second E-dition.Beijing:Tsinghua University Press，2010:46 －89.

［7］William L Luken.Tessellation of trimmed NURBS surface［J］.CAGD，1996(6):163 －177.

［8］Qin H，Terzopoulos D.Triangular NURBSand their dynamic generalizations［J］.Computer Aided Geometric Design.1997(14):325－347.

［9］Welch W，Watkins A.Free-form shape design using triangulated surfaced［A］.New York:Computer Graphics Proceedings，Annual Conference Series，1994，247 － 256.

［10］谢黎明，郑威，靳岚，等.基于NURBS插补算法的嵌入式数控系统的研究与开发［J］.制造技术与机床，2008(7):152－154.

(编辑 李秀敏)

The Random Degree NURBSCurve Interpolation and Simulation Based on Cox-de Boor Algorithm

ZHAO Yu-gang1，LIWei1，GUO Feng2，LIYe-fu1，LIU Chun-xian1
(1.Shandong University of Technology，Shandong Zibo 255049，China;2.Tengzhou City Institute of Product Quality Supervision＆ Inspection，Shandong Tengzhou 277500，China)

This paper realized the random degree NURBS curve interpolation based on the Cox-de boor recursion algorithm;Used differencemethod to estimate the parameters and combined w ith the practical tools necessary to meet the processing conditions，the feed rate，maximum acceleration of themachine，themaximum chord error bound parameters were compared to optim ize the best parameters to achieve a speed adaptive control.This article discussed the control points，knot vector，the weights of the NURBS influence，used the dichotomy nodes to linear search range.It completed random degree NURBS curve interpolation simulation in C++builder development environment，gave the interpolation and interpolation algorithm flow diagram examples to verify the feasibility of the algorithm.

NURBS curve interpolation;random degree;difference estimate

TH161

A

1001－2265(2012)06－0045－04

2011－10－19;

2011－12－20

赵玉刚(1964—)，男，山东淄博人，山东理工大学机械工程学院教授，研究方向为数控与机电一体化技术，(E－mail)zhaoyg9289@sohu.com。