对流-扩散方程数值解的四次B样条方法
2020-11-13齐梓萱
齐梓萱,钱 江
(河海大学理学院,江苏 南京 211100)
样条函数是具有一定光滑性的分段或分片定义的多项式函数,研究多元样条函数一般的方法是光滑余因子协调法[1-2],其他经典方法包括B网方法[3]与B样条方法[4-6]。样条函数方法广泛应用于数值逼近[7]、计算几何[2]、计算机辅助几何设计[6]、有限元、微分方程数值解等领域。
具体而言,文献[8]利用光滑余因子协调法计算出2型三角剖分上的二元三次样条基函数,构造样条拟插值算子[9]及分析拟插值算子导数逼近[10]廖肇源[11]与张胜刚[12]计算了三次样条基函数并将其应用于Poinsson方程的数值求解,取得了好的效果。由于计算的简便性,三次样条函数还被广泛应用于其它微分方程数值解。明祖芬和张大凯[13]给出了三次样条函数及其导数的基本关系,并将其应用于对流扩散问题,给出格式的相容性、收敛性和稳定性条件。吴蓓蓓和徐丽[14]对三次B-样条和三次三角B-样条基函数引入权因子,给出了对流扩散方程的混合三次B-样条配点法。董建强等[15]基于样条插值和Pade逼近公式,构造了一种求解一维对流扩散方程的高精度差分格式。CHANG等[16]提出一种基于样条的运动方法,并用四次样条曲线表示物体的外部轮廓,将其应用于基于图像的IBVS的轮廓跟踪任务中。KERSEY[17]将样条混合差值与样条的光滑性推广到实际问题。文献[18]提出一种基于局部算法的B样条函数拟合任意形式曲线的新方法,并通过实验数据验证其可用于自动逆向工程领域。
然而考虑到更高次样条函数计算的复杂性与逼近具有更高的精度,高次样条函数在微分方程数值解中的应用值得进一步研究。本文将利用光滑余因子协调法求解一元四次B样条基函数,并将其应用于求解一类对流-扩散方程。
1 均匀四次B样条基函数的计算
定理1[2]. 设一个一元n次样条s(x)∈Sn(x0,x1,···,xN)的互异节点为{x0,x1,···,xN},且具有局部支集(x0,xN),则此样条函数可表示为

并且相邻两区间的样条函数满足si(x)-si-1(x)=ci(x-xi)n,i=0,1,···,N且满足协调方程。
利用定理1,可计算出任意次非均匀B样条基函数,拟将样条逼近方法应用于微分方程数值解,本文计算出均匀节点上的四次B样条基函数,且计算有限区间端点处的非均匀四次B样条基函数。
节点为{xi,xi+1,xi+2,xi+3,xi+4,xi+5}均匀步长为h的四次B样条函数。

令ci+5=λ,则ci+4=-5λ,ci+3=10λ,ci+2=-10λ,ci+1=5λ,ci=-λ,得到四次B样条函数为

再利用B样条基函数的单位分解性可得

定理2.步长为h的均匀节点{xi,xi+1,xi+2,xi+3,xi+4,xi+5}四次B样条函数为且在子区间Ii:=[xi,xi+1]中存在唯一一组四次B样条基函数
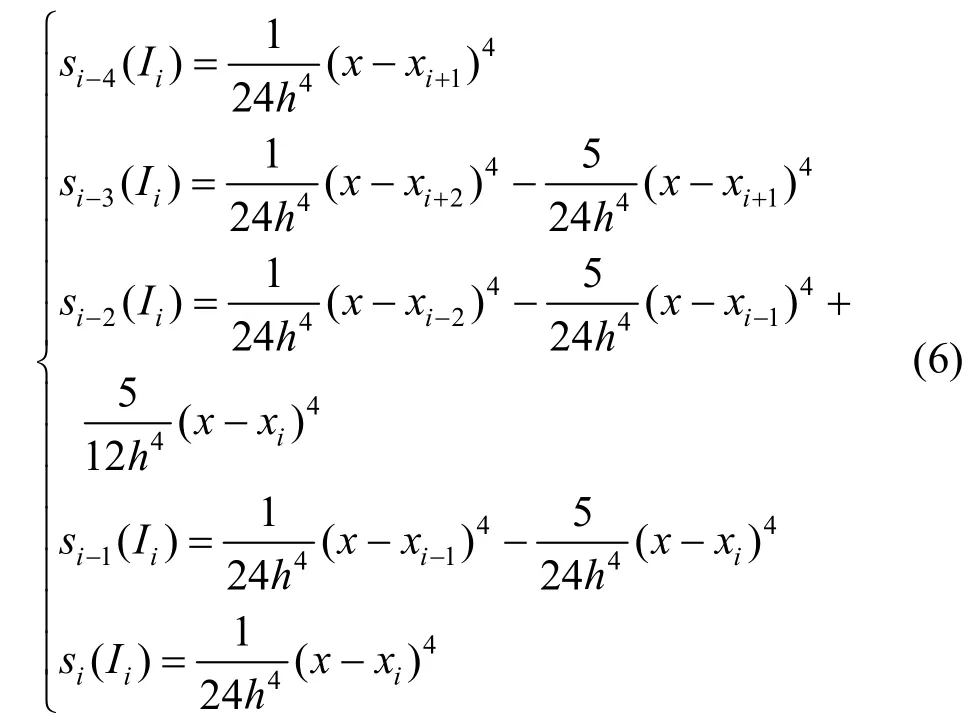

如图1所示,所得的均匀四次B样条基函数具有非负性、单位分解性。

图1 四次B样条基函数Fig. 1 Univariate quartic b-spline bases
2 区间端点带重节点的样条基函数
本文考虑在有界闭区间[x0,xn]内均匀步长为h,将得到在x0,xn处具有重节点的四次B样条的具体表示,从而得到每个支集上的四次样条函数。
情形1.考虑x-1=x0<x1<x2<x3<x4,设在节点x-1=x0,x1,x2,x3,x4处的光滑余因子分别为。可得协调方程为,即

因此节点为x-1=x0<x1<x2<x3<x4时的四次B样条函数为

情形2.x-2=x-1=x0<x1<x2<x3,设节点x-2=x-1=x0,x1,x2,x3处的光滑余因子分别为。协调方程为

同理可得在节点为x-2=x-1=x0<x1<x2<x3时的四次B样条函数为

情形3.x-3=x-2=x-1=x0<x1<x2,记节点x-3=x-2=x-1=x0,x1,x2处的光滑余因子分别为。协调方程为

同理可得节点为x-3=x-2=x-1=x0<x1<x2时的四次B样条函数为
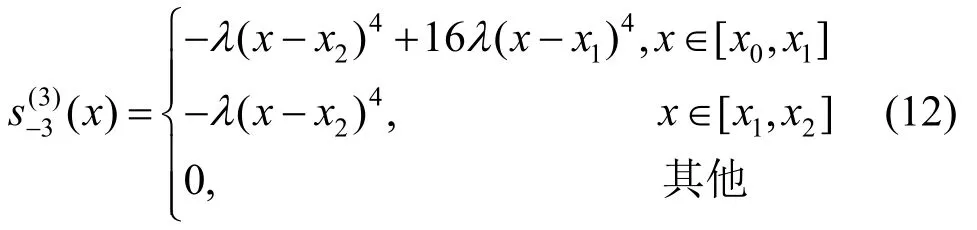
情形4.x-4=x-3=x-2=x-1=x0<x1,设 节 点x-4=x-3=x-2=x-1=x0,x1的光滑余因子为。协调方程为

同理可得在节点为x-4=x-3=x-2=x-1=x0<x1时的四次B样条函数为
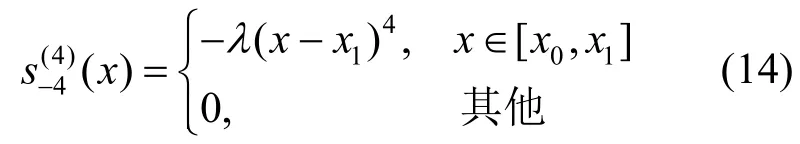
定理3.节点为x-4=x-3=x-2=x-1=x0<x1<x2<x3<x4<x5且xi+1-xi=h i=0,1,···,5时,在每个子区间内存在唯一一组四次B样条基函数为


证明:在单区间I0=[x0,x1]内存在的B样条函数有
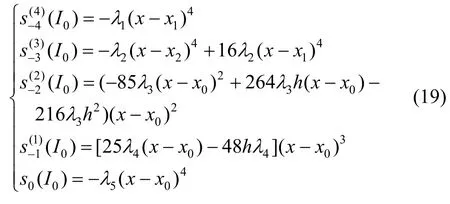
由B样条基函数的单位分解性知
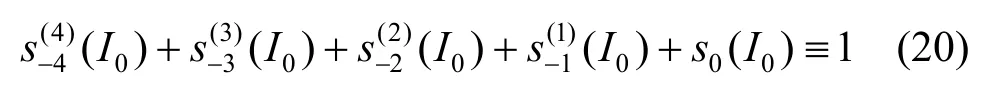
由此得到式(15)。同理可证得式(16),(17),(18)。
证毕
类似于对左端点x0处带重节点的四次B样条的分析,同样可以得到右端点xn处带重节点的四次B样条的结论。
定 理4.设xn-5<xn-4<xn-3<xn-2<xn-1<xn=xn+1=xn+2=xn+3=xn+4且xi+1-xi=h,i=n-5,n-4,···,n-1,则在每个子区间内存在唯一一组的四次B样条基函数


证明:在单区间In-1=[xn-1,xn]中,存在的B样条函数有

由B样条基函数的单位分解性知
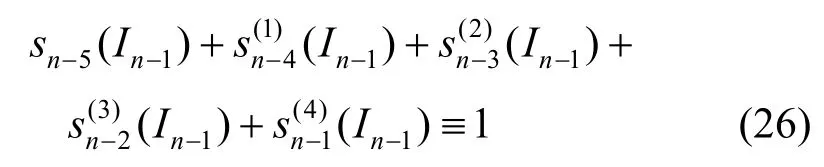
同理可证得式(22),(23),(24)。
证毕
3 对流-扩散方程的样条逼近离散格式
考虑一维对流-扩散方程

其中,θ是关于空间x与时间t的二元函数,其为在时刻T点x处的体积浓度;u为对流速度;Dx为扩散系数,函数f(x),g0(x),g1(x),g2(x)是充分光滑的。
表1为函数si(x)及其导数在各节点处的值。

表1 si(x)及其导数在各节点处的值Table 1 The value of si(x) and its derivative at each node
记点(xi,tk)处的逼近解为在区间[xi,xi+1]上为。

点(xi,tk)处时间变量采用一阶向前差分,引入参数δ(0≤δ≤1),式(27)可离散化为

将式(30)带入式(31)中,生成具有n+4个未知量的n+1个方程。为了使方程组具有唯一解,还需要另外添加3个方程。由边界条件可得

n+4个方程组的矩阵表示为






求出C0则第k+1时间层的逼近解便可由式(33)计算得到。
另外,若采用向前差分法,右边值采用向后差分离散方程,则得到的矩阵表示为



由于所采用的四次样条基函数具有非负性与单位分解性,因此求解过程是稳定的,且精度高于基于三次样条得到的求解结果。限于篇幅,后续将进一步研究基于四次B样条的样条拟插值算子,并将其应用于求解偏微分方程,从理论上分析四次样条求解微分方程的稳定性与收敛性。
4 数值算例
考虑对流-扩散方程

其准确解为

方法1.样条逼近方法。根据式(31)并取参数δ=0.5,得到
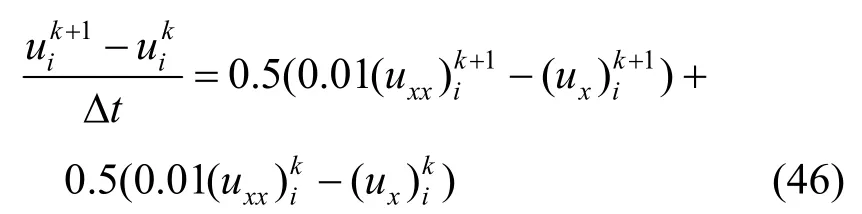
取时间步长Δt=0.04,空间步长h=0.02,得Ck+1满足式(33),其中,。C0满足式(36),可求得C0=(1.0304,1.0100,0.9900,0.9704,0.9512,0.9323,0.9139,···,0.4025,0.3945,0.3867,0.3791,0.3715,0.3642,0.3570)T。由此可通过式(33)解得相应的Ck+1。
方法2.有限差分法。用差分方法离散方程,同样取δ=0.5,离散化得

取Δt=0.04,h=0.02,可得式(34),其中,,,。
表2取t=0.2,对x取不同值与文献[13]中的三次样条解做比较。
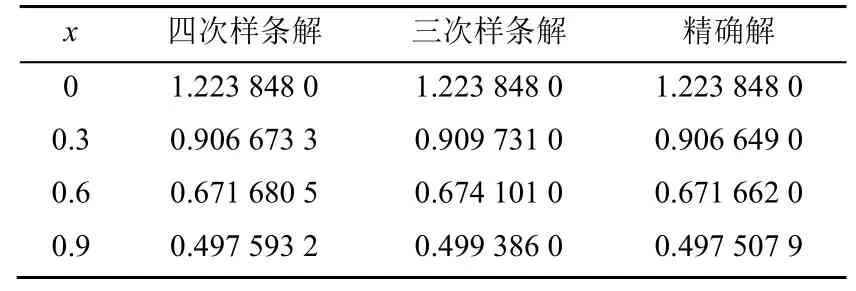
表2 四次样条解与三次样条解对比Table 2 The quartic spline solution is compared with the cubic spline solution
表3为表2的2种方法所求解与精确解的数值误差对比。

表3 数值误差对比Table 3 Numerical error comparison
表4取t=0.04,在[0.9,1.0]区间内与差分方法的解进行比较。
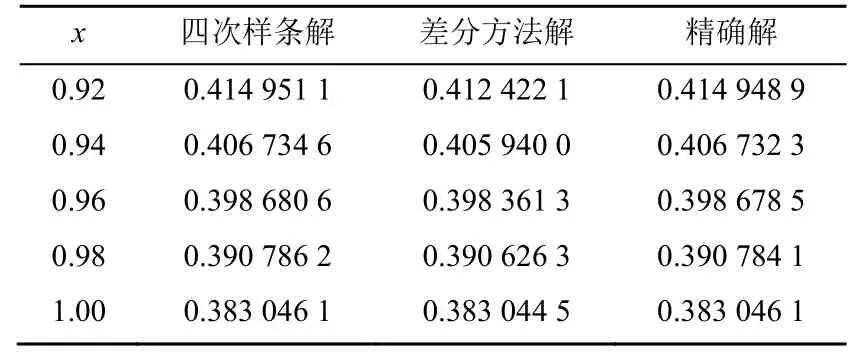
表4 四次样条解与差分方法解对比Table 4 The quartic spline solution is compared with the difference method solution
表5为2种方法所求解与精确解的数值误差对比。

表5 数值误差对比Table 5 Numerical error comparison
对于式(42)的离散,方法1和方法2均对时间变量在(xi,tk)处取一阶向前差分,而对空间变量的离散,方法1引入参数δ并在(xi,tk),(xi,tk+1)处取样条函数的一阶、二阶导数形式;方法2需要考虑2种差分方式,同样引入参数δ对方程进行一阶及二阶向前差分,对于右端点的处理采用一阶及二阶向后差分。进一步,本文算例中通过对2种方法进行数值比较可知,样条方法的逼近效果更好,且Matlab计算表明,采用样条逼近方法得到解的时间为5.939 365 s,而有限差分法运行的时间为10.668 284 s。因此,选择样条逼近方法更简便实用。并且通过对于t=0.2时与三次样条逼近解的对比可知,四次样条的逼近比三次样条逼近效果好。
