HHT和Morlet小波变换在齿轮故障信息提取中的对比研究*

成钰龙，程 刚，沈利华，邱锦波，张 帅

(1.中国矿业大学 机电工程学院，徐州 221116;2.天地科技股份有限公司上海分公司，上海200030)

HHT和Morlet小波变换在齿轮故障信息提取中的对比研究*

成钰龙1，程 刚1，沈利华2，邱锦波2，张 帅1

(1.中国矿业大学 机电工程学院，徐州 221116;2.天地科技股份有限公司上海分公司，上海200030)

文章描述了基于振动信号的Morlet小波变换和HHT(Hilbert-Huang变换)齿轮故障信息提取方法，并分别用来对四类齿轮进行故障信息提取，得到各状态齿轮振动信号的Morlet小波谱和Hilbert谱。实验研究表明：Morlet小波变换和HHT都可用于齿轮故障信息提取，但Hilbert谱分析比Morlet小波谱分析在时间和频率域都有较高的分辨率，且HHT比Morlet小波变换有更高的计算效率，更适用于故障信号微弱、振动信号数据量大的齿轮故障信息提取。

振动信号;Hilbert-Huang变换;Hilbert谱;Morlet小波谱;故障信息提取

0 引言

齿轮是机械传动系统中的重要部件，其故障发生率较高，任何齿轮故障都会导致机器工作效率的降低，甚至引发严重的事故。齿轮故障在运行中主要表现为裂纹、断齿、齿面磨损和点蚀等，而这些故障在正常工作条件下一般不易发觉。因此，开展齿轮故障信息提取，及早实现其故障诊断尤为重要。

通过振动信号的检测来进行齿轮故障分析是最常用的齿轮故障诊断方法［1］，传统的测试数据处理方法如Fourier变换可以将信号转换到频率域进行分析，但齿轮在工作过程中受到刚度非线性、摩擦力、非平稳载荷等因素的影响，其振动信号往往表现出非平稳特征，而Fourier变换是在全局概念及平稳性假设的基础上开展的［2］，因此在非平稳信号处理方面，Fourier变换已无能为力，取而代之的是小波变换等非平稳信号处理方法［3］。小波变换是至今为止一种很好的时频分析方法，小波分析具有多尺度特性和“数学显微”特性，能较好地实现对信号全貌及其局部特性的双重分析，为机械故障诊断中的非平稳信号分析、弱信号提取、信号滤波等提供一条有效的途径。但其自身也存在一些不可避免的缺陷如边缘失真及能量泄露等［4］。HHT作为最近流行的时频分析方法，能基于信号的局部特征时间尺度，把复杂的信号函数分解为有限的IMF之和，同时HHT不会造成信号能量的扩散和泄露［5］，因此这种自适应的信号处理方法非常适用于非线性和非平稳过程，具有很高的信噪比。但HHT中经验模式分解存在频谱混叠现象［6］，在分析时频率谱的变化容易造成识别困难。本文基于振动信号分别用Morlet小波变换和EMD(经验模型分解)算法对四类齿轮进行故障信息提取，并通过对两种方法的分析结果进行对比研究，证明HHT更适用于齿轮故障信息提取。

1 基于Morlet小波变换的齿轮故障信息提取

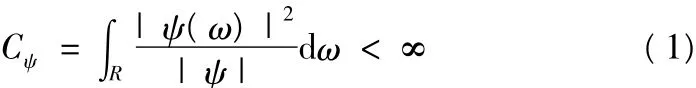
小波是一种特殊的长度有限且均值为0的波形［7］，假设ψ(t)为一平方可积函数，其傅里叶变换满足条件:则称ψ(t)为一个基本小波。小波变换即将信号分解成一系列由一个基本小波函数经过平移与尺度伸缩所得小波函数的叠加。其表达式为:

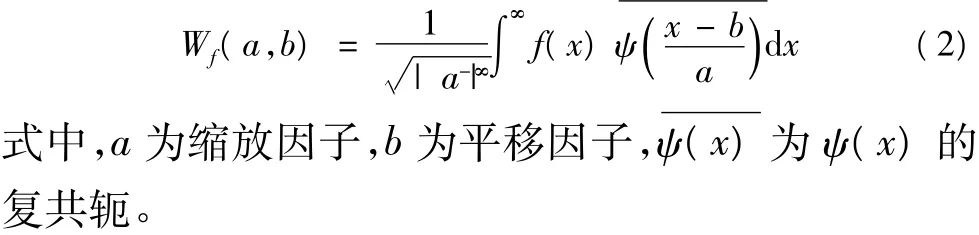
常用小波有Haar小波、Daubechies(dbN)小波、Morlet小波等，其中Morlet小波采用时频窗面积最小的高斯函数，时频域局部化性能好，并且有较好的对称性［8］，故选用Morlet小波作为母小波对所采集原始数据进行处理，Morlet小波表达式为:

所采集的各状态齿轮原始振动信号波形如图1所示，图中竖轴表示振动幅值，单位为V，从图中不能看出故障信号的存在。利用Morlet小波对其进行处理，计算机经过三分钟的计算，得到Morlet小波谱分析图如图2所示，图中左竖轴表示信号频率，单位为Hz，右竖轴用不同的颜色表示振动幅值，图3也是如此。

图1 不同齿轮状态的振动信号

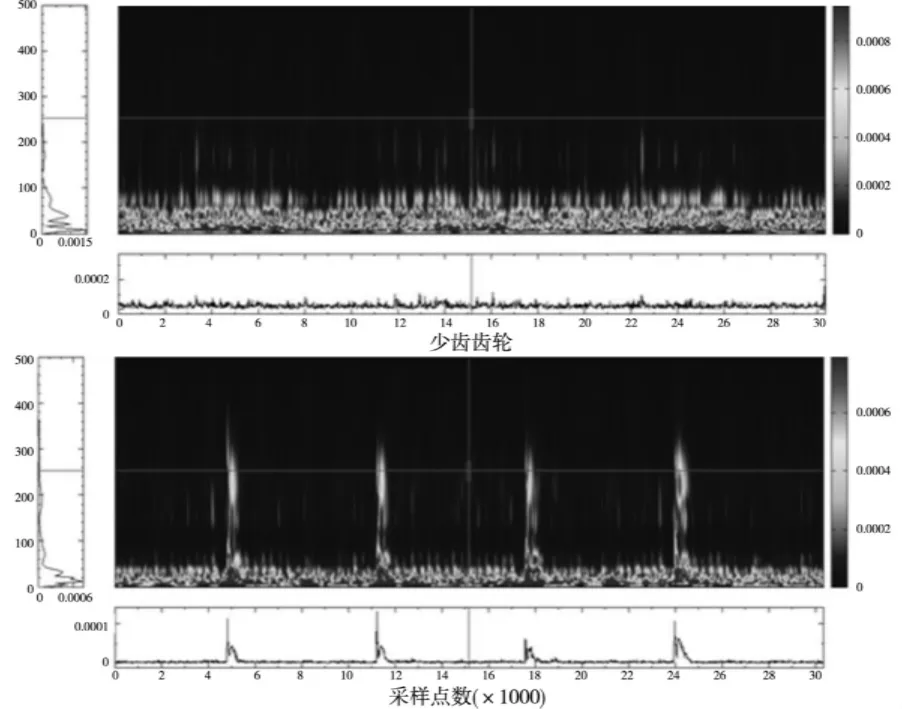
图2 Morlet小波谱分析图

从Morlet小波谱分析图中可以看出，四种齿轮振动信号的主频率都在20Hz附近，这与实验所设定的齿轮啮合频率一致。正常齿轮振动信号的高频成分较少，且其振动幅值较小，并呈现出一定的周期性，说明其能量大都集中在低频部分，齿轮在运转过程中存在一定的周期性干扰信号。磨损齿轮的高频振动信号较正常齿轮明显增多，说明磨损加剧了齿轮的振动，对齿轮的平稳运行有一定的影响。断齿齿轮的高频振动信号较磨损齿轮又有所增加，说明齿轮断齿对齿轮运转影响更大。少齿齿轮的Morlet小波谱分析图中出现明显的周期性高频信号，且其振动幅值较大，表明少齿对齿轮运行带来明显的周期性影响，危害性最大。实验结果与四种齿轮实际状态相吻合，说明Morlet小波变换可以有效提取齿轮故障信息，并用于齿轮故障诊断。

2 基于HHT的齿轮故障信息提取及其与Morlet小波变换的对比

Hilbert-Huang变换包括EMD和相应的Hilbert变换。EMD通过多次移动过程，消除信号中的骑行波(小尺度波“骑行”在大尺度波上，叫骑行波)，并对高低不平的信号进行平滑化［9］。由Hilbert变换所得Hilbert谱能精确地描述信号的幅值随频率和时间变化而变化的规律。

忽略原信号的余项，对信号进行EMD之后所得各IMF做 Hilbert变换，用 ci(t)表示各 IMF，其Hilbert变换表达式如下:

这就称作Hilbert谱。

原始振动信号获取之后，经过EMD分解，得到IMF分量，根据式(6)对各IMF分量作Hilbert变换，计算机用时不到一分钟，便得到对应的Hilbert谱H(ω，t)，图3为四种状态齿轮振动信号的Hilbert谱分析结果。从图中可以明显看出，四种齿轮振动响应信号的主频率都集中在齿轮啮合频率20Hz附近，少齿齿轮的Hilbert谱高频部分有明显的周期，其故障频率在200Hz以上。其余三种状态齿轮的Hilbert谱无明显故障周期特性，正常齿轮高频部分的振动信号几乎没有，磨损齿轮的中高频振动信号增多，断齿齿轮的中高频振动信号明显增多。由此可以实现齿轮故障信息的提取并清楚区分齿轮的四种状态。

对比图2与图3，可以发现 Hilbert谱图要比Morlet小波谱图更清晰，说明Hilbert谱分析在时域和频域都比Morlet小波谱分析有较高的分辨率。另外，使用Morlet小波变换进行齿轮故障信号提取需要三分钟，而使用Hilbert谱分析只需不到一分钟便可准确提取齿轮故障信息。对一种时频信号分析方法来说，高分辨率和高的运作速度都是很重要的因素，所以Hilbert谱分析比Morlet小波谱分析更适用于齿轮故障诊断信号的提取。

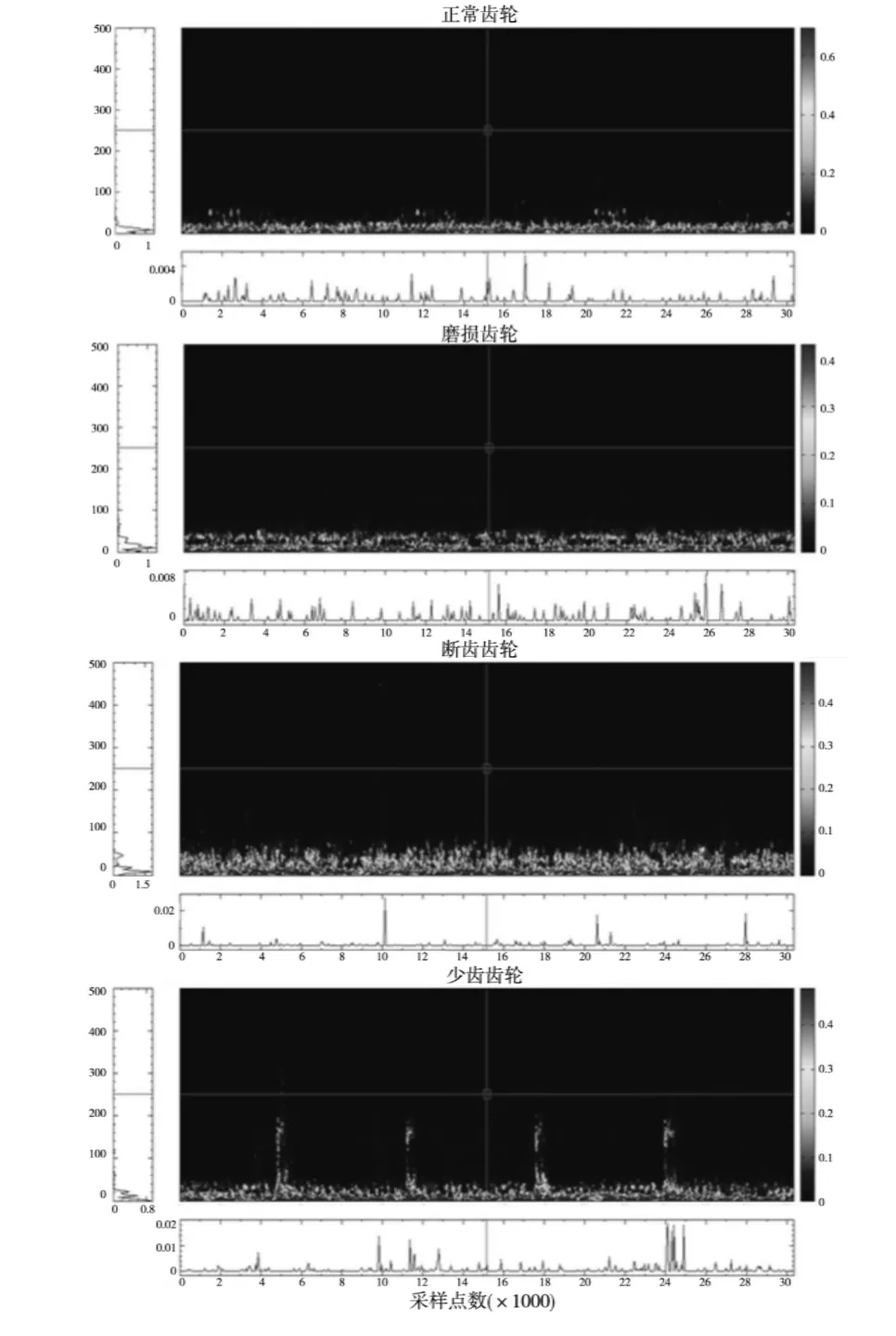
图3 不同状态齿轮振动信号的Hilbert谱分析

3 结束语

本文分别使用HHT和Morlet小波变换对四种齿轮的振动信号进行了分析，分析结果表明HHT和Morlet小波变换都可以对齿轮故障信息进行有效提取，但是Hilbert谱在时频域的分辨率都比Morlet小波谱的分辨率高，且Hilbert谱分析的计算速度比Morlet小波谱分析的计算速度要快很多。所以HHT比Morlet小波变换更适用于微弱振动信号的检测，而且更适用于大数据量振动信号的分析。

［1］王江萍，孙文莉.基于小波包能量谱齿轮振动信号的分析与故障诊断［J］.机械传动，2011，35(1):55－58.

［2］V.K.Rai，A.R.Mohanty.Bearing fault diagnosis using FFT of intrinsicmode functions in Hilbert－Huang transform［J］.Mechanical Systems and Signal Processing，2007，21(2):2607－2615.

［3］黄天戍，谭风华，任清珍.基于小波算法的故障信号特征抽取［J］.组合机床与自动化加工技术，2005(9):77－82.

［4］鞠萍华，秦树人，秦毅，等.多分辨EMD方法与频域平均在齿轮早期故障诊断中的研究［J］.振动与冲击，2009，28(5):97－101.

［5］Rafiee J，Rafiee M A，Tse P W.Application of mother wavelet functions for automatic gear and bearing faultdiagnosis［J］.Expert Systems with Applications，2010，37(6):4568－4579.

［6］Y.H.Liu.Fault diagnosis based on SWPT and Hilbert transform［J］.Procedia Engineering，2011，15:3881 －3885.

［7］杨超，王志伟.基于小波分析和模糊神经网络的齿轮故障诊断研究［J］.噪声与振动控制，2010，20(4):64－67.

［8］陶顺兴，周晓军，张志刚.基于复Morlet小波和系数相关的齿轮故障特征提取［J］.机械科学与技术，2010，29(5):642－650.

［9］徐龙云，芮执元，冯瑞成.基于Hilbert－Huang变换的齿轮故障诊断研究［J］.机床与液压，2010，38(3):133－136.

(编辑 赵蓉)

A Comparison Study of HHT and Morlet W avelet Transform in App lication to Fault Information Extraction for Gears

Morletwavelet transform and HHT(Hilbert-Huang Transform)based on vibration signalwere described in this paper as gear fault information extraction method，then they were used to extract four kinds of gear fault information，and Morletwavelet spectrum and Hilbert spectrum of gear vibration signal were obtained.Studies showed that both Morlet wavelet transform and HHT can be used for gear fault information extraction，but Hilbert spectrum analysis had higher resolution than Morletwavelet spectrum analysis in both time and frequency domain，and HHT had higher computational efficiency than Morletwavelet transform，so HHT wasmore suitable for gear fault information extraction w ith weak vibration signal and large quantity of vibration data.

vibration signal;Hilbert-Huang transform;hilbert spectrum;morletwavelet spectrum;fault information extraction

TP391.4

A

1001－2265(2012)06－0035－03

2012－03－18;

2012－03－31

863基金项目(2012AA06A406)

成钰龙(1988—)，男，山西吕梁人，中国矿业大学硕士研究生，研究方向为机械故障诊断，(E－mail)chengyulong@cumt.edu.cn。CHENG Yu-long1，CHENG Gang1，SHEN Li-hua2，QIU Jin-bo2，ZHANG Shuai

(1.College of Mechanical and Electrical Engineering，China University of Mining ＆ Technology，Xuzhou 221116，China;2.Shanghai Branch of Tiandi Science ＆ Technology Co，Ltd.，Shanghai200030，China)