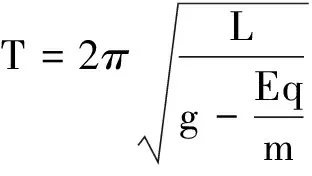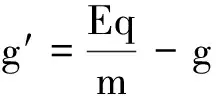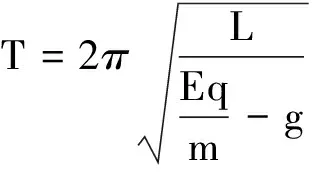“等效重力”在高中物理解题中的应用
2012-01-23温春奎
温春奎
(梅河口市第五中学 吉林 通化 135000)
“等效重力”是等效思维在解题过程中的具体应用,是培养学生思维能力的有效途径.用这种方法求解带电小球在匀强电场中的运动问题会收获意想不到的效果,即把生疏的复合场问题转化为熟知的重力场问题,使解题思路更加畅通.
1 求解匀强电场中的抛体运动问题
【例1】如图1所示,在场强为E,水平向右的匀强电场中,以初速度v0竖直向上抛出一个质量为m,电荷量为+q的带电小球,求:(1)小球在运动过程中的最小速度;(2)从抛出到速度最小经历的时间(空气阻力不计).
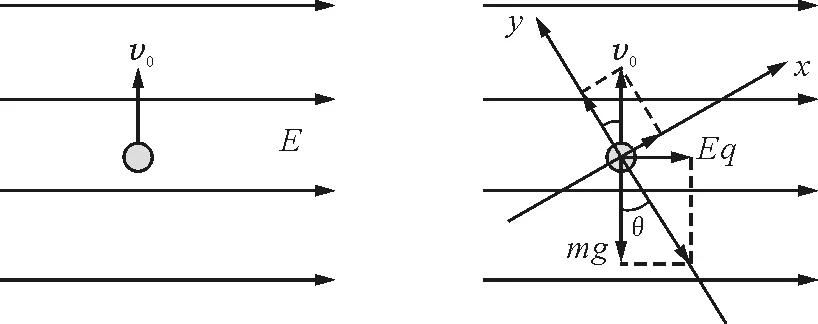
图1 图2
解析:小球在运动过程中受重力mg和电场力Eq(恒力)的作用,把这两个力的合力作为“等效重力” ,该问题就转化为重力场中的斜上抛运动,可用运动分解的方法求解.
v=vx=v0sinθ
由图2可得
所以,最小速度为
(2)当vy=0时,由vy=v0cosθ-at得
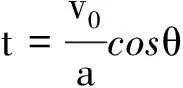
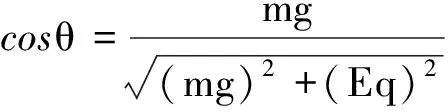
所以,从抛出到速度最小经历的时间为
该题的常规解法是建立正常的坐标系,将小球的运动分解为水平向右的匀加速直线运动和竖直上抛运动,当合速度与合力垂直时速度最小(这个条件学生不易想到).这样解比上述解法繁琐很多,这里不再赘述.
2 求解匀强电场中圆周运动的临界问题
【例2】如图3所示,在竖直平面内有E=1.0×104N/C的水平向右的匀强电场. 一个质量为m= 0.04 kg,电荷量为q=3×10-5C的小球,用长为R=0.4 m的细绳拴住,悬挂在电场中的O点,当小球静止时处于图中的A点.为使小球在竖直面内做完整的圆周运动,在A点至少给小球多大的初速度?
(取g=10 m/s2)

图3
解析:该题是重力场中圆周运动临界问题的进一步演变.如果把重力和电场力的合力看成一个力,即“等效重力”,小球就只受“等效重力”和绳的拉力.不同的是临界点的位置发生变化,这是问题的关键.
设“等效重力”的大小为F,则
方向与竖直方向夹角为θ,且
得
θ=37°
A点为“等效最低点”,B点为“等效最高点”,能到达B点就能在竖直面内做完整的圆周运动.到达B点时有
TB=0时,vB最小,且
从A到B由动能定理得
解得
vA=5 m/s
即为最小速度.
如果本题不用“等效重力”的方法,“等效最高点”将无法体现,误把C点当做“最高点”,这是学生易犯的错误.
拓展:当vA=5 m/s时,求小球运动到C,D和A点时绳对小球的拉力分别是多大.
(1)从B到C,根据动能定理得
解得

在C点,根据牛顿第二定律得
(电场力对向心力没有贡献,不用“等效重力”简单)
解得
TC=0.3 N
(2)从B到D,根据动能定理得
解得
在D点,根据牛顿第二定律得
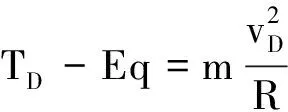
(重力对向心力没有贡献,不用“等效重力”简单)
解得
TD=2.4 N
(3)运动到A点时,根据牛顿第二定律得
(重力和电场力对向心力都有贡献,用“等效重力”简单)
解得
TA=3.0 N
变式训练:如图4所示,把小球穿在半径为R=0.4 m的光滑圆环上,并把圆环固定在竖直面内,其他条件不变,求:(1)在A点至少给小球多大的初速度才能使小球在竖直面内做完整的圆周运动;(2)把小球从最高点C由静止释放,小球在运动过程中的最大速度;(3)把小球从A点拉开一段很小的距离并由静止释放,求小球运动到A点所用时间.
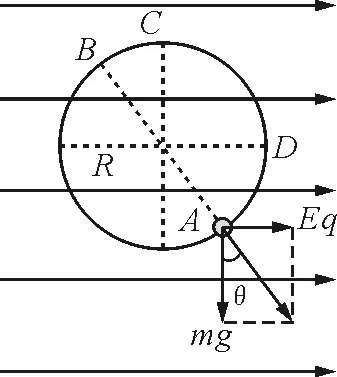
图4
解析:(1)“等效最高点”为B点,“等效最低点”为A点,但圆环既可以“拉”球也可以“支”球,因此,小球到B点时的最小速度可以为零,这是与原题不同之处.
从A到B,根据动能定理得
解得
(2)因为A点为“等效最低点”所以,小球运动到A点时速度最大.从C到A,根据动能定理得
解得
(3)小球释放后,在A点两侧往复运动,由于拉开的距离很小(远小于R),小球的运动可等效为单摆.“等效摆长”为L=R,“等效重力加速度”为g′,可由“等效重力”求得

从释放到A点所用时间为
3 求解匀强电场中单摆的周期
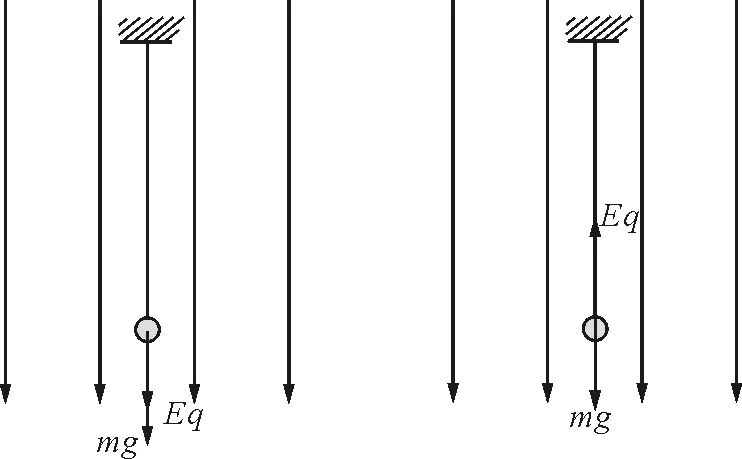
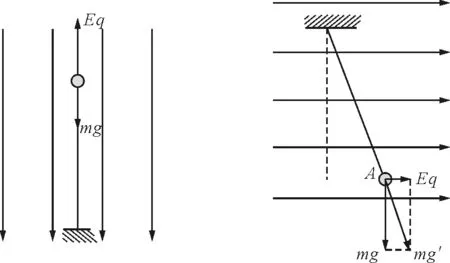
(1)摆球带+q(-q) ,匀强电场竖直向下(上),场强大小为E, 则“等效重力”为
mg′=mg+Eq
方向竖直向下,如图5所示.
“等效重力加速度”大小为
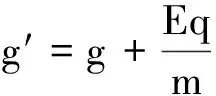
所以
平衡位置不变,周期变小.
(2)摆球带+q(-q),匀强电场竖直向上(下),Eq mg′=mg-Eq “等效重力加速度”为 所以 平衡位置不变,周期变大,如图6所示. 图5 图6 Eq>mg时 ,“等效重力”为 mg′=Eq-mg(竖直向上) 等效重力加速度为 所以 平衡位置在悬点正上方(倒挂),如图7所示. 图7 图8 (3)如图8所示,匀强电场为水平方向时,“等效重力”为 “等效重力加速度”为 所以 平衡位置在“等效最低点”A. 上述实例表明,带电小球在匀强电场中运动时受到的电场力(恒力)和重力的合力可等效为一个力即等效重力,等效重力与质量的比值即等效重力加速度.等效重力的方向决定等效重力加速度的方向及等效最高点和等效最低点的位置.这对解题非常重要.