一道 “复合场”试题的三种解法

张会丽

(登封市第一高级中学 河南 郑州 452470 )

带电体在复合场中的运动是高中物理电学部分的重点，也是难点，当然也是高考的重要考点，在高中物理新课程中也必然占有重要的份量.学生要想灵活应用这一部分的知识，就必须对带电粒子单独在重力场、电场和磁场中运动的规律准确地掌握,对力学的牛顿运动定律、动能定理、能量守恒定律、动量定理等规律清楚地认识.下面对一道关于复合场的高考题中三种解法进行比较，旨在让读者对带电粒子在复合场中的运动认识得更深刻，理解得更透彻.

【例】在场强为B的水平匀强磁场中，一质量为m，带正电q的小球,在O点静止释放，小球的运动曲线如图1所示．已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g．求：

图1

(1)小球运动到任意位置P(x，y)的速率v;

(2)小球在运动过程中第一次下降的最大距离ym;

解法1:常规解法

(1)由于小球在下落过程中，洛伦兹力总与速度方向垂直，不做功，只有重力做功,所以

(2)小球从O点运动到最低点的过程中只有重力做功，所以

图2

小球的受力情况如图2所示.由牛顿第二定律

由以上两式得

(3)小球受电场力和重力的合力向上，将向上运动，同时受洛伦兹力，运动类型和只受重力和洛伦兹力时相同，所以在最高点时速度最大，根据题意，可大胆地猜想得出，在最高点时曲率半径仍为该点到x轴距离的2倍.所以

再由动能定理得

可得

解法2:从运动的合成与分解的角度进行分析

带电粒子受到恒定的力F(忽略重力)在匀强磁场B中，从坐标原点O无初速度的开始运动，可从运动分解的角度把初速度分解为一个沿x轴正方向的速度v和一个沿x轴负方向的速度v′=v，且qvB=F，这样小球的运动可看作是初速度为v′的匀速圆周运动，向心力为qv′B,和圆心沿x轴正方向的速度为v的匀速直线运动的合运动.释放点O为小球运动的最高处，即圆周运动的最高处，如图1所示，当小球运动到最低点时，小球运动的速度为2v，小球运动的合外力为

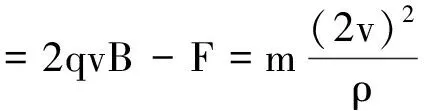
式中的ρ为运动轨迹最低处的曲率半径.而在圆心参考系中，有

式中R为圆周运动的圆半径，由以上两式可得ρ=4R，即得到在平行于y轴方向向下恒力F的作用下,小球从静止开始在匀强磁场中做曲线运动时，当它运动到最低处运动轨迹的曲率半径等于该点到x轴的2倍.可见，这种结论具有普适性.

解法3:用动量定理分析[主要分析第(2)问]

题上已知条件是小球运动轨迹曲线在最低点时的曲率半径为该点到x轴距离的2倍，事实上这个条件是可以证明出来的，是普适的.

证明如下:

小球在重力和洛伦兹力的作用下做曲线运动，重力为恒力，洛伦兹力总与速度垂直，小球做曲线运动.

运动中任意位置的受力情况如图2所示.在图3中，v为这一时刻的瞬时速度，vx,vy为这一时刻的水平和竖直分速度.

qvyB,qvxB为这一时刻洛伦兹力的水平分量与竖直分量.

从这一时刻起，经极短一段时间Δt，列水平方向的动量定理式子

qvyBΔt=mΔv

图3

式中Δv为时间Δt内水平方向的速度增量.对于小球，把它从O点到最低点的过程中，时间分成无数个Δt，对于每一个Δt都可以列出一个水平方向的动量定理方程，再把这些方程求和，即

可得

qBym=mv1

(1)

由动能定理

(2)

由式(1)、(2)可得

再由最低点牛顿第二定律得

(3)

联立式(1)、(2)、(3)可得R=2ym

可见，当小球运动到最低点时，曲率半径一定等于该点到x轴距离的2倍.

第(3)问和第(2)问方法相同，仍利用水平方向动量定理.

这道题是一个复杂的复合场的题目，笔者从3个方面用3种方法分析了这道题，当然大家可能还有其他的解法，通过分析可以对这种题型有一个更加清晰的理解.教师在教学中也应当对重要的题型多加钻研，鼓励学生学会发散思维.经常一题多解，可以锻炼思维能力，扩大视野，提高解题的灵活性.

参考文献

1 李泓斌.对两道高考题的分析及引发的思考.中学物理,2009,29(13):40