物理解题中的近似方法

杨国平

(绍兴市第一中学 浙江 绍兴 312000)

在解决物理问题(观察现象、进行实验、构建模型、推导规律等)时，为了分析、认识研究对象的本质属性，需要突出问题的主要方面，忽略某些次要因素，进行近似处理.近似方法是研究物理学的基本方法之一，有着广泛的应用.善于对实际问题进行合理的近似处理，是从事创造性研究的重要能力之一，也是物理学和数学的显著区别之一.下面从数学、图像及估算3方面加以阐述.

1 数学近似

1.1 抓主略次

两个相同量纲的物理量相加减，若相差悬殊，则可留大去小，简化运算过程，得到的数量级一定是正确的.

【例1】 欲测电阻R的阻值，现有几个标准电阻、一个电池和一只未经标定的电流表A，连成图1所示的电路.第一次与电流表并联的电阻r为r1=50.00 Ω，电流表的示度为n1=3.9格；第二次r改用r2=100.00 Ω，电流表的示度为n2=5.2格；第三次r改用r3=10.00 Ω，同时将待测电阻R换成一个20.00 kΩ标准电阻，结果电流表的示度为n3=7.8格.已知电流表的示度与所通过的电流成正比，求电阻R的阻值.

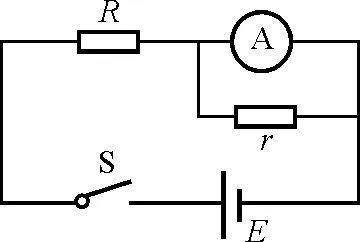
图1

解析:设电源电动势为E，内阻为r′，电流表内阻为Rg，与电流表每格对应的电流为I0，根据闭合电路欧姆定律，有

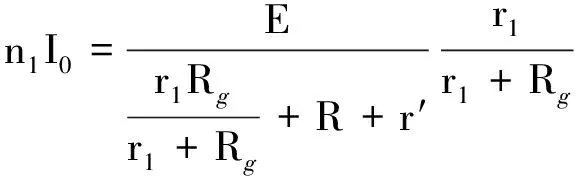
(1)

(2)

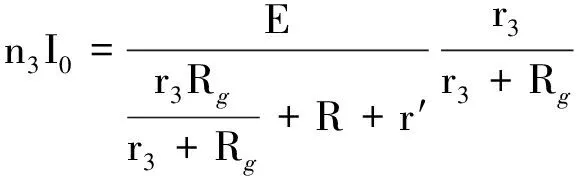
(3)

由第三次测量数据，当r减小时电流表偏转格数却增大，推知总电流必然增加了，由此推知R>20 kΩ.因此，Rg与r的并联值比R小多了，电源内阻r′完全可以忽略不计，故以上三式可近似为

(4)

(5)

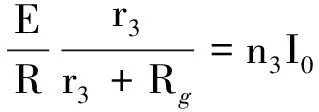
(6)

联立并代入数据解得

R=120 kΩ

1.2 高阶小量近似

物理问题最后往往表征为数学关系式，在涉及到多项式时，经常(尤其是在简谐运动中)用到以下的近似处理(1+x)n=1+nx(x≪1) .其依据就是根据二项式定理展开，略去高阶小量所得.

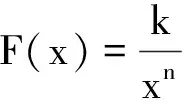
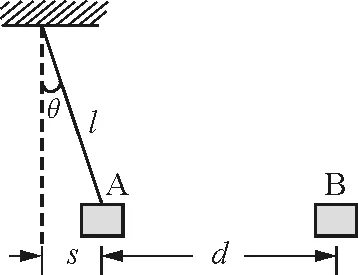
图2

解析:对A分析，设其质量为m，悬挂的线长为l，平衡时线与竖直方向的夹角为θ，则有

mgtanθ=F

(7)

又

代入式(7)得

(8)

右移Δx后，有

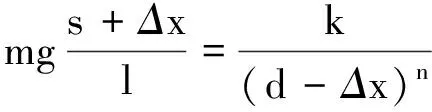
(9)

而

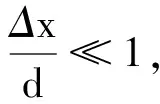
代入式(9)得

(10)

联立式(8)、(10)有

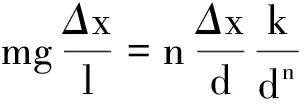
即

化简后有

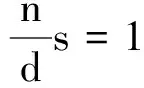
代入数据得

n= 4

【例3】如图3所示，用弹性绳制作对称的轻网，网边缘固定在水平轴环上，半径R等于弹性绳的原长，如果一位体操运动员静止地躺在网中心处，网被压弯的深度为d,问体操运动员从多高处无初速落下，将使网压弯的最大深度为2d? (体操运动员的身高、深度d都比网半径R小得多)

图3 图4

解析： 设网由n根成辐射状的弹性绳编织而成，每根绳的劲度系数均为κ，当网中心下陷x(≪R)时，运动员受到的弹力方向竖直向上，大小

F=nF1sinθ

(11)

由图4可知

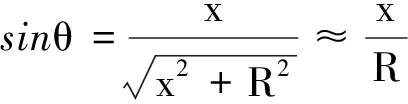
每根绳上的弹力

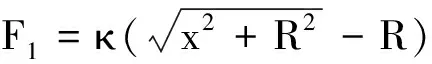
因为

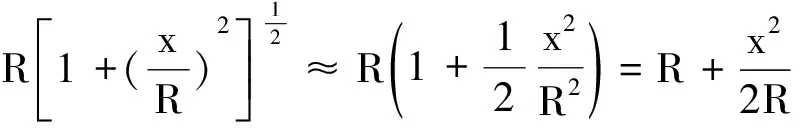
代入式(11)后得

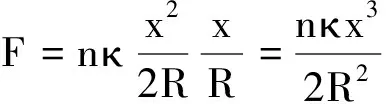
静躺时x=d，由受力平衡得

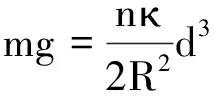
(12)

当运动员从h高处落下时，能使网中心下陷2d，此时每根弹性绳具有的弹性势能

由机械能守恒定律

(13)

联立式(12)、(13)解得

h= 2d

1.3 小角度近似

对于小角度问题(一般认为θ<5°)，经常用到的近似处理是sinθ≈ tanθ≈θ，此处θ的单位是弧度(rad).该结论最典型的应用就是处理几何光学的近轴光线，在运用微元法求解相关问题时，也经常用到这一近似.

【例4】 如图5所示，菲涅耳双棱镜的折射率为n，折射棱角为α(α≪1)，位于对称轴上的单色光缝S(波长为λ)与棱镜相距a，观察屏与棱镜相距b，求屏上干涉条纹的间距.

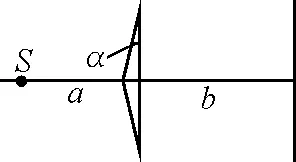
图5

图6

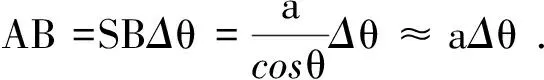
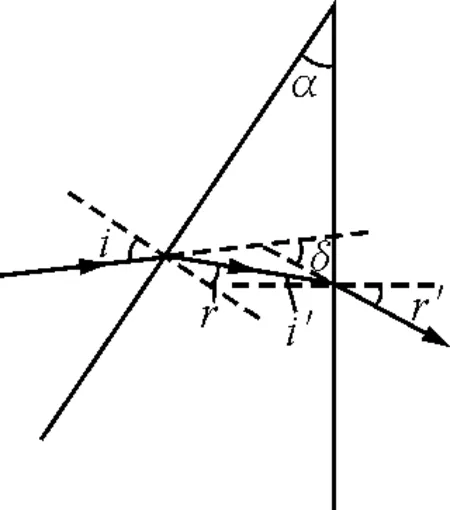
图7

先讨论折射光线相对于入射光线的偏向角δ，如图7所示，设光线在第一界面的入射角和折射角分别为i和r，据折射定律有

sini=nsinr

在第二界面，有

nsini′=sinr′

对于小角度，可简化为

i=nrni′ =r′

由图7可知δ=(i-r)+(r′ -i′) ，因r+i′ =α，则

δ=(i+r′)-α=n(r+i′)-α=(n-1)α

结果表明，光线经两次折射后的偏向角与入射角i无关，那么

Δθ′= Δθ

由此

S1B=SB=a

为求S1离开主轴的距离，考虑边缘光线，其偏向角也等于δ，有

S1S≈aδ

则

S1S2=2S1S=2a(n-1)α

干涉条纹的间距

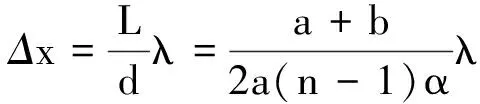
2 图解法近似

图像是描述物理问题的重要方法之一.线性变化的图像具有确定的结果，非线性变化的图像(表现为曲线，更普遍)只能得到一个近似结果.经常用到的处理方法有图像面积(数格子时四舍五入)，图线相交法等等.

【例5】 如图8所示，光滑水平面上静止着一个弹簧振子，其固有周期为4 s .距离振子右侧6 m远处有一光滑曲面，顶端离地高度h=0.2 m .现将振子由O点位置缓缓向左平推2 m，放手的同时，让在曲面顶端的等质量的小物块无初速地滑下，它经过1.5 s到达曲面的底端B点处，之后的某时刻两物体相碰后粘在一起.求碰后振子能达到的最右端位置.(取g=10 m/s2)

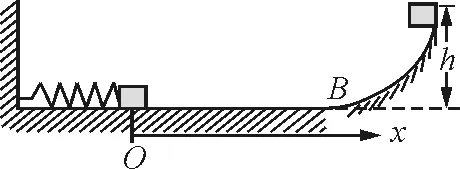
图8

解析：两物粘合后仍是一个弹簧振子，做简谐运动.平衡位置仍在原点O处，题目要求确定其振幅A,先得确定两物在何处相碰.以振子静止位置O为原点，建立图8所示坐标系，其运动规律为

x=Acos(ωt+φ)

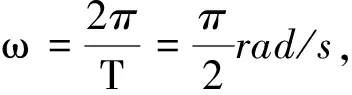
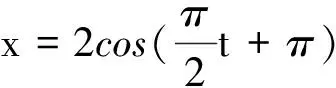
x= 6 - 2t

(14)

统一时间起点后，振子的运动规律应写为

(15)

两物体相碰时x坐标相同，宜采用图解法来解决.在位移图像上作出式(14)的直线和式(15)的正弦曲线，如图9所示，读得交点坐标

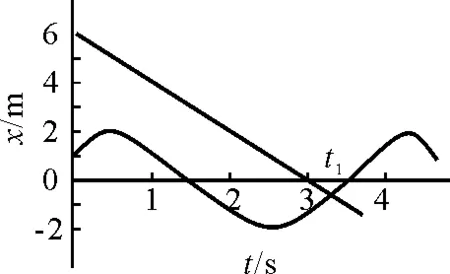
图9

代入式(14)得

x1= -0.6 m

即两物体将在O点左侧0.6 m处相碰.

碰撞过程动量守恒，为此需先求出碰前振子的速度

代入数据

把t1=3.3 代入上式得

v1= 3 m/s

方向向右.

如图10，两物体相向碰撞过程中，有

mv1-mv2= 2mv

图10

解得碰后的共同速度v=0.5 m/s，之后合体在向右运动到最右端的过程中，据机械能守恒，有

(16)

其中

代入式(16) 解得

A=0.75 m

即振子能到达的最右位置在O点的右侧0.75 m处.

3 物理(估算类)近似

对题给条件作合理的简化，再把实际问题抽象为物理模型，是一种近似处理.估算类问题是物理近似的典型.世界上第一颗原子弹爆炸时，费米向空中撒了一把碎纸片，就估算出了原子弹的爆炸当量，可谓是运用近似方法的杰出典范[1].

【例6】 估算在室温下，空气分子之间的平均距离.

解析：根据分子动理论，固体和液体的分子间距跟它们分子本身的线度差不多，而气体分子间的距离则比分子线度大得多.为定量计算，需先建立一个模型，把待研究的气体空间分割为若干个小立方体(这样计算得以最简化)，每个立方体对应于一个分子占据的空间，分子处在立方体的中心.这样，两分子之间的距离就等于小立方体的边长了.

取1 mol空气作为研究对象，在室温下它非常接近于标准状况，气压p≈1×105Pa，温度T≈300 K，由克拉伯龙方程pV=nRT得

代入数据得

V=0.025 m3

因为1 mol气体含有的个数为

NA=6×1023

则每个气体分子所占据的空间体积

小立方体的边长

则分子间距

d=l= 4×10-9m

参考文献

1 周小奋.费米问题三例.物理通报，2011(5)：85