一类广义Vandermonde矩阵的求逆问题＊

刘思洪

（湖州师范学院 理学院，浙江 湖州 313000）

一类广义Vandermonde矩阵的求逆问题＊

刘思洪

（湖州师范学院 理学院，浙江 湖州 313000）

Vandermonde矩阵是矩阵理论中一个重要的矩阵类型，它的许多广义形式在处理矩阵问题时能起到关键的作用．当子块Di的阶数li比较大时，利用分块矩阵法给出了一类广义Vandermonde矩阵D的求逆方法及其逆矩阵的分块结构表达式．

广义Vandermonde矩阵；分块矩阵；逆矩阵

MSC 2000：32A30 32 H02

0 引言

Vandermonde矩阵是矩阵理论中一个重要的矩阵类型，它有着许多相关的广义形式，诸如Cauchy－Vandermonde矩阵、合流-Vandermonde矩阵等［1，2］，在处理一类矩阵问题以及线性方程组等相关问题上都涉及到 广义Vandermonde矩阵的求逆，因而弄清该类广义Vandermonde矩阵的逆矩阵的结构表达式是非常有必要的．对于广义Vandermonde矩阵求逆一般是采用构造插值多项式建立递推关系，然而当子块Di的阶数比较大时，求逆的递推关系不易建立．本文利用分块矩阵的办法给出了一类特殊的广义Vandemonde矩阵的求逆方法及其逆矩阵的分块形式．

1 相关概念

定义1 设n阶方阵D＝［D1，D2，…，Dk］，其中1≤k≤n，

为n×li矩阵，λi为复数，li为自然数且当p＜q时，规定0．矩阵D称为n阶广义Vandermonde矩阵，Di称为D的li阶Vandermonde子块，i＝1，2，…，k．

特别地，当k＝n，li＝1（i＝1，2，…，k）时，D也称为n阶Vandermonde矩阵，记为D0，它可以表示为一个n阶置换矩阵与常规n阶Vandermonde矩阵的乘积，并且容易得到n阶广义Vandermonde矩阵D非奇异［1］．

定义2 对任意自然数n，形如互不相等时，

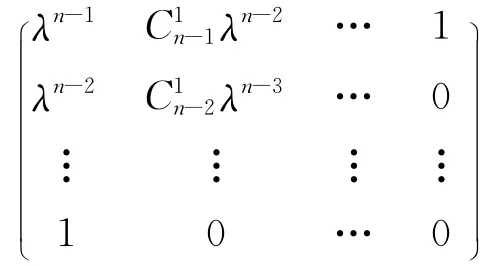
的n阶矩阵称为关于λ的n阶完全广义Vandermonde矩阵，记为Tn（λ）．

定义3［1］设A∈Cm×n，如果存在B∈Cn×m使得BA＝En，则称A是左可逆的，其中Cm×n表示复数域C上所有m×n矩阵构成的集合，En表示n阶单位矩阵，并称B为A的一个左逆．A的左逆一般不惟一，记

命题1［1］设A∈Cm×n，则A是左可逆 ⇔m≥n且rank（A）＝n，即A是列满秩的．

命题2［1］设A∈Cm×n是左可逆的，A的相抵标准形为其中P为m阶可逆方阵，那么，其中F可以是任意n×（m－n）矩阵．

2 主要结论

对于n阶广义Vandermonde矩阵D的li阶Vandermonde子块Di，将Di作分块的自然分块，其中，称为Di

于是可得：

定理1 关于λ的n阶完全广义Vandermonde矩阵Tn（λ）非奇异，并且可表示为如下形式：其中

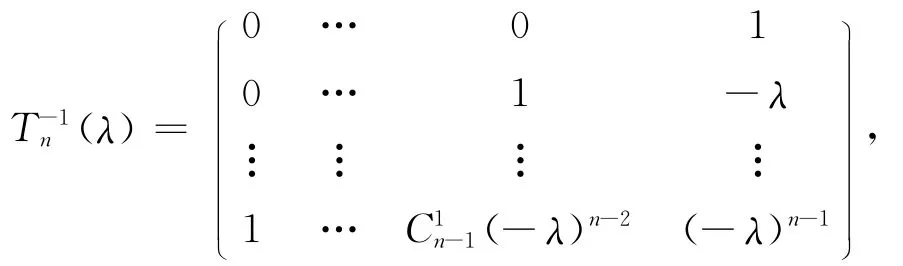
证明 对于任意自然数m，作m次多项式

它的前n－li－m个分量为0，1≤m≤n－li；Yi的（t，s）元为显然矩阵［Xi，Yi］正好是关于其第一行元素的左平移矩阵，即［Xi，Yi］的结构完全是由［Xi，Yi］的第一行确定的，而［Xi，Yi］的第一行的后面li＋1个分量正好可由多项式的系数确定．

定理2 矩阵Zi，Ti，Xi，Yi，i＝1，2，…，k满足：

（i）（n－li）阶方阵Xi是非奇异的，且Xi的逆矩阵可表示为如下形式：

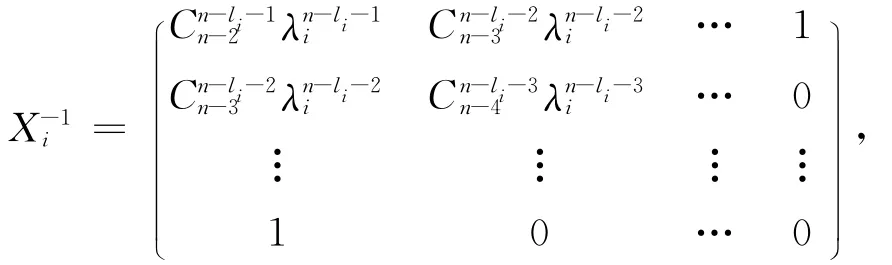
证毕．

由上述定理3可知，只要将满足（ii）、（iii）条件的Bi求出，那么就可以得到Qi，从而就可以求出D－1．为此，以MiNj为子块作矩阵

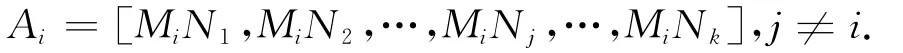
以LiNj为子块作矩阵

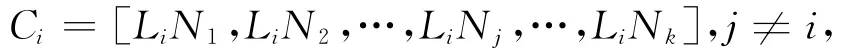
其中Ai、Ci分别是n－li阶方阵及li×（n－li）矩阵，i＝1，2，…，k．

定理4 （n－li）阶方阵Ai是非奇异的，并且Bi＝－，i＝1，2，…，k．

证明 由于

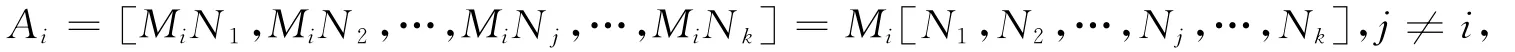
故R（Ai）≤R（Mi）；另一方面，令

由于Ti（i＝1，2，…，k）都是非奇异的，故准对角矩阵Ri也是非奇异的，但Ai是非奇异，故n－li阶方阵Ki非奇异．

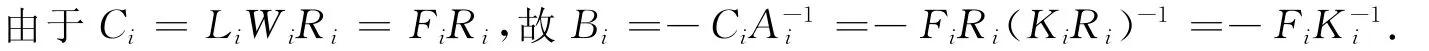
证毕．

注 在实际计算Bi的过程中，应用推论2要比定理4方便些．

［1］陈景良，陈向晖．特殊矩阵［M］．北京：清华大学出版社，2000：162～167，462～482．

［2］徐仲．范德蒙矩阵类的快速算法［M］．西安：西北工业大学出版社，1997：26～32．

MSC 2000：32A30 32H02

The Inverse Problem of Generalized Vandermonde Matrix

LIU Si-hong
（School of Science，Huzhou Teachers College，Huzhou 313000，China）

The Vandermonde matrix is an important type of matrix in matrix theory，and many of its generalized forms are playing a key role in processing matrix problems．This paper provides the method of inverse of generalized Vandermonde matrix D and the block structure expression of its inversed matrix by using block matrices when the order number liof block matrix Diis comparatively large．

generalized Vandermonde matrix；block matrix；inversed matrix

O175．14

A

1009-1734（2011）02-0005-07

2011-03-07

刘思洪，讲师，从事算子理论研究．