广义全酉矩阵和广义（反）全Hermite矩阵＊

方玲凤，蔡 静

（湖州师范学院 理学院，浙江 湖州 313000）

广义全酉矩阵和广义（反）全Hermite矩阵＊

方玲凤，蔡 静

（湖州师范学院 理学院，浙江 湖州 313000）

运用特殊矩阵理论，推广了全酉矩阵和（反）全Hermite矩阵概念，给出了广义全酉矩阵和广义（反）全Hermite矩阵的定义，研究了广义全酉矩阵和广义（反）全Hermite矩阵的基本性质，得到了一些相关推论，并揭示了广义全酉矩阵和广义（反）全Hermite矩阵的内在联系．

广义全酉矩阵；广义全Hermite矩阵；广义反全Hermite矩阵

MSC 2000：15A09

0 引言

特殊矩阵是线性代数的重要组成部分，作为一种基本的数学工具，在数学学科及应用科学领域（如数值分析、优化理论、微分方程、概率统计、现代经济数学等）都有着广泛的应用［1～2］．特殊矩阵的类型有很多，如酉矩阵、Hermite矩阵、Hankel矩阵、Toeplitz矩阵、M-矩阵、H-矩阵等，这些特殊矩阵都有着各自良好的性质，这些性质在经济学、物理学、工程等许多应用学科中有着广泛的应用，因此对特殊矩阵的性质进行研究具有重要的意义．

目前，关于酉矩阵和Hermite矩阵的性质研究已较为广泛和深入［3～6］．在上述研究工作的基础上，文献［7］对酉矩阵和Hermite矩阵概念进行了推广，给出了拟酉矩阵与拟Hermite矩阵的定义及基本性质．文献［8］给出了强酉矩阵的概念，并讨论了它的相关性质．文献［9］～［11］探讨了次酉矩阵、次Hermite和反次Hermite矩阵的特征值、次特征值，以及各类矩阵之间的关系．文献［12］给出了广义次酉矩阵的定义，研究了广义次酉矩阵的性质．文献［13］、［14］研究了广义酉矩阵和广义（反）Hermite矩阵的性质及其相互关系．文献［15］～［17］对全转置矩阵与全正交矩阵概念做了复数域上的推广，定义了共轭全转置矩阵、（反）全Hermite矩阵、左酉矩阵、右酉矩阵以及全酉矩阵，并讨论了其性质及相互关系．

鉴于现有的研究成果，尚未拓展到更广泛的广义全酉矩阵和广义（反）全Hermite矩阵，而上述矩阵相对于全酉矩阵和（反）全Hermite矩阵，有着许多特殊的性质，因此对其进行系统、深入的研究，有助于进一步丰富特殊矩阵的相关理论，深化、拓广其应用．

1 预备知识

文中，C和R分别表示复数集与实数集，Cm×n表示m×n复矩阵集合，det A表示复方阵A的行列式，表示det A的共轭，｜det A｜表示det A的模、AT、A0、A－0分别表示n阶矩阵A的共轭矩阵、转置矩阵、全转置矩阵、共轭全转置矩阵，A＊表示A的余子阵，I、J分别表示单位矩阵和次单位矩阵．文中所提到的矩阵，若无特别声明，均指复矩阵．

定义1［17］设n阶矩阵

2 广义全酉矩阵的定义与性质

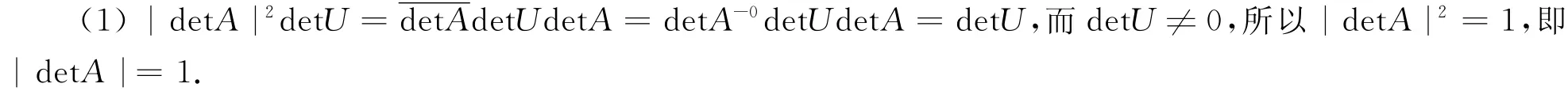
（2）因（A－0）－0U－1A－0＝A（A－0UA）－1A－0＝AA－1U－1（A－0）－1A－0＝U－1，所以A－0∈GU－1．

因（A－1）－0UA－1＝ （A－0）－1（A－0UA）A－1＝U，所以A－1∈GU．

因（A＊）－0UA＊＝ （（det A）A－1）－0U（det A）A－1＝｜det A｜2（A－1）－0UA－1＝U，所以A＊∈GU．

推论1［17］设A是n阶全酉矩阵，那么

（1）A的行列式的模｜det A｜＝1；

（2）A－0、A－1、A＊都是全酉矩阵．

定理2 若n阶矩阵A、B∈GU，且A、B是可交换的，则AB∈GU．

证明 （AB）－0UAB＝A－0B－0UAB＝A－0B－0UBA＝U，所以AB∈GU．

推论2［17］设n阶矩阵A、B是全酉矩阵，A、B是可交换的，则AB是全酉矩阵．

定理3 设A、B均为n阶可逆复矩阵，非奇异矩阵U∈Cn×n，存在Q∈GU，使A＝BQ，且B、Q是可交换的，则A－0UA＝B－0UB．

证明 因A＝BQ，Q－0UQ＝U，又B、Q是可交换的，所以

定义3 设A∈Cn×n，如果存在非奇异矩阵U∈Cn×n．使得A－0UA＝U，则称A是由U确定的广义全酉矩阵，记这种广义全酉矩阵的集合为GU．

注2 当U＝I时，由U确定的广义全酉矩阵即为全酉矩阵．

定理1 设A∈GU，则

（1）A的行列式的模｜det A｜＝1；

（2）A－0∈GU－1，A－1∈GU，A＊∈GU．

证明 因为A∈GU，所以A－0UA＝U，从而

3 广义（反）全Hermite矩阵的定义与性质

定义4 设A∈Cn×n，如果存在非奇异矩阵U∈Cn×n，使得A－0U＝UA（或A－0U＝－UA），则称A是由U确定的广义全Hermite矩阵（或广义反全Hermite矩阵）．

记这种广义全Hermite矩阵的集合为U＋，广义反全Hermite矩阵的集合为U－．

显然，当U＝I时，由U确定的广义全Hermite矩阵是全Hermite矩阵；由U确定的广义反全Hermite矩阵是反全Hermite矩阵．

定理8 设A、B∈U＋，k∈R，则

（1）kA，A±B∈U＋；

（2）AB±BA∈U＋；

（3）AB∈U＋．

证明 （1）因A、B∈U＋，故（A＋B）－0U＝A－0U＋B－0U＝UA＋UB＝U（A＋B），即A＋B∈U＋．同理可证A－B，kA∈U＋．

（2）因A、B∈U＋，故（AB＋BA）－0U＝A－0B－0U＋B－0A－0U＝UAB＋UBA＝U（AB＋BA），所以AB＋BA∈U＋．同理可证AB－BA∈U＋．

（3）因A、B∈U＋，故（AB）－0U＝A－0B－0U＝A－0UB＝UAB，所以AB∈U＋．

定理9 设A∈U＋，则Ak∈U＋．

证明 因A∈U＋，（Ak）－0U＝A－0A－0…A－0U＝UAk，所以Ak∈U＋．

推论5［17］设A是全Hermite矩阵，那么Ak也是全Hermite矩阵．

定理10 （1）若n阶复矩阵A∈U＋，则det A为实数．

（2）若n阶复矩阵A∈U－，则当n为奇数时，det A为0或纯虚数；当n为偶数时，det A为实数．

证明 （1）因A－0U＝UA，所以

4 广义全酉矩阵与广义（反）全Hermite矩阵的关系

定理11 设A∈Cn×n，若以下3个条件中的任意两个成立，则第3个必成立．

（1）A∈GU；

（2）A∈U＋；

（3）A2＝I．

证明 若（1）、（2）成立，则A－0UA＝U，A－0U＝UA，从而有UA2＝U，而U非奇异，所以A2＝I．即（3）成立．

若（1）、（3）成立，则A－0UA＝U，A2＝I，从而有A－0U＝UA－1＝UA，故A∈U＋．即（2）成立．

若（2）、（3）成立，则A－0U＝UA，A2＝I，从而有A－0UA＝UA2＝U，故A∈GU．即（1）成立．

定理12 设A∈Cn×n，若以下3个条件中的任意两个成立，则第3个必成立．

（1）A∈GU；

（2）A∈U－；

（3）A2＝－I．

证明 若（1）、（2）成立，则A－0UA＝U，A－0U＝－UA，从而有UA2＝－U，而U非奇异，所以A2＝－I．即（3）成立．

若（1）、（3）成立，则A－0UA＝U，A2＝－I，从而有A－0U＝UA－1＝－UA，故A∈U－．即（2）成立．

若（2）、（3）成立，则A－0U＝－UA，A2＝－I，从而有A－0UA＝－UA2＝U，故A∈GU．即（1）成立．

定理13 设A∈Cn×n是广义全酉矩阵，且A2＝I，则

（1）A－1BA为广义全Hermite矩阵的充分必要条件是B为广义全Hermite矩阵；

（2）A－1BA为广义反全Hermite矩阵的充分必要条件是B为广义反全Hermite矩阵．

证明 （1）因A是广义全酉矩阵，故A－0UA＝U，所以A－0＝UA－1U－1．由A－1BA为广义全Hermite矩阵得：

UA－1BA＝ （A－1BA）－0U＝ （A－0）－1B－0A－0U＝ （UA－1U－1）－1B－0A－0U＝UAU－1B－0UA－1．

又因A2＝I，结合上式得B＝U－1B－0U．所以B－0U＝UB，即B为广义全Hermite矩阵．反之亦然．

（2）由A－1BA为广义反全Hermite矩阵得：

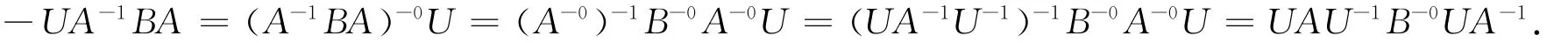
又因A2＝I，结合上式得－B＝U－1B－0U．所以B－0U＝－UB，即B为广义反全Hermite矩阵．反之亦然．

5 小结

本文推广了全酉矩阵和（反）全Hermite矩阵概念，给出了广义全酉矩阵和广义（反）全Hermite矩阵的定义，并研究了广义全酉矩阵和广义（反）全Hermite矩阵的基本性质，揭示了这几类矩阵之间的关系．通过本文的研究，可以更深入地了解这几类矩阵的特殊性质与内在联系，完善其理论，使其能更好地发挥应用价值．

［1］吴昌悫，魏洪增．矩阵理论与方法 ［M］．北京：电子工业出版社，2006：105～135．

［2］陈景良．特殊矩阵 ［M］．北京：清华大学出版社，2003：15～60．

［3］武秀美．对称矩阵与反对称矩阵的若干性质 ［J］．牡丹江大学学报，2010，19（6）：110～111．

［4］LEE J，RIM K S．Properities of symmetric Matrices［J］．Math Anal Appl，2005，3（5）：219～226．

［5］LIU Z Y．Some proprieties of centrosymmetric matrices［J］．Appl Math Comput，2003，141：297～306．

［6］刘兴祥，黄美愿．正定Hermite矩阵的性质 ［J］．西南民族大学学报（自然科学版），2010，36（1）：16～20．

［7］袁晖坪．拟酉矩阵与拟Hermite矩阵 ［J］．数学理论与应用，2001，21（2）：21～25．

［8］陈桂章，刘玉．强酉矩阵及其性质 ［J］．韩山师范学院学报，2008，29（3）：12～16．

［9］袁晖坪．次酉矩阵与次镜像矩阵 ［J］．东北大学学报（自然科学版），2001，33（1）：26～29．

［10］郭华．次正规矩阵、次酉矩阵、次厄米特矩阵及反次厄米特矩阵 ［J］．大学数学，2007，23（2）：174～177．

［11］刘玉波．次Hermite矩阵的某些性质和它的广义逆 ［J］．天津师范大学学报（自然科学版），2006，26（3）：39～44．

［12］刘玉，李佩萍．广义次酉矩阵及其性质 ［J］．高师理科学刊，2007，27（5）：9～15．

［13］赵雪．广义酉矩阵性质的拓广 ［J］．北华大学学报（自然科学版），2004，5（4）：301～302．

［14］王宽社．广义Hermite矩阵及广义酉矩阵 ［J］．陕西科技大学学报，2004，22（1）：117～120．

［15］刘玉，蔡增烁．全酉矩阵及其性质 ［J］．韩山师范学院学报，2009，30（6）：1～5．

［16］卢潮辉．左酉矩阵、右酉矩阵、全酉矩阵及其性质 ［J］．井冈山大学学报（自然科学版），2010，31（2）：5～7．

［17］卢潮辉．全酉矩阵与全Hermite矩阵 ［J］．广东技术师范学院学报，2009，30（3）：78～80．

MSC 2000：15A09

Generalized Full-unitary Matrix and Generalized（skew）Full-Hermite Matrix Center

FANG Ling-feng，CAI Jing
（Faculty of Science，Huzhou Teachers College，Huzhou 313000，China）

By using special matrix theory，we generalize the conceptions of full-unitary matrix and（skew）full-Hermite matrix，give the definitions of generalized full-unitary matrix and generalized（skew）full-Hermite matrix，present the basic properties of generalized full-unitary matrix full-unitary matrix and generalized（skew）full-Hermite matrix，derive some related corollaries and reveal the internal relations of generalized full-unitary matrix and generalized（skew）full-Hermite matrix．

generalized full-unitary matrix；generalized full-Hermite matrix；generalized skew full-Hermite matrix

O151．21

A

1009-1734（2011）02-0036-05

2011-03-04

浙江省自然科学基金项目（Y6110043）；湖州市自然科学基金项目（2010YZ05）．

方玲凤，湖州师范学院理学院2007级本科生，从事特殊矩阵理论研究．