两类分块矩阵的群逆＊

张倍欣，冯茂春

（湖州师范学院 理学院，浙江 湖州 313000）

两类分块矩阵的群逆＊

张倍欣，冯茂春

（湖州师范学院 理学院，浙江 湖州 313000）

当P为退化的幂等矩阵时，我们利用矩阵的秩的性质、分块矩阵的初等变换，以及群逆存在的充分必要条件，讨论了形如其中P为方阵）的两类分块矩阵群逆的存在性．接着，利用初等变换和矩阵1逆的求法，根据矩阵群逆与矩阵3次幂的1逆的关系，最终给出上述两类分块矩阵群逆的一般表示式，并以例子加以说明．

分块矩阵；矩阵的群逆；酉矩阵

MSC 2000：15A24

0 引言

近40多年来，广义逆的理论、应用和计算方法都得到了迅速的发展，这不仅是因为它有很高的理论价值，更重要的是它在数理统计、系统理论、有限马尔可夫过程、差分方程组、人口增长模型和最优化控制等方面都有着广泛的实际应用背景．研究分块矩阵的广义逆及分块算法对许多领域都非常必要，因此分块矩阵的Drazin逆和群逆问题已成为矩阵论研究中的活跃领域，相关文章不断涌现［1～9］．

1979年，S．L．Campbell和Meyer提出了一个开放问题：分块矩阵的

Drazin逆和群逆的表达．这一问题至今尚未完全解决．分块矩阵）的群逆或Drazin逆问题已有讨论［2～4］．S．L．Campbell在文献［1］中提出形为的分块矩阵的Drazin逆表示问题，但人们对此问题的解答至今仍局限在某些特殊条件下［5，6］．本文在整理了一些特殊分块矩阵的群逆表示方法的基础上，利用群逆存在的充分必要条件，讨论形如的两类分块矩阵的群逆的存在性，并给出以上两类分块矩阵的群逆的一般表示．

1 相关概念与引理

定义1 设A∈Cn×n，称满足rank Ak＋1＝rank Ak的最小非负整数k为A的指标，记作Ind（A）＝k．

定义2 设A∈Cn×n，Ind（A）＝k，若X∈Cn×n满足：①AkXA＝Ak；②XAX＝X；③AX＝XA，则称X为A的Drazin逆，记作X＝AD．

定义3 设A∈Cn×n，若X∈Cn×n满足：①AXA＝A；②XAX＝X；③AX＝XA，则称X为A的群逆，记作X＝A＃，即当k＝1时的Drazin逆为群逆．

定义4 设A∈Cm×n，则满足AXA＝A的矩阵X∈Cm×n称为A的｛1｝逆，记作X＝A（1）或X∈｛1｝．

引理1［7］设A∈Cn×n，则A的Drazin逆存在且唯一．

引理2［7］设A∈Cn×n，A为奇异矩阵，则A＃存在的充分必要条件为：Ind（A）＝1，且A＃唯一．

引理3［7］设A∈Cn×n，Ind（A）＝1，则A＃＝A（A3）（1）A．

引理4［8］设A∈Cn×n，A有特征值λ1，λ2，…，λn，它们按规定的次序排列，则存在酉矩阵U，使得U＊AU为上三角矩阵，其中主对角线上的元素有序．

引理5［9］设P2＝P，P∈Cn×n，且rank（P）＝r≠0，则存在酉矩阵U，使得

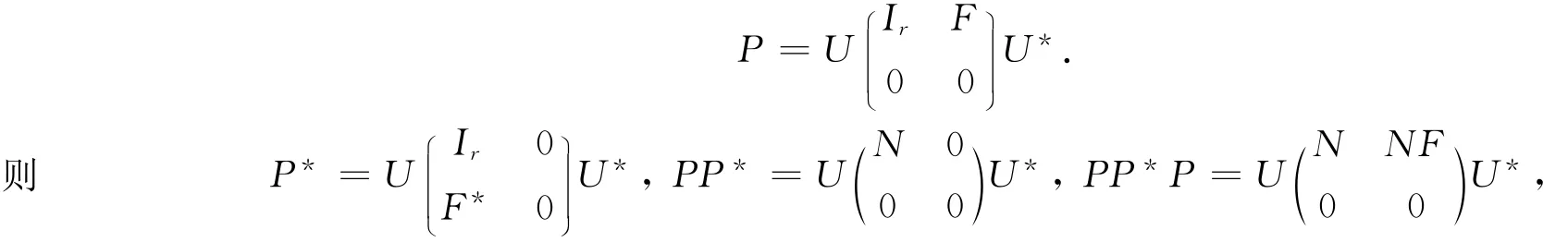
其中N＝Ir＋FF＊可逆，（PP＊）＃，（PP＊P）＃存在．

2 结论

［1］CAMPBELL S L．The Drazin inverse and systems of second order linear differential educations［J］．Linear and Multilinear Algebra，1983，14（2）：195～198．

［2］MEYER C D，ROSE N J．The index and D razin inverse of block triangularmatrices［J］．SIAM J Appl Math，1977（33）：1～7．

［3］曹重光．体上分块矩阵群逆的某些结果 ［J］．黑龙江大学学报（自然科学版），2001，18（3）：5～7．

［4］刘玉，曹重光．体上某些分块矩阵的Drazin逆 ［J］．黑龙江大学学报（自然科学版），2004，21（4）：112～114．

［5］卜长江．关于体上分块矩阵的群逆 ［J］．数学杂志，2002，35（4）：49～52．

［6］CASTRO-GONZALEZ N，DOPAZO E．Representation of the Drazin inverse for a class of block matries［J］．Linear Algebra Appl，2005，400：253～269．

［7］王国荣．矩阵与算子广义逆 ［M］．北京：科学出版社，1994：48～66．

［8］缪建铭．关于分块矩阵的Drzain逆的一些结果 ［J］．上海师范大学学报，1989，18：25～31．

［9］马元倩，曹重光．分块矩阵的群逆 ［J］．哈尔滨师范大学学报，2005，21（4）：7～8．

MSC 2000：15A24

The Group Inverse of Two Classes of Block Matrix

ZHANG Bei-xin，FENG Mao-chun
（School of Science，Huzhou Teachers College，Huzhou 313000，China）

When P is singular idempotent matrix，using the properties of matrixes rank，elementary transformation of block matrix，and necessary and sufficient condition for the existence of group inverse，we discuss the existence of group inverse of block matrix shaped like M．Next，using elementary transformation and calculation method for 1 inverse of matrix，according to the relation of matrices＇group inverses and 1 inverse of 3 power of matrix．Finally we give the general expression of the two kind of block matrixes＇group inverse，and illustrate it with examples．

block matrix；group inverse of matrix；stepped matrix

O151．21

A

1009-1734（2011）02-0041-05

2011-03-25

湖州师范学院教改重点项目（2008JY006）．

张倍欣，湖州师范学院理学院2007级本科生，从事矩阵代数研究．