一类广义混合变分不等式组解的强收敛定理＊

史 杰，何中全

（西华师范大学 数学与信息学院，四川 南充 637009）

一类广义混合变分不等式组解的强收敛定理＊

史 杰，何中全

（西华师范大学 数学与信息学院，四川 南充 637009）

研究了Banach空间中一类广义混合变分不等式组问题，引进了一种新的迭代算法，研究了由迭代算法生成的序列的收敛性，并得到了这类变分不等式组解的强收敛定理，从而推广和改进了相关文献的一些工作．

变分不等式组；迭代算法；投影算子；强收敛

MSC 2000：47H10

1 准备知识

记上面的GMEPS的解集为GMEPS（F，G，A，B）．

当F＝G，A＝B，F（x，y）＝f（x，y）＋φ（y）－φ（x），η（y，x）＝y－x时，上面的GMEPS问题变为GMEP问题，即求x∈C，使得f（x，y）＋φ（y）－φ（x）＋〈y－x，Ax〉≥0，∀y∈C．GMEP问题在文献［2］和［3］中已经被研究．

下面给出本文所需的一些引理．

引理1［1］设E是严格凸且光滑的实自反Banach空间，C是E中非空闭凸集，令x∈E，那么对任意设E是Banach空间，E＊是其对偶空间，正规对偶映射J∶E→2E＊如下定义：的y∈C，有：

2 主要结果

在本节，我们将引进一个新的迭代算法，研究由此生成的序列的收敛性，得到了变分不等式组解的强收敛定理．相关工作推广和改进了文献［2］和文献［3］的相关结果．

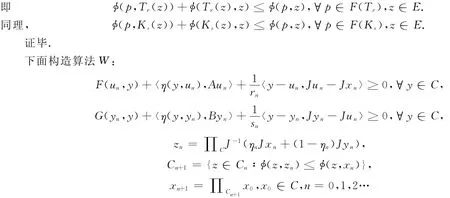
定理5 C是一致光滑且自反的实Banach空间中非空闭凸集．F，G∶C×C→R，满足条件（A1）～（A4）．映射η∶C×C→C满足条件（B1）～ （B3），A，B∶C→E＊是η－单调映射．｛xn｝是由算法W生成的序列．其中｛rn｝，｛sn｝是［e，＋∞）上序列，e＞0，x0∈C0＝C，设GMEPS（F，G，A，B）≠Φ，则｛xn｝强收敛到x＊∈GMEPS（F，G，A，B）．

证明 下面分四步进行证明．

第一步：证明算法W生成的序列是良定的，且GMEPS（F，G，A，B）⊆Cn．

易知Cn是C中非空闭凸集，则｛xn｝是良定的．设p∈GMEPS（F，G，A，B），由引理4和引理1得：

定理6 C是一致光滑且自反的实Banach空间中非空闭凸集．F，G∶C×C→R，满足条件（A1）～（A4）．映射η∶C×C→C满足条件（B1）～（B2），A，B∶C→E＊是η－单调映射，g∶E→C是连续映射．｛xn｝是由算法Q生成的序列．其中｛rn｝，｛sn｝是［e，＋∞）上序列，e＞0，x0∈C0＝C，设GMEPS（F，G，A，B，g）≠Φ．则｛xn｝强收敛到x＊∈GMEPS（F，G，A，B，g）．

证明方法同定理5．

［1］ZEGEYE H，Eric U，OFOEDU E U，et al．Convergence Theorems for Equilibrium Problem，Variotional Inequality Problemand Countably Infinite Relatively Quasi-nonexpansive Mappings［J］．Appl Math Comput，2010，54：5．

［2］ZHANG S S．Generalized mixed equilibrium problem in Banach space［J］．Applied Msthematics and Mechanics，2009，30：1105～1112．

［3］KUMAM W，JAIBOON C，KUMAM P，et al．A Shrinking Projection Method for Generalized Mixed Equilibrium Problems，Variational Inclusion Problems and a Finite Family of Quasi-Nonexpansive Mappings［J］．Hindawi Publishing Corporation Journal of Inequalities and Applications，2010，2010：1～25．

［4］KAMIMURA S，TAKAHASHI W．Strong Convergence of Proximal-type Algorithm in a Banach Space［J］．SIAM J，2002，13，938～945．

［5］ZEGEYE H，ERIC U，OFOEDU E U，et al．Convergence Theorems for Equilibrium Problem，Variotional Inequality Problemand Countably Infinite Relatively Quasi-nonexpansive Mappings［J］．Appl Math Comput，2010，54：5．

MSC 2000：47 H10

Strong Convergence Theorem for a System of Generalized Mixed Variational Inequality

SHI Jie，HE Zhong－quan
（School of Mathematics and Information，China West Normal University，Nanchong 637009，China）

This paper，which introduces a new iteration algorithm and researches into the convergence of iterative sequence generated by the algorithm，is devoted to studying a new system of generalized mixed variational inequality in Banach spaces，from which we get the strong convergence theorems of the solution for this system of generalized mixed variational inequality．The results obtained in this paper extend corresponding works of others．

system of variational inequality；iteration algorithm；projection operator；strong convergence

O177．91

A

1009-1734（2011）02-0030-06

2011-03-04

四川省教育厅2009年度重点课题基金资助项目（07ZA123）．

史杰，2009级在读硕士，从事非线性分析研究．