薄片炸药与固体靶冲量耦合的计算模型＊

卢 强，王占江，刘晓新，郭志昀，吴玉蛟

（西北核技术研究所，陕西西安710024）

薄片炸药与固体靶冲量耦合的计算模型＊

卢 强，王占江，刘晓新，郭志昀，吴玉蛟

（西北核技术研究所，陕西西安710024）

薄片炸药可用于模拟强脉冲X射线辐照下空间结构的响应，其与固体靶的冲量耦合作用是进行模拟载荷设计的基础。本文中基于有限元模拟技术，研究不同直径薄片炸药的边界稀疏作用和安装支座的反射作用对薄片炸药与固体靶冲量耦合的影响，结果表明：边界稀疏作用对薄片炸药的比冲量起到减弱的作用，由边界稀疏作用引起的薄片炸药比冲量的变化量和薄片炸药直径的倒数近似成线性关系；薄片炸药安装支座的反射作用对薄片炸药的比冲量起到增强的作用，由支座反射作用引起的薄片炸药比冲量的变化量和薄片炸药直径的平方近似成反比；随着薄片炸药直径的增加，薄片炸药比冲量趋于定值，边界稀疏作用和支座反射作用可以忽略；存在一个临界直径，当薄片炸药的直径为临界直径时，薄片炸药的边界稀疏作用和支座反射作用达到平衡，其比冲量大小和薄片炸药的直径为无穷大时的比冲量值相等。

爆炸力学；冲量耦合；比冲量；薄片炸药

高空核爆炸约有70%～80%的能量以X射线的形式释放，当强脉冲X射线辐照到空间结构体表面时，在空间结构体迎光面表层产生能量沉积，并引起表层材料熔化、汽化，从而引起物质的反冲喷射，形成作用在空间结构体上的汽化反冲冲量，继而引起空间结构的动态响应、破坏或失效，这属于脉冲X射线对空间结构的力学效应［1－2］。在实验室内可以采用脉冲电子束辐照、激光辐照等模拟脉冲X射线的辐照效应［2－3］，采用光敏炸药、薄片炸药或柔爆索等模拟脉冲X射线引起空间飞行器的结构响应［3］。

R.A.Benham［4］和W.G.Rivera等［5－6］发展了一种通过闪光起爆光敏炸药的加载技术，可以实现大面阵同时加载，能较好地模拟X射线辐照空间结构壳体的脉冲载荷特征，其技术难点在于光敏炸药的安全控制以及喷涂工艺。W.E.Alzheimer等［7］、B.W.Franklin［8］、H.E.Lindberg等［9］和S.W.Kirkpatrick等［10］通过对按照一定规律离散的薄片炸药条一端起爆的方式实现对结构的滑移爆轰加载，从而模拟脉冲X射线辐照下的载荷。毛勇建等［11－13］对薄片炸药加载技术进行了较为系统的研究，从数值模拟的角度分析了薄片炸药加载的载荷特征以及对X射线力学效应的等效性问题。相比于光敏炸药加载技术，薄片炸药加载技术的优点是安全性高、技术成本较低，但由于炸药的极限爆轰尺寸的限制，较难实现对空间结构载荷均匀性高、低比冲量的加载模拟。赵国民等［14］采用按照一定规律离散分布的铅皮柔爆索一端起爆的方式来模拟脉冲X射线辐照下的载荷。此技术主要是利用柔爆索爆炸产生的飞散铅粒子与空间结构碰撞产生的相互作用，虽然载荷的可设计性强，但同样较难实现对空间结构载荷均匀性高、低比冲量的加载模拟。

无论采用何种方式来模拟X射线力学效应，载荷的比冲量特征都是针对相应空间结构进行加载设计的关键技术参数。目前国内对X射线力学效应的模拟仍主要采用薄片炸药加载来实现［11－13，15－17］。采用薄片炸药模拟脉冲X射线引起空间飞行器结构响应时，需通过一定方式对薄片炸药进行离散以满足模拟脉冲X射线辐照空间结构产生的反冲冲量的需要。对薄片炸药的离散加载设计的前提是要对薄片炸药与固体靶的冲量耦合作用进行研究。岳晓红等［15］采用薄片炸药与固体靶的冲量耦合作用测量的摆锤结构及薄片炸药比冲量标定方法，但起爆炸药条、薄片炸药边界的稀疏作用对比冲量的影响没有提及。林鹏等［16］采用直线运动式冲量探头测得了0.4mm厚薄片炸药的比冲量，实验中薄片炸药由柔爆索引爆，并未考虑起爆方式对薄片炸药比冲量的影响，在数值模拟研究中没有考虑薄片炸药边界稀疏作用。郭志昀等［17］对0.4和0.5mm厚薄片炸药与固体靶的冲量耦合特性进行研究，指出薄片炸药边界稀疏作用和安装支座反射冲量对比冲量测试具有影响，但未进一步讨论。

本文中基于有限元模拟技术，考虑不同直径薄片炸药边界稀疏以及安装支座反射冲量对超薄片状炸药与固体靶的冲量耦合作用的影响，建立了薄片炸药与固体靶冲量耦合的计算分析模型。

1 薄片炸药比冲量测试技术

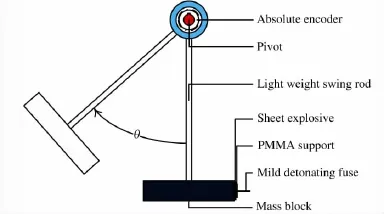
图1 薄片炸药冲量测量装置Fig.1 Impulse measurement apparatus for sheet explosive

2 薄片炸药与固体靶冲量耦合模型

薄片炸药与固体靶冲量耦合作用测试中不同因素对冲量耦合作用的影响主要有：（1）薄片炸药的尺寸效应。薄片炸药冲量测试的理想实验条件是应满足一维应变式的加载，实际情况下难以做到，一般采用具有一定大小的薄片炸药比冲量来代替理想的薄片炸药比冲量，但有限尺寸薄片炸药边界产生的稀疏波会减弱薄片炸药的加载能力，使得测试得到的薄片炸药比冲量偏小；（2）由于柔爆索和薄片炸药都是柔性加载元件，一般需采用1个连接支座过渡，如图2所示。使柔爆索顶端可以垂直顶在薄片炸药表面，以提高薄片炸药起爆的可靠性。薄片炸药起爆后会在连接支座和薄片炸药之间产生1个较高的反射压，同时柔爆索爆炸也会对固体靶产生1个附加冲量，这会使得测试得到的薄片炸药比冲量偏大。基于上述考虑，采用有限元方法，以不同尺寸的连接支座及不同厚度、不同直径的薄片炸药进行数值模拟，分析薄片炸药边界稀疏作用和连接支座冲量反射作用对薄片炸药与固体靶冲量耦合的影响，由此建立薄片炸药比冲量特性的计算模型。

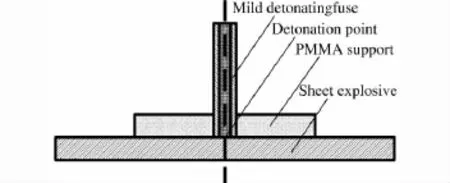
图2 柔爆索起爆薄片炸药的支撑结构Fig.2 Structural support for sheet explosive detonated by mild detonating fuse

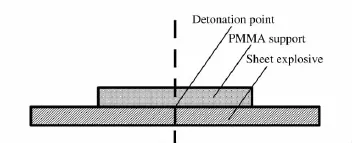
图3 爆索柔起爆薄片炸药的支撑结构的简化模型Fig.3 Simplified model of the structural support for sheet explosive detonated by mild detonating fuse

薄片炸药加载冲击摆的摆锤过程约为10～100μs量级，之后摆锤即可达到恒定速度，而冲击摆的周期为1s量级，可以认为薄片炸药加载摆锤质量块的过程瞬间完成，因此可对冲击摆模型进行简化，只考虑薄片炸药加载质量块的过程，忽略了接触爆炸时质量块产生的塑性变形对冲量的影响。另外柔爆索附加冲量的影响在数值模拟中先不予考虑，在后面分析中再谈及这个问题。由此图2所示的柔爆索起爆薄片炸药的支撑结构可以简化为图3所示的模型。由于结构的对称性，建立1／4有限元模型进行计算，柔爆索和薄片炸药之间的连接座采用有机玻璃材料，质量块采用钢材料，如图4所示。所有模拟中均采用相同的网格尺寸，其中薄片炸药沿厚度方向的网格尺寸为0.1mm。

2.1 边界稀疏波对冲量耦合作用的影响

为考虑薄片炸药与固体靶冲量耦合作用的影响，在计算模型中未对连接支座建模，薄片炸药直接贴敷在质量块表面，起爆点设置在圆形薄片炸药上表面中心位置。选取了厚度δ为0.2、0.3和0.5mm的薄片炸药进行模拟，其直径D为10～60mm。设质量块的质量为m0，薄片炸药爆炸后质量块的稳定运动速度为v，则薄片炸药的比冲量i为：

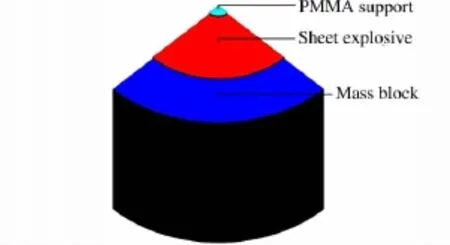
图4 薄片炸药比冲量测试的有限元模型Fig.4 Finite model for measurement of specific impulse for sheet explosive

通过计算，图5给出了仅考虑边界稀疏作用下的薄片炸药比冲量iRA的模拟结果。从图5中可以看出，对应同一直径的薄片炸药，其厚度越大，比冲量也越大。对应同一厚度的薄片炸药，随着直径的增加，比冲量大小趋于恒定值。以1／D 为横坐标、比冲量iRA为纵坐标对图5进行了重新绘制，如图6所示。图6中不同形状的点代表不同厚度薄片炸药比冲量数值模拟结果，直线为对应的比冲量拟合线。可以看出，通过模拟计算给出的薄片炸药比冲量iRA和1／D近似成线性关系（3种厚度薄片炸药比冲量的拟合线性度均在0.996以上），不同厚度薄片炸药比冲量拟合直线的截距代表了对应厚度薄片炸药的极限比冲量值（D 趋于无穷大时的比冲量）。设极限比冲量值为i0（δ），则图6中的拟合直线可以统一写为：

式中：斜率k（δ）为与薄片炸药厚度相关的量，其表示薄片炸药比冲量随着1／D变化的快慢，k（δ）／D代表了稀疏作用引入到薄片炸药比冲量中的大小。从图6可以看出，随着薄片炸药厚度 增加而增加，这说明薄片炸药厚度越大，边界稀疏作用的影响也越大。

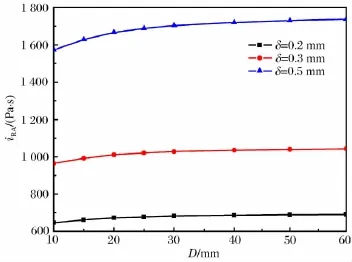
图5 考虑边界稀疏作用下的薄片炸药比冲量iRA随D的变化Fig.5 Specific impulse iRAfor sheet explosive varying with Din consideration of the rarefaction by the border

图6 考虑边界稀疏作用下的薄片炸药比冲量iRA随1／D的变化Fig.6 Specific impulse iRAfor sheet explosive varying with 1／Din consideration of the rarefaction by the border

2.2 连接支座对薄片炸药与固体靶冲量耦合作用的影响

要想防止和解决物流企业财务风险，就必须做好建立、健全企业内部财务控制机制体系的有效措施。物流企业财务内部监控工作建立在企业各项资金预算的基础上，并且符合企业运作的整体利益。企业在充分运用实时财务信息的条件下，应该及时监督和控制公司整体经营目标进展情况。同时，企业需要加强对资金流量加以监控，其目的为确保企业经营目标实现的情况下提升资金使用的效率。

在实际应用中，薄片炸药和固体靶之间需用支座进行连接，安装示意图如图2所示。柔爆索穿过有机玻璃支座中心孔直接顶到薄片炸药上，柔爆索直径为1mm，装药（RDX）的线密度为0.2g／m，柔爆索引爆薄片炸药可近似为点起爆。在数值模拟中忽略了柔爆索附加冲量的作用，把有机玻璃支座和薄片炸药接触面的中心直接设置为起爆点，如图3所示。为对比说明有机玻璃支座对薄片炸药比冲量的影响，采用表1所示的几种工况进行数值模拟。

表1 考虑连接支座反射影响时的模拟工况Table 1 Working condition for simulation in consideration of the reflection by the structural support

图7给出了考虑支座反射和边界稀疏联合作用时和仅考虑边界稀疏作用时的薄片炸药比冲量模拟结果，分别用虚线和实线表示。用iRE表示考虑了有机玻璃支座反射后薄片炸药的比冲量。当考虑支座反射冲量的影响后，iRE大于iRA，并且iRE随D的增加而变小并趋于恒定值，这和仅考虑边界稀疏作用时给出的iRA的变化规律是相反的。值得注意的是随着D的增加，iRE和iRA越来越接近，这说明随着D的增加，无论是薄片炸药的边界稀疏作用还是有机玻璃支座的反射作用都对薄片炸药比冲量测试的影响在减小。定义Δi为：

式中：Δi反映了扣除稀疏作用后有机玻璃支座反射引起比冲量的增加量，d和h分别为有机玻璃支座的直径和厚度。如图7中的灰色区域所示。有机玻璃支座引入薄片炸药与固体靶冲量耦合作用中的总冲量增量设为ΔI，则ΔI可以写为：

考虑有机玻璃支座反射影响时，测试得到的总冲量可写为：

根据式（4）～（5），图8给出了总冲量I和有机玻璃支座引入薄片炸药与固体靶冲量耦合作用中的总冲量增量ΔI随薄片炸药直径的变化规律。可以看出随着D的增加，ΔI变化不大，可近似视为ΔI不随D变化，即ΔI＝ΔI（δ，d，h）。结合式（4），能够得到Δi随着D的变化满足幂指数衰减，且衰减指数为2。由于薄片炸药的边界稀疏作用和有机玻璃支座的反射作用是相互耦合的，同时有机玻璃支座自身的边界也引入了一定的稀疏作用，通过式（3）计算的Δi并不能完全扣除边界稀疏作用造成的影响。若考虑附加柔爆索冲量的影响，可认为近似为点起爆的柔爆索爆炸对质量块的附加冲量为定值，可以附加到ΔI中去考虑，其引起的薄片炸药比冲量的变化符合式（4）的描述。

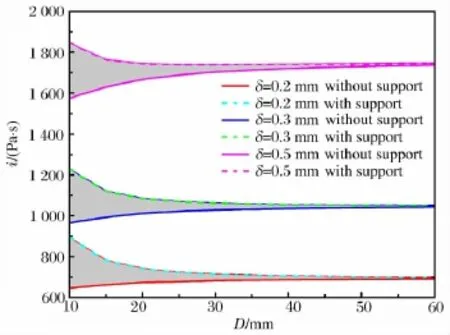
图7 考虑支座反射作用下的比冲量i随D的变化关系Fig.7 Relationship between the specific impulse i and D in consideration of the reflection by the structural support

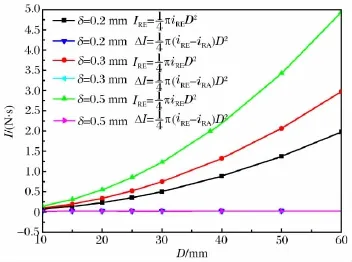
图8 考虑支座反射作用下的冲量I随D的变化关系Fig.8 Relationship between the total impulse I and D in consideration of the reflection by the structural support

2.3 薄片炸药与固体靶冲量耦合的计算模型及分析

从上述数值模拟结果的分析可以知道，随着D的增加，边界稀疏及有机玻璃支座反射作用对薄片炸药与固体靶冲量耦合的影响会减弱，假定边界稀疏和支座反射作用对冲量耦合作用的影响相互独立，结合式（2）～（4）能够给出考虑有机玻璃支座时的比冲量i计算公式：

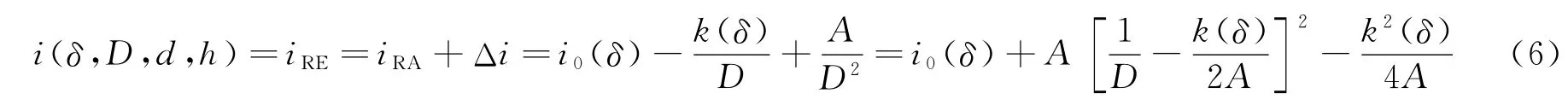
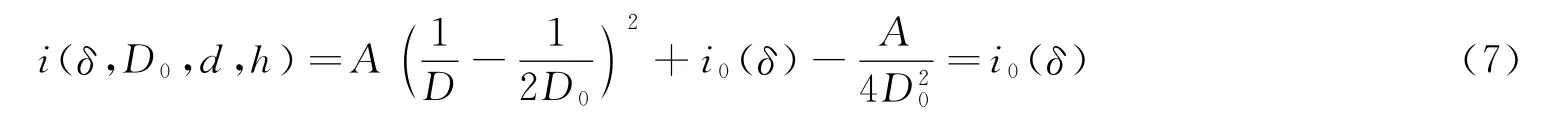
图9 比冲量计算模型的拟合曲线和数值模拟对比Fig.9 Comparison of specific impulse between model fitting results and simulation

现在讨论比冲量i计算模型的适用性，具体结果可见如表2所示。

表2 模型拟合结果和数值模拟结果对比Table 2 Comparison between model fitting results and numerical simulation results

对于δ＝0.2、0.3、0.5mm这3种情况，采用计算模型拟合给出的薄片炸药比冲量近似值i0和i0（δ）十分接近，两者的最大相对误差为0.71%。通过计算模型的拟合曲线给出的临界直径近似值和由数值模拟结果插值给出i0（δ）对应的临界直径D0均随着薄片炸药厚度的增加而变小，但在δ＝0.2，0.3时计算模型给出的误差较大，在δ＝0.5mm时两者给出的结果较为接近。这主要是因为δ＝ 0.5mm时，式（6）表示的关于1／D的抛物线对称轴在2D0＝29.2mm处，当D的模拟区间为10～60mm时，计算结果充分反映了i（δ，D0，d，h）随D先减小而后增大的趋势。当δ＝0.2，0.3mm时，2D0＝103.2，65.0mm，当D的模拟区间为10～60mm时，计算结果只能反映i（δ，D0，d，h）随D减小的趋势，这使得采用计算模型拟合的比冲量曲线误差较大。可见，若能确定D0，则在进行比冲量测试实验时仅用1发实验即可确定薄片炸药的比冲量i0（δ）。但在实际应用中，对一种新配方或新工艺生产的薄片炸药而言，是无法提前确定一个合适的D0进行实验的，那么为了测得某一厚度为δ的薄片炸药的比冲量i0（δ），则需要进行一系列不同直径薄片炸药与固体靶冲量耦合作用的测试实验，以得到反映薄片炸药比冲量随D先减小而后增大现象的测试曲线。

2.4 连接支座直径大小对临界直径的影响

从上述分析可以看出，临界直径D0越小越有利于获得薄片炸药的极限比冲量i0（δ），因此需要通过一定的设计来减小临界直径D0。由于，则减小D0有2种方式：（1）增加k（δ）；（2）降低A（δ，d，h）。对于特定形状的薄片炸药而言，k（δ）只和薄片炸药的厚度有关，其表征的是特定厚度薄片炸药的边界稀疏效应，薄片炸药厚度一定时，k（δ）可视为常数，因此只能通过降低表征反射冲量大小的A（δ，d，h）来减少临界直径k（δ）的大小。在采用7mm×0.5mm尺寸的有机玻璃支座进行薄片炸药与固体靶冲量耦合作用模拟的基础上，增加了5mm×0.5mm和10mm×0.5mm这2种尺寸有机玻璃支座的模拟，薄片炸药厚度取0.5mm。

图10给出了采用不同尺寸有机玻璃支座作用时薄片炸药与固体靶冲量耦合作用的模拟结果。可以看出，随着有机玻璃支座直径d的减少，薄片炸药比冲量值随之减少，这说明支座反射冲量对薄片炸药比冲量的影响降低，反映在式（6）中即A（δ，d，h）也随之降低。当d＝7，10mm时，对应的临界直径D0为14.6和35.7mm。当d＝5mm时，在D为10～60mm的模拟区间内得到的薄片炸药比冲量均小于i0（δ）＝1 770.39Pa·s，则可知D0必小于10mm。利用此组数据结合式（6）可以给出D≈7mm，而通过数值模拟得到的D≈5.7 mm，造成此种现象的主要原因是当薄片炸药直径和有机玻璃支座的直径接近时，薄片炸药边界稀疏作用和支座反射作用耦合作用增大，边界稀疏作用和支座反射作用对冲量耦合作用的影响相互独立的假定不再成立，这造成了计算模型的偏差。上述分析结果证实了通过降低有机玻璃支座的直径d的大小可以有效降低薄片炸药比冲量测试中临界直径D0的大小。

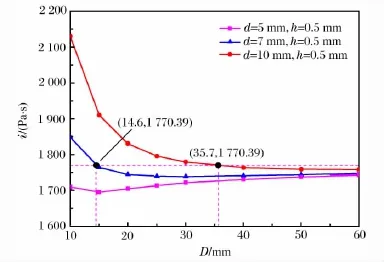
图10 不同尺寸有机玻璃支座作用下比冲量曲线Fig.10 Specific impulses for sheet explosive with different PMMA support sizes

3 结 论

本文中针对薄片炸药与固体靶冲量耦合特性进行了研究，建立薄片炸药比冲量特性的计算模型，该模型对于指导薄片炸药比冲量的测定以及对模拟强脉冲X射线施加到空间结构上的载荷进行理论设计具有一定实用价值。基于分析可以得到以下结论：

（1）薄片炸药边界稀疏对冲量耦合作用起到减弱的效果，其对比冲量测试的影响随着薄片炸药直径的增加而减少，边界稀疏引起的薄片炸药比冲量的减少量和1／D近似成线性关系；

（2）用于连接薄片炸药和柔爆索的支座反射作用对冲量耦合起到增强的效果，其对比冲量测试的影响随着薄片炸药直径的增加而减少，支座反射引起的薄片炸药比冲量的增加量随着薄片炸药直径的增加近似满足幂指数衰减的变化规律；

（3）根据式（6）建立的薄片炸药比冲量计算模型可以知道，薄片炸药比冲量和1／D成抛物线关系，且存在一个薄片炸药的临界直径，当D＝D0时，有i（δ，D，d，h）＝i0（δ）；

（4）临界直径 较小时有利于获得薄片炸药的极限比冲量i0（δ），对于特定厚度和边界形状的薄片炸药，降低连接支座反射冲量的大小可以有效降低临界直径D0。

［1］Longley R W.Analytical relationships for estimating the effects of X－rays on materials［R］.AD－786926，1974.

［2］周南，乔登江.脉冲束辐照材料动力学［M］.北京：国防工业出版社，2002.

［3］毛勇建，邓宏见，何荣建.强脉冲软X光喷射冲量的几种模拟加载技术［J］.强度与环境，2003，30（2）：55－64.Mao Yongjian，Deng Hongjian，He Rongjian.Several simulation techniques of blow－off impulses by intense pulsed cold X－ray［J］.Structure and Environment Engineering，2003，30（2）：55－64.

［4］Benham R A.Preliminary experiments using light－initiated high explosive for driving thin flyer plates［R］.SAND79－1847，1980.

［5］Rivera W G，Benham R A，Duggins B D，et al.Explosive technique for impulse loading of space structures［C］∥The 70th Shock and Vibration Symposium.1999.

［6］Rivera W G.Cosine distributed impulsive loading of a thin aluminum ring by a light initiated high explosive driven flyer plate［C］∥The 77th SAVIAC Shock and Vibration Symposium.2006.

［7］Alzheimer W E，Forrestal M J.Response of a circular elastic shell to moving and simultaneous loads［J］.AIAA Journal，1970，8（5）：970－971.

［8］Franklin B W.Development of a high－energy flexible sheet explosive［R］.AD－786510，1974.

［9］Lindberg H E，Colton J D.Sheet explosive simulation for combined shock and structural response［R］.AFWL－TR－69－124，1970.

［10］Kirkpatrick S W，Hohmes B S.Structural response of thin cylindrical shells subjected to impulsive external loads［J］.AIAA Journal，1988，26（1）：96－103.

［11］毛勇建，李玉龙，陈颖，等.炸药条加载圆柱壳的数值模拟（Ⅰ）：流固耦合模拟［J］.高压物理学报，2012，26（2）：155－162.Mao Yongjian，Li Yulong，Chen Ying，et al.Numerical simulation of cylindrical shell loaded by explosive rods（Ⅰ）：Fluid－structure interaction simulation［J］.Chinese Journal of High Pressure Physics，2012，26（02）：155－162.

［12］毛勇建，李玉龙，陈颖，等.炸药条加载圆柱壳的数值模拟（Ⅱ）：解耦分析与实验验证［J］.高压物理学报，2013，27（1）：76－82.Mao Yongjian，Li Yulong，Chen Ying，et al.Numerical simulation of cylindrical shell loaded by explosive rods（Ⅱ）：Decoupling analysis and experimental validation［J］.Chinese Journal of High Pressure Physics，2013，27（1）：76－82.

［13］毛勇建，李玉龙，陈颖，等.炸药条加载圆柱壳的数值模拟（Ⅲ）：对X射线力学效应的模拟等效性分析［J］.高压物理学报，2013，27（5）：711－718.Mao Yongjian，Li Yulong，Chen Ying，et al.Numerical simulation of cylindrical shell loaded by explosive rods（Ⅲ）：Fidelity for simulating X－ray mechanical effects［J］.Chinese Journal of High Pressure Physics，2013，27（5）：711－718.

［14］赵国民，王占江，张若棋.用柔爆索构成沿圆柱壳体周向呈余弦分布的冲量载荷［J］.爆炸与冲击，2008，28（6）：557－560.Zhao Guomin，Wang Zhanjiang，Zhang Ruoqi.To form a cosine distribution impulse around cylindrical shell circumference by using mild detonating fuse［J］.Explosion and Shock Waves，2008，28（6）：557－560.

［15］岳晓红，毛勇建，何荣建，等.片状炸药的比冲量标定技术：火炸药技术及钝感弹药学术研讨会［C］∥火炸药技术及钝感弹药学术研讨会.2002：396－398.

［16］林鹏，王长利，王等旺.挠性炸药比冲量的数值模拟与实验研究［J］.火炸药学报，2011，34（4）：30－33.Lin Peng，Wang Changli，Wang Dengwang.Numerical simulation and experimental studies on impulse of flexible explosive［J］.Chinese Journal of Explosives and Propellants，2011，34（4）：30－33.

［17］郭志昀，王占江，卢强，等.柔爆索引爆薄片炸药的比冲量研究［J］.兵工学报，2013，34（增刊1）：182－186.Guo Zhiyun，Wang Zhanjiang，Lu Qiang，et al.Research on specific impulse of the sheet explosive ignited by mild detonating fuses［J］.Acta Armamentarii，2013，34（suppl 1）：182－186.

A computational model for impulse coupling between sheet explosive and target

Lu Qiang，Wang Zhanjiang，Liu Xiaoxin，Guo Zhiyun，Wu Yujiao
（Northwest Institute of Nuclear Technology，Xi’an 710024，Shaanxi，China）

The sheet explosive can be used to simulate the space structure response caused by the highpower pulse X－rays，and the impulse coupling of the sheet explosive and the target is the basis for designing the simulated load.Based on the numerical results by the nonlinear finite element code，the computational modeling for the impulse coupling of the sheet explosive and the target is formulated in consideration of the effect on the specific impulse of the sheet explosive caused by the rarefaction of the border of the sheet explosive and the reflection of the support for connecting the mild detonating fuse and the sheet explosive.The analytic results reveal that the increment of the specific impulse caused by the rarefaction of the border is approximately in inverse relation to the diameter of the sheet explosive，and that caused by the reflection of the support is approximately in inverse relation to the square of the diameter of the sheet explosive.The specific impulse for the sheet explosive converges to the limit specific impulse related to the depth of the sheet explosive as the diameter of the sheet explosive reaches infinity.Both the rarefaction for the border of the sheet explosive and the reflection of the support are negligible with the diameter of the sheet explosive increasing.There exists a critical diameter and when it is equaled by the diameter of the sheet explosive，the specific impulse for the sheet explosive equals the limit specific impulse as the diameter of the sheet explosive reaches infinity.

mechanics of explosion；impulse coupling；specific impulse；sheet explosive

O383国标学科代码：13035

A

10.11883／1001－1455（2017）01－0084－08

（责任编辑 王易难）

2015－09－10；

2016－01－18

卢 强（1984— ），男，博士研究生；通信作者：王占江，wangzhanjiang＠nint.ac.cn。