无控子弹侵彻机场跑道数值仿真*
2011-12-07汪文革王鹏华
朱 剑,汪文革,王鹏华
(1 91428部队,浙江宁波 315000;2解放军炮兵学院,合肥 230031)
0 引言
现代战争中,使用战术导弹毁伤敌机场跑道可以有效的遏制敌空军力量的发挥。为了提高毁伤能力,战术导弹大多装载侵彻子母弹,通过高空抛撒大量子弹对机场跑道先侵彻后爆炸,以增强对混凝土跑道的毁伤效果。目前对该问题的研究,主要是进行靶场试验,但耗资巨大,效费比不高。文中对战术导弹无控子弹侵彻机场跑道进行了数值仿真研究,并对仿真结果进行了分析。
1 机场跑道有限元简化模型
针对文中所要研究的问题,结合典型机场跑道实际结构和尺寸大小,建立了混凝土层、砂石层和粘土层三层复合靶跑道模型,如图1所示。
弹体对机场跑道的侵彻是一个多种物质相互接触作用、大范围靶体单元中局部物质迅速变形失效的过程,在有限元计算中用Lagrange方法即可准确模拟。由于受计算机处理能力的限制,同时根据结构的对称性并考虑计算周期,只能通过建立子弹侵彻通道周围适当范围的半无限1/2跑道模型来模拟大范围机场跑道,并将四周和最下层底面设为透射边界,避免应力波反射。采用变网格结构对跑道模型进行映射网格划分,使侵彻通道周围网格加密,如图2所示。图3是子弹有限元网格模型。考虑到文中只研究侵彻问题,便简化掉子弹内部爆炸部分,同时对子弹进行质量补偿。

图1 典型机场跑道模型
2 材料模型和参数
假设计算所用子弹为钢质杆弹,材料取为线性硬化体,其静水压力 pd与体积变形之间用如下的Gruneisen状态方程描述,即:


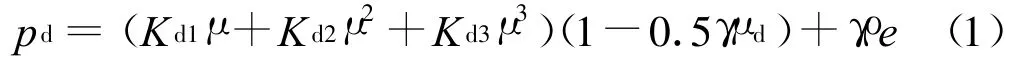
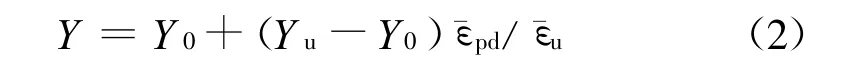
式中:Y0为初始屈服应力;Yu为极限屈服应力;ˉεpd为子弹等效塑性应变为子弹极限等效塑性应变。
混凝土是一种多孔脆性材料,自然状态下含有大量的微小孔隙和裂隙。根据混凝土材料的破坏特点,假定材料的损伤完全是由塑性流动变形引起的,则损伤演化方程可表示为:

砂石层是由大小相似的碎石碾压而成,其特点是抗压性好而抗拉性差、易碎。根据砂石层的性质,采用HJC模型能较好地反映砂石层在动力学条件下的状态特性。HJC模型是专门针对脆性材料在冲击载荷作用下而开发的动态模型,模型考虑了大应变、高应变率和高压情况,同时结合损伤理论考虑了材料的拉伸脆断,针对一种有空隙的材料,还考虑了材料压溃后的体积压缩量与压力的函数关系。在HJC模型中材料屈服面定义为:
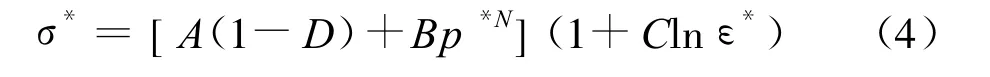
式中:A、B、N分别为无量纲粘性常数、压力强化系数和压力硬化指数;C为应变率系数,ε*为无量纲应变率,定义为实际应变率与参考应变率的比值;σ*为无量纲等效应变力;p*为无量纲压力;D为损伤度。该模型部分参数的具体确定方法可见文献[3]。
压实粘土层选用粘土和泡沫塑料模型Soil-and-Foam,能较好地反映压实粘土受子弹侵彻作用时的响应过程。
综上所述,文中仿真计算采用的材料模型相关参数见表1。
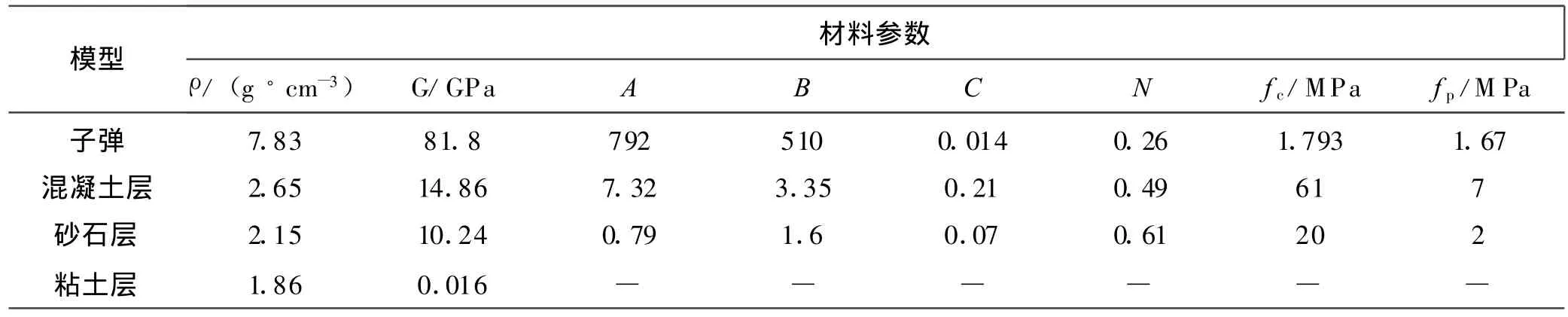
表1 材料模型参数
3 子弹侵彻机场跑道的姿态分析
文中研究的子弹为无控子母弹,在母弹解爆抛撒子弹到落地这段时间内,子弹会受到风力作用,子弹轴线与子弹速度方向之间会产生夹角即攻角,从而使子弹的落地姿态发生变化。
如图4,以机场跑道平面为XOZ平面建立空间坐标系OXYZ。子弹落地速度为V,O′为子弹重心,A为子弹落地速度方向线与跑道平面的交点,B为子弹头部顶点在跑道平面的映射点,A′为子弹重心在跑道平面的映射点,l为跑道平面的法线,l′为子弹轴线。则子弹落地速度方向与跑道平面法线l的夹角为入射角α,子弹轴线 l′与子弹速度方向的夹角为攻角 β,线段BA′与X轴的夹角为侧滑角γ。侧滑角γ是因旋转弹丸有攻角β时存在偏航产生的。显然,入射角α、攻角β共同决定了子弹侵彻机场跑道的姿态。经过分析可得子弹侵彻机场跑道的姿态分类如下式所示:
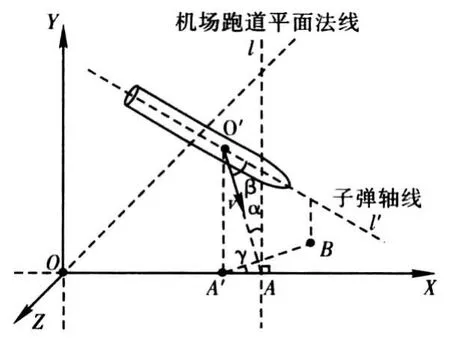
图4 子弹落地姿态示意图

4 仿真计算结果及讨论
4.1 结果演示
在建立了有限元模型的基础上,分别对子弹侵彻机场跑道的三种姿态进行了仿真计算。下面是各种姿态的演示算例。
图5为子弹以700m/s的初始速度垂直侵彻机场跑道的物理图像。图5(a)为子弹最初侵彻混凝土层的过程,可看到子弹头部由于高速冲击出现挤压变形,混凝土层初步开坑;图5(b)为子弹侵彻至混凝土层和砂石层结合部,头部持续受力导致变形加剧,混凝土层成坑加深,并开始形成空腔,同时由于冲击,砂石层结构开始松动;图5(c)为子弹进一步侵彻砂石层,两层材料界面崩裂并向四周扩张,同时空腔也向四周膨胀;图5(d)为混凝土空腔进一步膨胀,子弹侵彻到砂石层和土壤层结合部,并开始进入土壤层,砂石、土壤交界面也发生崩裂。由于塑性土壤材料较松软,子弹速度已较小,至此子弹头部变形已基本停止;图5(e)、图5(f)为子弹继续侵彻土壤层,侵彻深度稳定增加。由于高速冲击的后效性导致混凝土层空腔继续膨胀,但膨胀程度已比较有限。材料交界面崩裂继续扩张至停止。

图5 子弹正侵彻机场跑道的物理图像
图6 为子弹以入射角15°、初始速度800m/s侵彻机场跑道的物理图像。图6(a)、图6(b)为子弹侵彻机场跑道混凝土层过程;图6(c)、图6(d)为子弹侵彻砂石层过程;图6(e)、图6(f)为子弹侵彻土壤层过程。与垂直侵彻情况相比,斜侵彻的开坑更加明显,弹坑孔径大,大约是垂直侵彻的2到3倍,对跑道有更大的破坏范围。说明子弹对机场跑道斜侵彻效果较好,弹坑口径较大,混凝土层、砂石层都被穿透,弹道不发生偏转。

图6 入射角为15°时侵彻过程图
图 7 为子弹以攻角 30°、侧滑角 30°、入射角 30°、初始速度800m/s侵彻机场跑道的物理图像。可见,与没有攻角相比,子弹带攻角侵彻机场跑道弹坑非对称,这是由于子弹速度方向与轴线方向存在夹角,则受力方向与轴线方向也存在夹角,所以子弹侵彻跑道时总受到一个扭转力矩的影响,导致子弹侵彻路径发生扭曲,子弹尾翼迅速冲击跑道,改变了弹坑形态,同时子弹侵彻动能被迅速消耗。

图7 攻角、侧滑角都为30°的侵彻图像
4.2 分析讨论
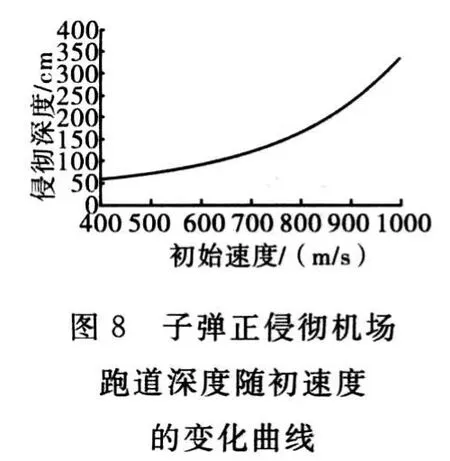
通过分析仿真试验数据可以得出子弹正侵彻机场跑道深度随初速度的变化曲线如图8所示。显然,随着初始速度等比例增大,子弹侵彻机场跑道的深度也随之增加,并且增加的幅度有变大的趋势。
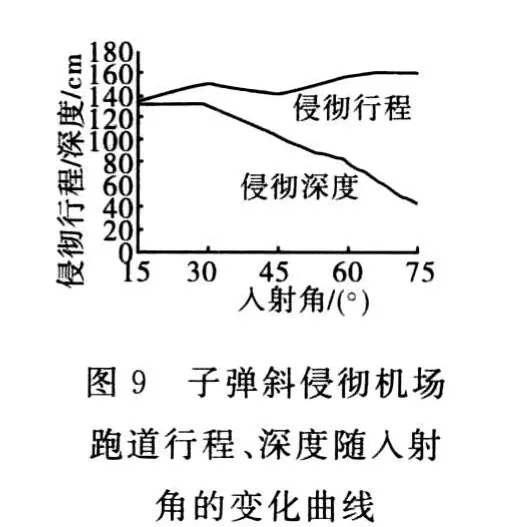
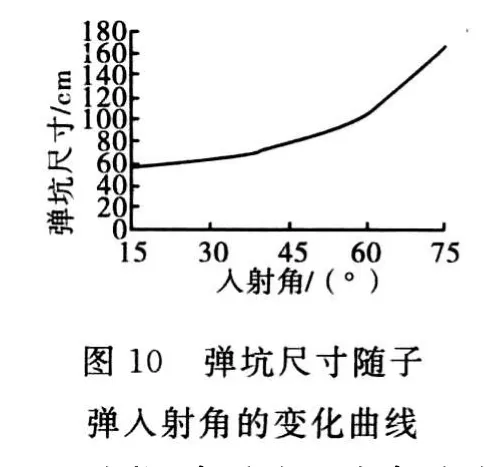
子弹斜侵彻机场跑道行程、深度随入射角的变化曲线如图9所示。可见,入射角等比例增大时,子弹对机场跑道的侵彻行程变化不大,而侵彻深度则显著减小,并且减小的幅度变大。弹坑尺寸随子弹入射角的变化曲线如图10所示。可见,入射角越大,弹坑尺寸越大,并且增大速度加快。这是由于入射角较小时,子弹以向下侵彻运动为主,而入射角较大时,则子弹在水平方向上运动的距离较大,导致弹坑扩张幅度变大。

侧滑角变化、攻角变化、攻角和侧滑角都变化时,子弹侵彻机场跑道深度随角度的变化曲线如图11所示。虚线表示侵彻深度随攻角的变化曲线,实线表示侵彻深度随侧滑角的变化曲线,虚线下行速度较快说明攻角比侧滑角更能影响子弹侵彻机场跑道的深度。显然,攻角和侧滑角都变化对侵彻深度影响的点划线曲线下行速度最快。同时,三种情况下侵彻深度的减小速度都在增大。这时可找到这样一个入射角:既能使子弹侵彻跑道深度较大,又能兼顾到跑道弹坑较大,这个点就是子弹的最佳入射角。
侵彻深度与弹坑尺寸随入射角的变化曲线如图12所示。实线表示侵彻跑道深度随入射角的变化曲线,虚线表示弹坑尺寸随子弹入射角的变化曲线,两者交于一点Q。点Q的横坐标大约为40°。所以该型子弹侵彻机场跑道的最佳入射角约为40°。
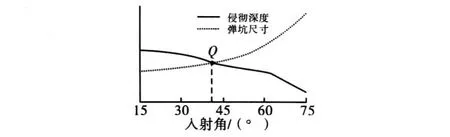
图12 子弹斜侵彻跑道深度和弹坑尺寸随入射角的变化曲线图
5 结束语
文中运用动力学仿真软件ANSYS/LS-DYNA对战术导弹无控子弹侵彻机场跑道进行了数值仿真研究,通过分析仿真结果发现:子弹落地速度大小、入射角、攻角和侧滑角四个因素影响子弹对机场跑道的侵彻效能;子弹以攻角姿态侵彻机场跑道所形成的弹坑呈现不规则形态,侵彻效果与正侵彻、斜侵彻有明显差异;存在最佳入射角,可使子弹侵彻机场跑道效能达到最大。
[1] 曾必强,姜春兰,李明,等.侵彻弹斜侵彻多层介质的三维数值仿真[J].弹道学报,2008,20(2):1-4.
[2] 马荷梅,张若京.弹丸侵彻混凝土土壤复合介质分析模型[J].力学季刊,2005,26(3):428-432.
[3] Forrestal M J,Frew D J,Hanchak SJ,et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].Int.J Impact Engng,1996,18(5):465—476.
[4] 宋顺成,谭多望,才鸿年.穿破甲有限元的几何非线性及物理参数的确定[J].爆炸与冲击,2002,22(2):137-143.
[5] Dancygier A N,Yankelevsky D Z.High strength concrete response to hard projectile impact[J].Int.J Impact Engng,1996,18(6):583-599.
[6] 王峰,胡秀章,王肖钧,等.卵形杆弹侵彻混凝土靶的有限元数值模拟[J].弹道学报,2008,20(2):9-12.
