借助几何画板推广Morgan定理

●

(宁波教育学院 浙江宁波 315010)

借助几何画板推广Morgan定理

●陈咸存

(宁波教育学院 浙江宁波 315010)

0 引言

关于三角形内某一图形面积与原三角形面积的比值问题已引起很多人的关注，如文献[1]得到：

美国的9年级学生Morgan利用几何画板推广了上述结论，得到Morgan定理.后来，在教师的指导下证明了这一结论，并于1994年5月受邀在美国Towson State University的数学研讨会上作了报告，他的年龄引起了与会者的极大关注[2].

图1

图2

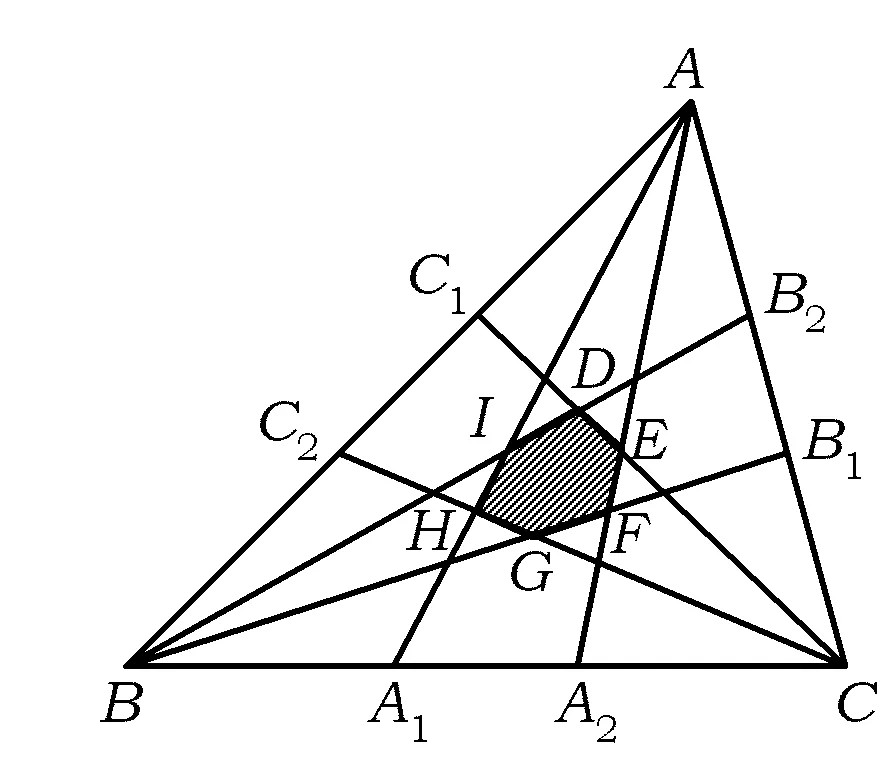
图3

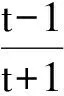
1 猜想

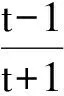
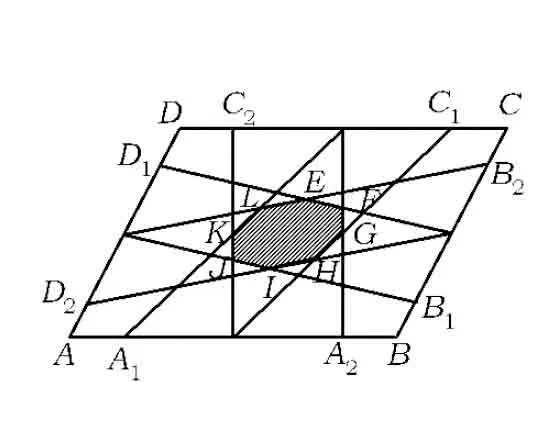
图4

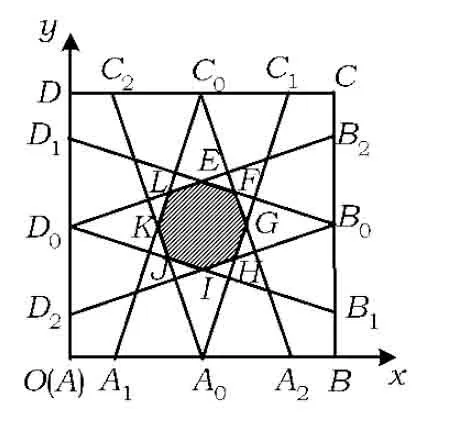
图5

表1 参数t对应的值

由表1知

解得

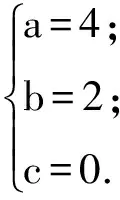
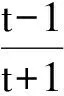
2 证明

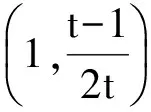
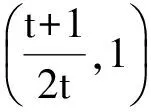
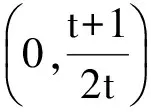
可求得

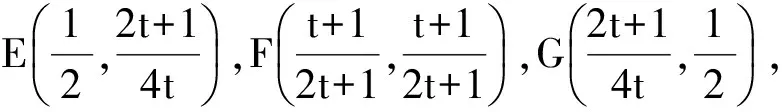
从而

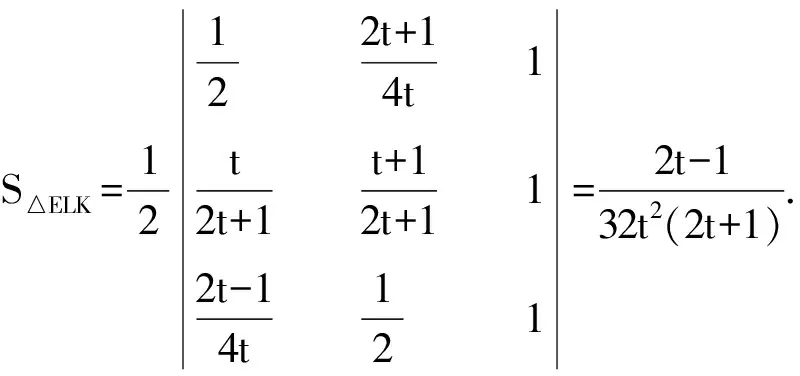
类似可得

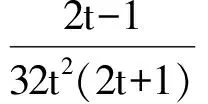
同理可得

类似可得

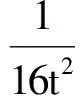
从而

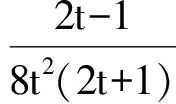
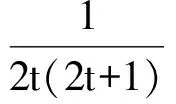
而SABCD=1，故

由两图形面积之比是仿射不变量知猜想成立.

3 结论

人们对数学研究方法的描绘往往集中于利用纸、笔进行运算和证明，很难体会观察、实验、尝试、猜测等活动对数学的作用，其实这些也是数学研究的重要方式.计算机及数学软件的发展，为数学研究提供了检验猜想的工具，使数学研究方式发生了变化.在这个“做数学”的过程中，不仅有计算或演绎，而且涉及观察、猜测、尝试、调控、估计、检验等多种方式，让学生感受、体会这些数学研究的基本方法将使他们终生受益[5].

[1]Cuoco A,Goldenberg P,Mark J.Reader Reflections:Marion′s theorem[J].Mathematics Teacher,1993,8(86):619.

[2]Watanabe,Tad,Hanson R,Nowosielski F D.Reader Reflections:Morgan′s theorem[J].Mathematics Teacher,1996,5(89):420-423.

[3] 陈咸存.Morgan定理的推广[J].数学通报,2000(2):44-46.

[4] 朱德祥.高等几何[M].北京：高等教育出版社，2000.

[5] 刘兼，孙晓天.数学课程标准解读[M].北京：北京师范大学出版社，2002.