以美启真巧解题
2011-11-28
●
(桂林师范高等专科学校数学与计算机科学系 广西桂林 541002)
以美启真巧解题
●罗奇
(桂林师范高等专科学校数学与计算机科学系 广西桂林 541002)
美是客观世界的一种自然属性,数学作为描述客观世界的工具当然也具有美的属性.正如英国数学家罗素(Russell,1872-1970年)所说“数学,如果正确地看,不但拥有真理,而且具有至高的美”.数学美的内容是多方面的,总的来说,数学美的表现常具有简洁与秩序、对称与平衡、统一与协调、奇异与极端等特征.并且数学美的这4个方面内容相互联系、相互渗透,它们构成了和谐与奇妙的数学世界.
数学美在数学解题中具有逻辑思维无法代替的作用,它统领着解题的思想方法,启迪着解题的直觉思维,往往能够引领我们找到解题的方向和途径,那么如何利用数学美来指导解题呢?这就要求我们在分析和处理问题时有意识地用数学美的特征去考察和感悟数学对象,思考和转化数学问题,进而培养对数学的美感.下面通过几个例题来欣赏如何利用数学美指导解题.
1 以简驭繁、变乱为序,追求简洁与秩序美
简洁、清晰、秩序、明快,会给人以美感.数学以高度抽象、极其简洁的形式和思想反映客观世界.在杂乱无章的客观现象中,抽象出秩序井然的数学理论,又用简单、有序的数学形式来表达、解释并处理更多的客观事物和现象,这就是数学的简洁与秩序美.
许多的数学问题,虽然其表现形式可能较为复杂和无序,但其本质总是存在简单和秩序的一面.这就要求我们在处理问题时尽可能用简洁与秩序的观点和方法对数学问题进行转化,从问题的各个方面选择新信息,并有效地对已知信息进行组合、编码以获得最佳解题方案.譬如利用未知、已知换位处理,往往能够化难为易.
例1已知a∈[0,1],解关于x的不等式:
(a-1)lg2x-9algx+2a+1>0.
分析一般地,将不等式看成是关于lgx的二次不等式,利用换元法求解,但整个过程较繁杂.注意到在不等式中a的最高次数是1,相对x更为简单.若把x作为已知,把a作为变量,则可将原不等式化为关于a的一元一次不等式,并按a的降幂顺序排列得
f(a)=(lg2x-9lgx+2)a-lg2x+1>0,
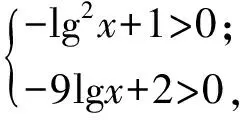
化简得

即

同样利用变换、构造、排序等转化的策略,也能够获得解题的突破口.
例2求由1,2,3,…,n这n个数组成的允许重复的m个数的数组的组数.
分析在1,2,3,…,n中任取一个允许重复的m个数组成的数组集合为
A={(a1,a2,…,am)|1≤a1,a2,…,am≤n},
所求的组数就是集合A的元素个数.从简洁与秩序美的观点考虑,将A中的数组从小到大排序,得到集合B={(b1,b2,…,bm)|1≤b1≤b2≤…≤bm≤n,bj=ai(1≤i≤m,1≤j≤m)},集合B的元素仍然是有重复数的数组.为了更为简洁,构造一个没有重复数的数组集合C,使从集合B到集合C之间建立一个双射f,为此将b1,b2,…,bm从第1个开始分别加上0,1,2,…,m-1得到m个数c1,c2,…,cm,这样得到集合
C={(c1,c2,…,cm)|1≤c1 德国数学家魏尔斯特拉斯指出“美和对称性紧密相连”.数学中的对称与平衡美不单指形象的几何图形对称,也包括抽象的关系、地位、形式、方法等的对称与平衡. 对称与平衡美是数学美的重要特征之一,在数学解题中,我们应充分利用数学知识、方法、形式或图形的对称与平衡性求解.一方面,具有相同结构特征的数式具有同等的地位和相同的处理手法,另一方面,数式结构的对称也蕴含着解法的对称. 例3已知四面体V-ABC的6条棱长之和为l,且∠AVB=∠BVC=∠CVA=90°,求它体积的最大值. 分析设VA=a,VB=b,VC=c,则 因此 (1) 而V-ABC的体积为 (2) 于是问题转化为在式(1)的条件下,求式(2)的最大值.观察式(1)和式(2)知,a,b,c地位对等,可以从对称与平衡的原则出发,提出猜想:由对称性,是否当a=b=c时体积最大呢?此时 从而 因此只要证明 即证 而上式是成立的,因为 对偶关系也可视为对称与平衡的一种形式.在解题中,如何“配对”以及应“配”些什么,都应在对称与平衡美的引导下进行. 分析注意到 将上述两配对式相乘得 因为 72n+1=7(50-1)n=7[5p+(-1)n]= 35p+7(-1)n= 35q+2(-1)n(p,q∈Z), 数学作为研究客观世界的数量关系和空间形式的科学,它反映了客观世界的统一与和谐.数学的统一与和谐美是指数学各分支之间、分支内部及分支与整体之间互相贯通、和谐和互相转化. 统一与和谐美也是促使解题成功的重要因素之一,数学除了在形式上追求统一与和谐之外,在结论、方法上也追求统一与和谐. 可见利用圆锥曲线的统一方程,不仅很容易地证明了结论,而且还推广了结论! 我们也常常通过变换已知与未知的数、式、形,使它们消除差异而达到统一与和谐的形式来启迪解题思路、发现解题规律. sinB<3(sinC-sinA), 这样就实现了与已知条件相对统一和谐.但还不够,不等式中有3个角,能否把它们化为同角的三角函数呢?考虑到3A+B=π,则C=2A,于是 sin3A<3(sin2A-sinA). 再把倍角统一成单角,得 3sinA-4sin3A<3(2sinAcosA-sinA), 由sinA>0得 3-4sin2A<3(2cosA-1), 再把不同名的三角函数统一为同名的三角函数, 2cos2A-3cosA+1<0, 即 (2cosA-1)(cosA-1)<0. 奇异与极端也是一种美,正如英国哲学家培根所说“没有一个极美的东西不是在调和中有着某些奇异”,我国著名数学家徐利治教授也指出“奇异是一种美,奇异到极度更是一种美”.数学的奇异与极端美,是指数学中的统一与和谐或对称与平衡在一定条件下的破坏,是数学中的新思想、新理论、新方法对原有的习惯法则和格局的突破. 一些出人意料的想法往往是极端的设想,但常能使问题豁然开朗.譬如运用特殊化方法探讨几何图形的极端位置,就体现了数学的奇异与极端美. 例7一圆与直线3x+4y+5=0相切于点(1,-2),且经过点(4,7),求圆的方程. 分析切点(1,-2)可以看成半径为0的圆,直线3x+4y+5=0可看成通过该圆的直线,基于这种奇异和极端的想法,此题可以跳出设圆方程的一般方法,用曲线系方程来求解,则更为简捷. 首先过切点(1,-2)的方程为(x-1)2+(y+2)2=0,通过直线3x+4y+5=0和该点圆的圆系方程为 (x-1)2+(y+2)2+t(2x+4y+5)=0, 代入点(4,7)的坐标,求得t=-2,故所求圆的方程为 (x-1)2+(y+2)2-2(3x+4y+5)=0, 即 x2+y2-8x-4y-5=0. 对于某些数学问题,若能抓住其“个性特点”,打破问题求解的习惯法则,寻找它与其他知识的联系,则往往能找到出人意料的新奇解法和出人意料的结果. 分析本题若利用三角公式进行化简求值,需要利用和差化积和倍角公式以及恒等变形的化简技巧,过程比较复杂.那么是否可以利用所给式子是余弦函数的代数和以及余弦函数积化和差后仍然是余弦函数的代数和的个性特点求解? 解得 同样地,借助统一与和谐美的思想将原式的运算符号统一,可以得到: 联想复数与三角之间的关系,可将三角问题化归为复数问题求解.如果观察到各个角度的倍数关系,那么还可以构造几何图形或者向量求解……如此新奇的解法无不体现了数学知识的和谐与奇异. 可见数学问题的求解需要数学美的引领,并且也应该以美启真去追求那些漂亮的解法,这样在我们心灵深处就会引起一种愉快的体会和欣赏.通过如此长期的训练,我们就能透过抽象的数学符号看到美的形象,透过严密的逻辑推演领略美的神韵,就可以完善人的思维品质、陶冶人的情趣、增强人的创造能力.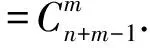
2 左右均衡、前后照应,联想对称与平衡美

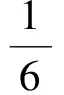
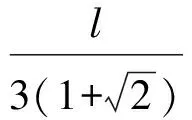
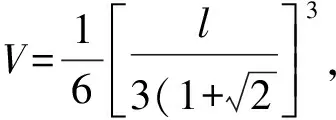
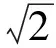



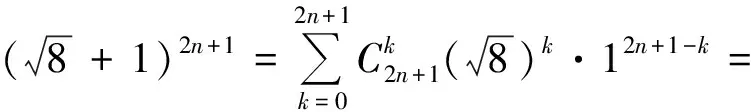
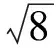

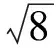
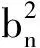
3 化分歧为一致、变混乱为协调,利用统一与和谐美
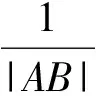


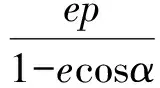
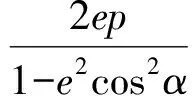
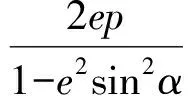

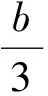
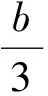

4 标新立异、探讨极致,揭秘奇异与极端美