Dirichlet型空间到μ-Bloch空间的加权Ces‘aro算子

赵艳辉, 张学军

(1.湖南科技学院数学与计算科学系,湖南永州 425006; 2.湖南师范大学数学与计算机科学学院,湖南长沙 410006)

Dirichlet型空间到μ-Bloch空间的加权Ces‘aro算子

赵艳辉1, 张学军2

(1.湖南科技学院数学与计算科学系,湖南永州 425006; 2.湖南师范大学数学与计算机科学学院,湖南长沙 410006)

主要讨论了Cn中单位球上Dirichlet型空间Dp到μ-Bloch空间βμ的加权Ces‘aro算子Tg的有界性和紧性问题,给出了Tg为Dp到βμ有界算子或紧算子的充要条件.

Dirichlet型空间,μ-Bloch空间;加权Ces‘aro算子;有界性;紧性

1 问题的引进和定义

用dv表示Cn中单位球B上的正规Lebesgue测度,dσ为单位球面δB上的正规面测度.设B表示Cn上的单位球,H(B)代表B上的全纯数类.对[0,1)上的连续函数μ(r)=0,如果存在常数a,b (0＜a＜b),使得

则称μ是[0,1)上的一个正规函数.作为一个加权,正规函数μ通常被用来定义混合模空间[1].设μ是一个正规函数,B上的全纯函数f如果满足

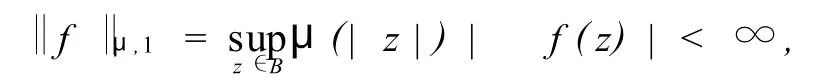
则称f属于μ-Bloch空间βμ;如果f满足

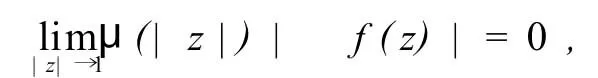
[2]可知,存在常数c＞0,使得

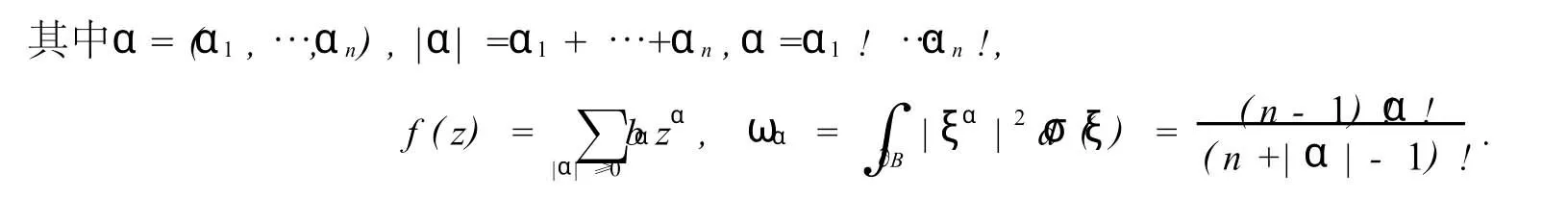
我们知道,D0为Hardy空间H2,D-1为Bergman空间L.

在单复变中定义了如下Ces‘aro算子:

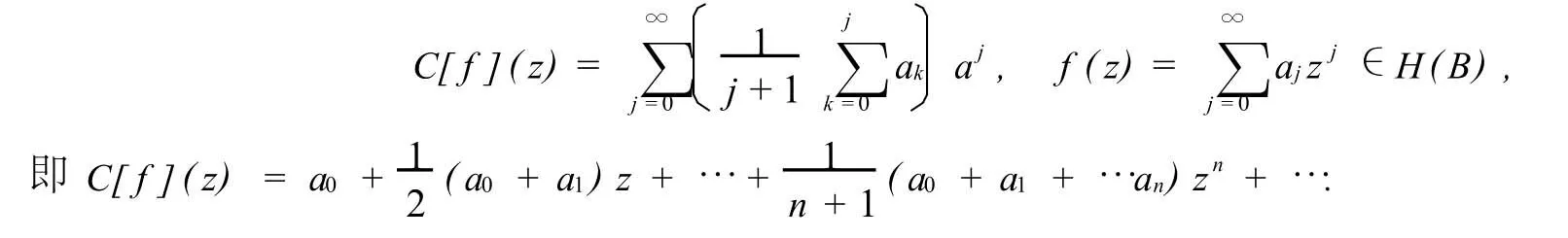
对多复变的情形,给定g∈H(B),定义加权Ces‘aro算子为

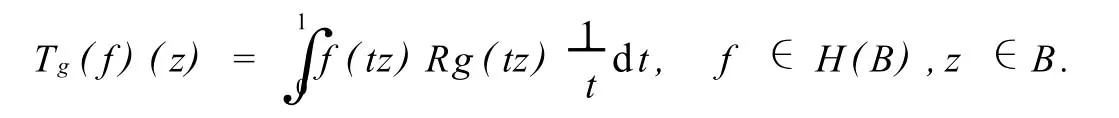
文献[1],[10]在单位球中讨论了混合模空间和Bloch型空间上加权Ces‘aro算子的有界性和紧性问题.文献[11]讨论了单位球中Bloch型空间βp之间及Dirichlet型空间Dq之间的加权Ces‘aro算子的有界性和紧性问题.本文的主要工作就是在Cn中的单位球上来给出Tg为Dirichlet型空间Dq到βμ空间的有界算子和紧算子的充要条件.

2 有关引理及其证明

引理2.1[14]若f∈Dp,则

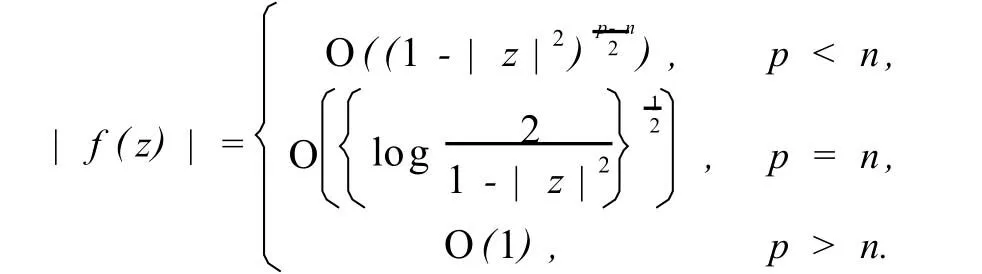
引理2.2 设μ为[0,1)上的正规函数,g∈H(B),则Tg为Dp到βμ的紧算子的充要条件是:对Dp上任一有界序列{fj},如果它在B的任一紧子集上一致收敛于0,就有‖Tg(fj)‖βμ→0(j→∞).

证由引理2.1和Montel定理按定义可证.

3 关于加权Ces‘aro算子的有界性

定理3.1 设-∞＜p＜+∞,μ为[0,1)上的正规函数,g∈H(B),则Tg为Dp到βμ之有界算子的充要条件是:

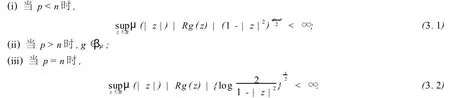
证(i)充分性.任取f∈Dp,由于Tg(f)(0)=0,且R[Tg(f)](z)=f(z)Rg(z),由引理2.1可得

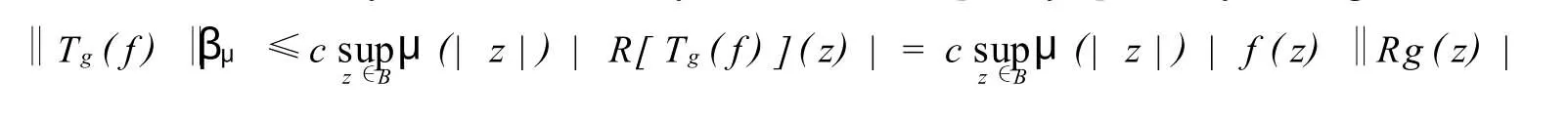
这表明Tg是Dp到βμ的有界算子.

必要性.设Tg为Dp到βμ的有界算子,当p＞n时,取f(z)=1,因为

所以‖fω‖Dp≤c.由Tg是Dp到βμ的有界算子知

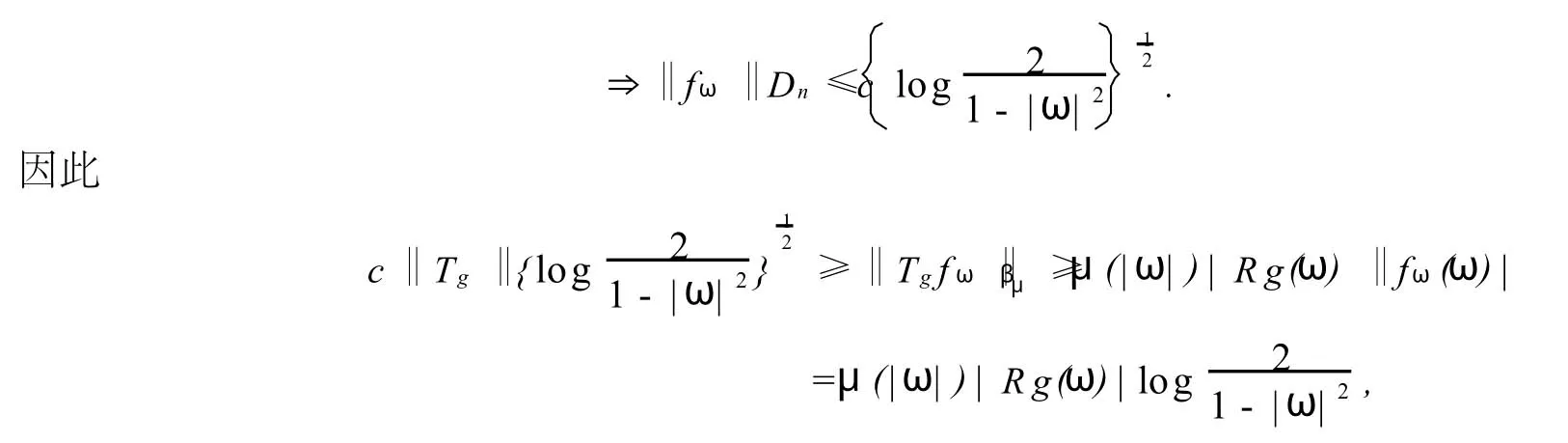
由ω的任意性知当p=n时,(3.2)式成立.

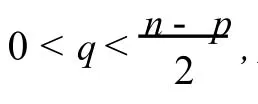
证此时由定理3.1知

再由极大模原理有Rg(z)=0,这意味着g为常值函数.

4 关于加权Ces‘aro算子的紧性

定理4.1 设-∞＜p＜+∞,μ为[0,1)上的正规函数,g∈H(B),则Tg为Dp到βμ之紧算子的充要条件为

证(i)充分性.若(i),(ii),(iii)成立,则g∈βμ.任取点列{fj},满足‖fj‖Dp≤1且在B上内闭一致收敛于0.

当p＜n时,若(4.1)式成立,则对∀ε＞0,存在0＜δ＜1,当δ＜|z|＜1时,有

由于{fj}在E={z∶|z|≤δ}上一致收敛于0,故存在自然数N,当j＞N时,有|fj(z)|＜ε对一切z∈E成立.从而当j＞N时,由引理2.1及g∈βμ知

由ε的任意性和引理2.2知Tg为Dp到βμ的紧算子.类似可证:当p=n时,若(4.2)式成立时Tg为Dp到βμ的紧算子,当p＞n时,由g∈βμ,0类似可得结论.反之,设Tg为Dp到βμ的紧算子,取f(z)=1∈Dp可得g∈βμ.

下面证明(4.1)式成立.现假设(4.1)式不成立,则存在点列{zj}⊂B及常数ε0＞0,满足|zj|→1 (j→∞)以及

类似定理3.1中(i)的必要性的证明可得‖fj‖Dp≤c.且显然{fj}内闭一致收敛于0,根据引理2.2知

当p=n时,若(4.2)式不成立,则存在点列{zj}⊂B及常数ε0＞0,满足|zj|→1 (j→∞)以及

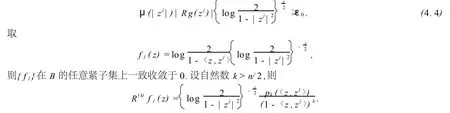
此处pk为至多k次的多项式,故由文献[12]中命题1.4.10可得

再由文献[13]中引理2.1知,‖fj‖Dn≤c.但由(4.4)式知

这与引理2.2矛盾!因此必有(4.2)式成立.

当p＞n时,下面证明g∈βμ,0.

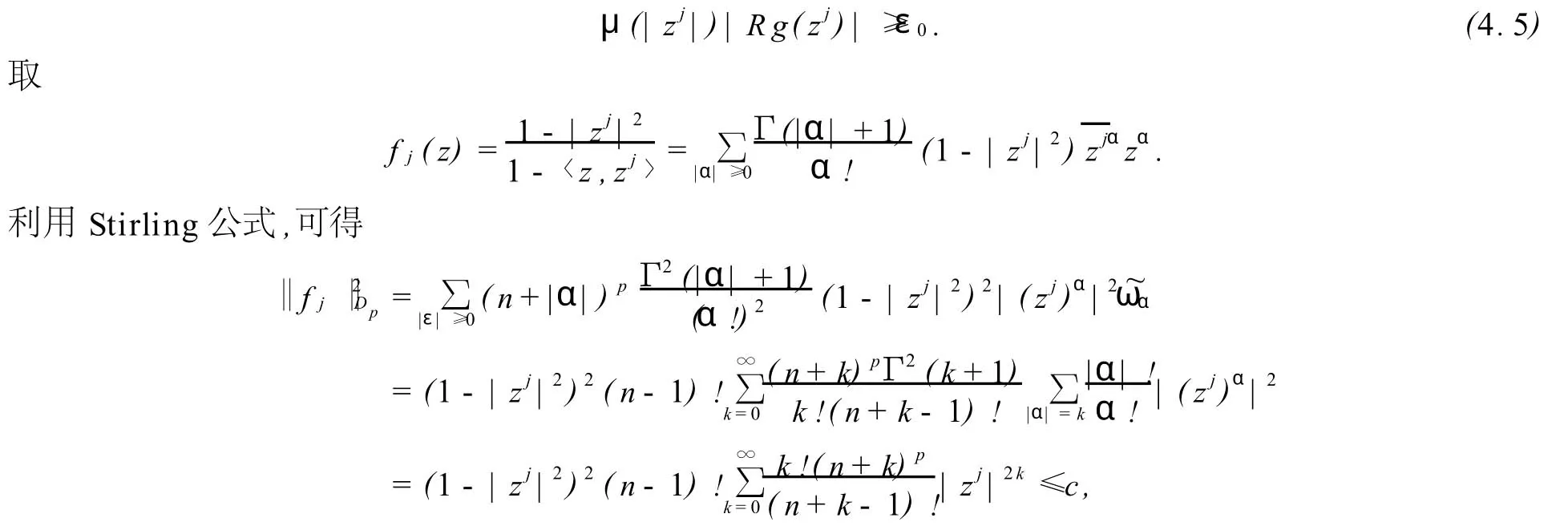
即{fj}在Dp上有界,且显然{fj}内闭一致收敛于0.根据引理2.2知

矛盾!因此必有g∈βμ,0成立.

[1] Hu Z J.Extended Ces‘aro operators on mixed norm space[J].Proc.Amer.Math.Soc.,2003,131(7)：2171-2179.

[2] Tang X M.Extended Ces‘aro operators between Bloch-type spaces in the unit ball ofCn[J].Math.Anal.Appl., 2007,326(2)：1199-1211.

[3] Miao J.The Ces‘aro operator is bounded onHpfor 0＜p＜1[J].Proc.Amer.Math.Soc.,1992,116：1077-1079.

[4] Shi J H,Ren G B.Boundedness of the Ces‘aro operator on mixed norm spaces[J].Proc.Amer.Math.Soc., 1998,126：3553-3560.

[5] Siskakis A G.Composition semigroups and the Ces‘aro operator onHp[J].J.London Math.Soc.,1987,36(2)：153-164.

[6] Xiao J.Ces‘aro operators on Hardy,BMOA and Bloch spaces[J].Arch Math.,1997,68：398-406.

[7] Xiao J,Tan H.p-Bergman spaces,α-Bloch spaces,littleα-Bloch spaces and Ces‘aro means[J].Chin.Ann.of Math.,1998,19：187-196.

[8] Aleman A,Siskakis A G.An integral operator onHp[J].Complex Variables,1995,28：149-158.

[9] Aleman A,Siskakis A G.Integration operators on Bergman spaces[J].Indiana University Math.J,1997,46：337-356.

[10] Hu,Z.J.Extended Ces‘aro operators on the Bloch space in the unit ball ofCn[J].Acta Math.Sci.,2003, 23B(4)：561-566.

[11] 张学军.Cn中Dirichlet型空间和Bloch型空间上的加权Ces‘aro算子[J].数学年刊,2005,26A(1)：139-150.

[12] Rudin W.Function theory in the unit ball ofCn[M].New York：Springer-Verlag,1980.

[13] 张学军.Cn中p-Bloch空间βp(B)和Dirichlet型空间Dq(B)之间的系数乘子[J].数学年刊,2003,24AC(1)：13-22.

Extended Ces‘aro Operator from Dirichlet Type Spaces toμ-Bloch Spaces on the Unit Ball

Z HAO Yan-hui1Z HA N G Xue-j un2
(1.Department of Mathematics and Computational Scienc,Hunan University of Science and Engineering, Yongzhou,Hunan 425006,China; 2.College of Mathematics and Computer Science,Hunan Normal University,Changsha 410006,China)

The necessary and sufficient conditions are given for the Extended Ces‘aro operatorTgto be bounded or compact from Dirichlet type spacesDptoμ-Bloch spacesβμon the unit ball ofCn.

Dirichlet type spaces;μ-Bloch spaces;extended Ces‘aro operator;boundedness;compactness

O174.56

A

1672-1454(2011)05-0056-06

2008-11-24;[修改日期]2009-05-31