关于定积分微元法的一点补充
2011-11-22佘智君
佘智君
(贵州大学理学院基础教学部,贵州贵阳 550003)
关于定积分微元法的一点补充
佘智君
(贵州大学理学院基础教学部,贵州贵阳 550003)
通过一个实例提出问题,进而给出微元法中推导微元及检验微元表达式的简便方法.[关键词]定积分;微元法;微分
1 引 言
《数学分析》和《高等数学》教材都介绍了微元法,应用微元法可将一些几何、物理等实际问题转化为定积分来求,而微元又是微元法的关键,能否合理选择所求量的微元,关系到所求量的正确性,那么究竟如何选择微元才能保证所取微元是合理的呢?学生经常感到困惑,以致于他们只能模仿例题“机械地套用”微元法.在“微元法”中,我们经常用直线段代替曲线段,以不变量代替变量,以均匀代替不均匀,那么是否直观上近似的量都可以作为所求量的微元呢?我们先看下面的例子.
设曲线y=f(x)>0是[a,b]上的光滑曲线,求该曲线绕x轴旋转一周所得旋转曲面的面积.
在直观上看,当d x→0时,在[x,x+d x]上切线段AB≈弧,直线段≈弧,那么切线段及直线段分别绕x轴旋转一周所得小扁圆台的侧面积是否都可以作为所求旋转曲面面积的微元d A呢?现记切线段=d s,直线段=d x.
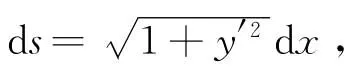

图1
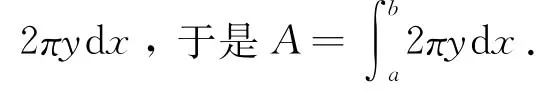
同一旋转曲面的面积,怎么会出现两个不同结果呢?这其中之一一定有误,问题又出在哪呢?
2 微元法的条件及证明
2.1 一般地,若所求量U满足下列条件:
(i)U是与某个变量x的变化区间[a,b]有关的量;
(ii)U对区间[a,b]具有可加性;
(iii)将区间[a,b]分成若干小区间,取其中任一小区间[x,x+d x],如果对应于区间[x,x+d x]的部分量ΔU能近似地表示为[a,b]上的一个连续函数在x处的函数值f(x)与d x的乘积,且ΔU=f(x)d x+o(d x),称f(x)d x为量U的微元,记作:d U,即d U=f(x)d x,则U=f(x)d x.上述方法称为定积分的微元法.
这时我们会提出以下问题:
2.2 为什么ΔU=f(x)d x+o(d x)就有U=f(x)d x?
关于该问题,《数学分析》和《高等数学》教材都没有作理论的论证,对此本文将作如下推导:
记U(x)=U[a,x],显然U(a)=0,U[a,b]=U.
因为ΔU=f(x)d x+o(d x),所以由微分的定义有d U=f(x)d x,于是U′(x)=f(x),再由牛顿-莱布尼茨定理得

2.3 如何检验ΔU=f(x)d x+o(d x)?
因为f(x)是要求的连续函数,也就是说U是未知的,所以要严格检验ΔU=f(x)d x+o(d x)是非常困难的,对此给出如下命题:
命题 设f(x)在[a,b]上连续,U是一个与区间[a,b]有关的量,且U对区间[a,b]具有可加性,若对区间[a,b]上的任意小区间[x,x+d x]有

其中M,m分别是f(x)在区间[x,x+d x]的最大、最小值,则

该命题的(*)式在许多实际问题中是可直观看出的,这样它不仅给出了如何求微元中的连续函数f(x),而且还克服了ΔU=f(x)d x+o(d x)不可直接检验的问题.
3 总 结


因此第二种解法是错误的,错误的根源在于忽略了微元的条件ΔU=f(x)d x+o(d x),误认为只要是所求量的近似量就可作为它的微元,所以应用微元法解决实际问题时,要特别注意其条件ΔU=f(x)d x+o(d x),在教学中应强调微元法的关键是根据实际问题确定被积函数f(x),从而正确的写出所求量的微元,把教学生如何找所求量的微元作为重点.
[1] 同济大学数学教研室.高等数学(上册)[M].4版.北京:高等教育出版社,2000.
[2] 陈传璋,金福临,朱学炎,欧阳光中.数学分析(上册)[M].2版.北京:高等教育出版社,1995.
[3] 陈玉,贺秋林.微元法原理探究[J].工科数学,2001,17(3):95-96.
A Supplement on Differential Element Method of Definite Integral
SHE Zhi-jun
(Department of Basic Sciences,Guizhou University,Guiyang,550003,China)
A question is proposed by aconcrete example,and we propose simple method for the deriving and detection of the differential expression.
definite integral;method of differential element;differential
O172
C
1672-1454(2011)04-0176-03
2008-09-26
