由有理数Cauchy列定义的实数的无限十进小数展开

陈同舟， 许 斌

（中国科学技术大学，合肥 230026）

由有理数Cauchy列定义的实数的无限十进小数展开

陈同舟， 许 斌

（中国科学技术大学，合肥 230026）

讨论了有理数Cauchy列定义的实数系的一种等价形式——无限十进小数展开，定义了其上的算术运算与顺序并证明了它们和已有的定义一致.

无限十进小数；实数系；算术运算

1 两个引理

以下约定两引理中RR都是有理数Cauchy列定义的实数系.

引理1.1 对所有固定正数h，∀x∈RR，x＞0，存在唯一的k∈ZZ，使（k-1）h≤x＜k h.

引理1.2 ∀x∈RR，x＞0，存在唯一的k∈ZZ，使10k-1≤x＜10k.

证因为｛m∈ZZ｜x＜10m｝是非空有下界集合，故其最小元k即是满足条件的唯一的k.

2 对由Cauchy列定义的实数x的无限十进小数展开

对由Cauchy列定义的正实数，由引理1.2，存在唯一的p∈ZZ，使10p≤x＜10p＋1.由引理1.1，存在唯一的ap∈ZZ，使得ap10p≤x＜ap10p＋10p，所以ap∈｛1，2，…，9｝.继续向下做，存在唯一的ap-1∈ZZ，使得

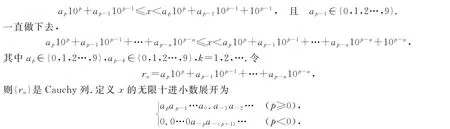
其中p＜0时，小数点后共有-（p-1）个0.若∃n∈NN，使任意的k＞n时，a-k＝0，则a-n后的那些0可以省略不写.

对负数，在-x前加一个负号.0对应0.000…，则可证不同的实数对应不同的展开.

3 对展开方式的补充以及另外一种展开方式

定理3.1 正实数x按照上面的方法可以表示成无限十进小数，且不会出现从某项ap-k起后面的ap-n都是9的情形.

证用反证法.若n＞k，有

则rk＋10p-k-10p-n≤x＜rk＋10p-k.对任意的n＞k，有rk＋10p-k-x≤10p-n，这不可能.

定理3.2 如果实数x，y，z满足y＜x＜z，且x1，x2，…是定义x的有理数Cauchy列，则存在m，使得对任意的k≥m，有y≤xk≤z.

对任一实数，可以定义它的另一种十进小数展开，下文所说的“新的展开方式”等等都是指这种展开方式.

因为任意x∈RR，存在n∈ZZ，使n≤x＜n＋1，故可记n为x的整数部分，x-n为x的小数部分，对x-n进行前面所定义的十进小数展开.

定理3.3 （i）若x非负或为负整数，则新的展开方式和原先的相同；

设x按原来方式展开形式如-n.x1x2…xk，按新方法展开形式如-m＋0.y1y2…yk，则断言m＝n＋1，且0.x1x2…xk＋0.y1y2…yk＝1.

证（i）显然.

（ii）因为由定义n＜-x＜n＋1，而-m＜x＜-m＋1，故m＝n＋1.显然此时

故0.x1x2…xk＋0.y1y2…yk＝1.

（iii）同上得m＝n＋1.下用归纳法证明对任意的i∈NN，有xi＋yi＝9.

1.i＝1时，存在x1，使得

2.若i＜k时成立，则i＝k时，存在惟一xk，使得

存在惟一yk，使得

故xk＋yk＝9.

这两种展开方法可以互相转换.

4 序关系

对任意的a＝（-）A0.a1a2…，b＝（-）B0.b1b2…∈，称a≤b当且仅当下面情况之一发生：

1.a的前面有负号而b的前面没有负号；

2.a，b的前面都没有负号，且A0＜B0；

3.a，b的前面都没有负号，且A0＝B0，存在k，使得i＜k时ai＝bi且ak＜bk；

4.a，b的前面都没有负号，且A0＝B0，任意的i，有ai＝bi；

5.a，b的前面都有负号，将a，b的负号去除掉后得到，有-b≤-a.易知

5 加 法

将a，b按新的方法展开，a＝A0＋0.a1a2a3…，b＝B0＋0.b1b2b3….

令Ak＝A0＋0.a1a2a3…ak，Bk定义类似.定义

由闭区间套原理可知，a＋b唯一存在.以下给出a＋b的无限十进小数展开：

1.设对任意的k，存在m≥k，任意的n≥m，使得An＋Bn与An＋Bn＋2×10-n的前k位小数都相同，则可确定a＋b的前k位小数，故可确定a＋b.

实际上，只要任意的k，存在m，使得Am＋Bm，Am＋Bm＋2×10-m的前k位小数相同即可.这是因为对任意的n≥m，

故Am＋Bm，Am＋Bm＋2×10-m的前k位小数相同，则当n≥m时，An＋Bn与An＋Bn＋2×10-n的前k位小数相同.故这两个陈述是等价的.

2.若1中的情况不成立，则存在k，使得对任意的m≥k，有Am＋Bm，Am＋Bm＋2×10-m的前k位小数至少有一个不相同.记

则对m＞k＋1，有两种情况：

1.C0＝D0且存在l，使得c1＝d1，…，cl-1＝dl-1，cl≠dl，显然l≤k.

2.C0≠D0.

对情况1，显然cl＜dl.若cl＋1≠dl，则cl＋2≤dl，故

因为l≤k＜m-1，故上式不可能成立，故只能cl＋1＝dl.

若cl＋1≠9，则cl＋1≤8，从而0.0…0cl＋1…cm＜9×10-l-1（小数点后有l个0）.于是

矛盾，故cl＋1＝9.依次这样做下去，可得cl＋1，…，cm-1都为9，故ck＋1，…，cm-1都为9.

若cm≤7，则0.0…0 9…9cm＜10-l-2×10-m（小数点后有l个0，m-l-1个9），

矛盾，故cm为8或9.

若cm＝8.显然这时Am＋1＋Bm＋1，Am＋1＋Bm＋1＋2×10-m-1的整数部分应相同.令Am＋1＋Bm＋1＝E0＋0.e1e2e3…em＋1，则

而em＝9，cm＝8，em＋1为8或9，所以am＋1＋bm＋1为1 8或1 9，只能am＋1＝bm＋1＝9，em＋1＝8.依次这样做下去，可知对任意的n，有am＋n＝bm＋n＝9，而这是被禁止的，故cm＝9.故存在m，k，使得n≥m时，An＋Bn的第k位小数往后都是9.

对情况2，讨论是类似的，同理可得存在m，k，使得n≥m时，An＋Bn的第k位小数往后都是9.则可令a＋b＝An＋Bn＋10-n.再将a＋b变为原来的表示形式即可.

由加法的定义，显然加法满足交换律.

定理5.1 加法满足结合律.

证将a，b，c按新的方法展开，

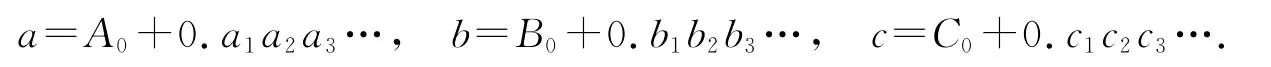
Ak，Bk，Ck定义同定义加法时的定义，Ak＋Bk≤a＋b＜Ak＋Bk＋2×10-k，故

由闭区间套原理可知（a＋b）＋c，a＋（b＋c）都唯一存在，且（a＋b）＋c＝a＋（b＋c）.

6 乘法，零元，负元，幺元，逆元

这样的实数系统有零元，有负元是显然的.

定义乘法前先需要定义实数的科学计数法表示，即对非零数a＝（-）apap-1…a0.a-1a-2…，则将a表示成（-）ap.ap-1…a0a-1a-2…×10-p.

下面定义乘法，只需考虑两正数相乘的情形，因为任何数和零相乘的积都定义为零.若a负b非负，令ab＝-（-a）b；若a非负b负，令ab＝-a（-b）；若a负b负，令ab＝（-a）（-b）.这三种情况均可化为a，b都非负的情形.

先考虑a＝a0.a-1a-2…，b＝b0.b-1b-2…的情况（其中a0，b0∈｛0，1，…，9｝），Ak＝A0.a1a2a3…ak，Bk定义类似.

由闭区间套原理可知，ab唯一存在，则用类似加法的方法可确定出ab.

对一般情况

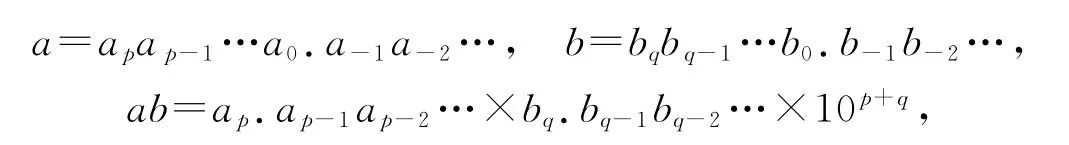
实际上就是先将a，b化为科学计数法的形式再作乘法.

由乘法的定义，显然乘法满足交换律.证明乘法满足结合律的方法是和加法类似的（由定义乘法时的讨论，只需考虑［1，10）上数，其它情况均可转化为这种情况，这里略去）.

定理6.1 乘法对加法满足分配律.

证即证a（b＋c）＝ab＋ac.与定义乘法时的讨论类似，这里只需考虑a是［1，10）上的数的情况.b，c仍用新的展开方法展开.Ak定义同定义乘法时的定义，Bk，Ck定义同定义加法时的定义.显然b＜0时，存在正整数N，使得0＜b＋N＜10，且存在m≥2，使得N＜10m.

先证明此时a（b＋N）＝ab＋a N.

令B′k＝Bk＋N，则

b≥0时用类似的方法也可以证明a（b＋N）＝ab＋a N.现在证明b＞0，c＞0时，

因为若b＞0，c＞0时有a（b＋c）＝ab＋ac，则当b，c不都大于零时，存在M，N∈NN，使得0＜b＋N＜10，0＜c＋M＜10，有

当b，c不都大于零时也有a（b＋c）＝ab＋ac.

设Bk，Ck＜10m，m≥1，则

定理6.2 上述定义的实数系统具有幺元.

证只需证明1是幺元即可.对任意的a∈RR，若a＝0，显然1×a＝1×0＝0＝a.否则与定义乘法时类似，只需考虑［1，10）上的数a＝a0.a1a2…，Ak定义同乘法时.

而Ak≤a＜Ak＋10-k，由闭区间套原理可知只能a×1＝a.

定理6.3 上述定义的实数系统具有逆元.

证与定义乘法时类似，仍只需考虑［1，10）上的数a.若a＝1，则显然a-1＝1.下设a∈（1，10）.由引理1，存在唯一的n∈ZZ，使得n a≤1＜（n＋1）a.而0×a≤1＜1×a，故n＝0.由引理1，存在唯一的a1∈ZZ，使得a1×10-1×a≤1＜（a1＋1）×10-1×a，且a1∈｛0，1，…，9｝.继续向下做，存在唯一的a2∈ZZ，使得

若存在k，当n＞k时an＝9，且k≠0时ak≠9.故存在n＞k，

则对任意的n＞k，有（0.a1a2…ak＋10-k）×a-1≤10-n×a，这不可能，故不会出现假设的那种情况.

令a-1＝0.a1a2…，则

由闭区间套原理，只能a a-1＝1.

而定义加法、乘法时定义的Ak，Bk都是Cauchy列，故这样定义的实数和用Cauchy列定义的实数是一样的.

［1］ 卓里奇B A．数学分析［M］．北京：高等教育出版社，2006：51-53．

［2］ Robert S Strichartz．The way of analysis（Jones and Bartlett Books in Mathematics）［M］．Sudbury：Jones ＆ Bartlett Publishers，2000：56-59．

The Infinite Decimal Expansion of the Real Numbers Definedby the Cauchy Sequences of Rational Numbers

CHEN Tong-zhou， XU Bin
（University of Science and Technology of China，Hefei 230026，China）

We discuss an equivalent of the real numbers defined by the Cauchy sequences of rational numbers，theinfinite decimal expansion．We also define the arithmetic operations as well as the order on it and prove that the definitionsare consistent with the original ones．

infinite decimals；real numbers；arithmetical operations

O171

C

1672-1454（2011）04-0186-06

2010-04-28