基于秩亏损的近场源定位快速算法
2011-11-09吴云韬
汪 海,吴云韬
(武汉工程大学智能机器人湖北省重点实验室,湖北武汉430074)
基于秩亏损的近场源定位快速算法
汪 海,吴云韬
(武汉工程大学智能机器人湖北省重点实验室,湖北武汉430074)
为避免近场源参数估计中的搜索计算,提出了一种改进的Root-MUSIC算法.该算法把阵列分成两个对称的子阵,并利用两个子阵信号子空间的广义旋转关系得到信号源角度的估计,然后利用估计出的角度和GESPRIT方法给出距离的估计.该方法在低信噪比下性能优越,能完成参数的自动匹配,且无需谱峰搜索计算复杂度低.仿真结果表明了此算法的有效性.
Root-MUSIC;近场源;距离估计;角度估计
0 引 言
空间谱估计是近三十年来发展起来的新兴信号处理理论,它在雷达、通信、声纳等领域有着众多的应用,而空间信号源的波达方向估计是其研究的一个重要方向.
在近场源参数估计中,许多研究方法相继被提出,如最大似然方法[1]、二维MUSIC方法[2]、一维MUSIC方法[3]等,最大似然方法的估计性能最好,但是需要进行多维谱峰搜索,计算复杂度很高;二维MUSIC方法的估计性能比较高,但是需要搜索谱峰和参数匹配;一维MUSIC方法虽然可以完成参数的自动配对,但仍需要一维搜索,计算复杂度较高.现有的方法中,ESPRIT-like方法[4],二级 MUSIC[5]和加权线性预测方法(WLP)[6]等能够直接给出参数的闭式解且精度比较高,但是ESPRIT-like和二级MUSIC[5]需要构造高阶累积量,其计算复杂度仍然很高;WLP算法需额外的参数配对,在信源参数比较接近时可能会配对失败.文献[7]提出了一种利用对称阵元结构的GESRPIT参数估计方法,有着较好的估计性能,但是需要2次一维参数搜索,计算复杂度很高,并且构造的谱函数在低信噪比下会出现谱峰数小于真实信号个数或伪峰过高而导致角度搜索失败的问题,从而导致整个参数估计的性能下降.文献[8]针对文献[7]中的角度搜索给出了一种闭式解,并且提出了利用聚焦方法来估计信号源的角度,但是在距离的估计中却仍然需要搜索计算,另外,聚焦方法需要利用基于波束形成的方法进行预估计,一定程度上限制了其实际应用.文献[9-10]分别提出了一种关于频率、角度和距离的联合估计新算法,文献[9]无需参数匹配,对角度和频率的估计比较好,而且还可以很好的分辨多个空间分布很近的信号源,但是其对距离的估计精度较差,文献[10]提出了一种基于平行因子分析的算法,该算法参数自动匹配,计算量小,但是在低信噪比下性能损失严重,无法解决弱信号环境下的信源定位问题.针对以上参数化估计[11]的情况,改进了文献[7-8]中提出的基于GESPRIT技术的近场源定位方法,给出了一种适用于高斯白噪声环境下的近场源参数估计快速算法,该方法无需搜索计算因而计算量低,仿真结果表明在低信噪比情况下也能给出很好的估计性能,且估计出的二维参数能自动匹配.
1 信号接收模型和子空间特征分解
考虑近场接收信号情况,如图1所示,K个非相干信号入射到N(奇数)个阵元组成的均匀线阵,阵元间距d≤,λ为载波的波长.通常,阵列信号矢量可以表示为:


s(t)=[s1(t),s2(t),…,sk(t)]T是信号的复包络矢量,噪声矢量n(t)=[n1(t),…,nN(t)]T.由式(1)得到阵列相关矩阵:

式(2)中,Rss为信号相关矩阵,σ2为噪声功率,H表示共轭转置.由于假定K个信号不相干,故Rss是可逆的.对Rxx进行特征分解有:

式(3)中,Us∈C(2M+1)×K张成了Rxx的信号子空间,对角矩阵∧s∈CK×K是对应Us的特征值.类似地,Un∈C(2M+1)×(2M+1-K)张成了Rxx的噪声子空间,对角矩阵∧n∈C(2M+1-K)×(2M+1-K)是对应Un的特征值.
2 近场源角度估计
文献[7]中提出了一种基于谱峰搜索的算法,但其计算复杂度较高.为了减小计算复杂度,文献[8]中给出了一种基于对称阵元结构的Root-MUSIC方法,这种基于秩亏损的方法最初在文献[12]中用于远场源参数估计.
将信号子空间Us作如下划分后得到Us1和Us2.

式(4)中,L=K+1,…,N-1表示子阵中阵元的个数.由式(1)和式(3)可知,存在一个K×K的满秩矩阵G使得Us=AG成立.
类似地,对应于第一个子阵和第二个子阵的Us1和Us2满足关系:
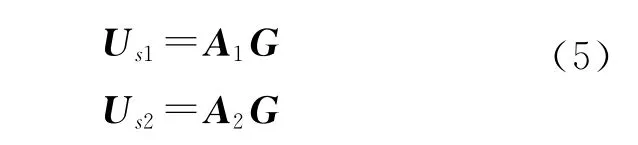
式(5)中,矩阵A1和A2分别是A的前L行和A的后L行.
根据阵元配置的对称结构有如下关系成立.

根据广义的ESPRIT方法[3],引进一个对角矩阵:

当θ=θk时,M的第k列将会变成0,这意味着矩阵M的秩等于K-1.J是交换矩阵,其副对角线上的元素全为1,而其它位置上的元素均为0.
考虑到M的秩亏损特性和Ψ(θ)中幂的线性变化.令z=e-j(4πd/λ)sinθk,式(8)变为:

方程式(11)的根中包含真实信号的角度信息.这里W∈C(2M+1)×K是任意的列满秩矩阵.式(11)有2(L-1)个根,其模最靠近单位圆的K个根α1,α2,…,αK对应K个信号源的角度θ1,θ2,…,θK.于是

3 近场源距离估计
关于距离估计,文献[7-8]都给出了一种基于谱峰搜索的估计方法.这里,作者给出一种基于秩亏损的闭式参数估计方法.
考察A1和A2的结构,有

4 仿真结果

把阵列划分成两个子阵,每个子阵由L=8个阵元组成.为了比较本文算法与文献[7]与文献[9]中的算法在不同信噪比SNR(Signal to Noise Ratio)下的均方根误差(RMSE),设定快拍数为400次,并进行了500次Monte Carlo实验.实验结果如图2~5所示.

图2 信源1角度的估计性能Fig.2 Angle estimation performance of sources 1

图3 信源2角度的估计性能Fig.3 Angle estimation performance of sources 2

图4 信源1距离的估计性能Fig.4 Range estimation performance of sources 1

图5 信源2距离的估计性能Fig.5 Range estimation performance of sources 2
图2、3所示的是两信源角度估计的RMSE随SNR的变化.图4、5所示的是两信源距离估计的RMSE随SNR的变化,分别对应信源1和信源2.
图2和图3中的CRB下界均由文献[9]给出.由图2、3可以看出,本文的算法性能在-10 d B到-5 dB时依然能保持良好,较文献[9]小5 dB左右.随着信噪比的增加,本文算法的优势越来越明显.SNR达到15 dB以后,文献[9]的性能已经没有明显的增加,这就是前面提到的参数估计的收敛性能较差.本文算法较文献[7]的算法,从-10 dB到15 d B二者参数估计的均方根误差都非常相近.这里说明一下,当SNR大于15 dB时,文献[7]的算法比本文的算法估计性能差,主要是由参数搜索的步长导致的.在仿真中,角度搜索步长设定为0.000 4π,距离搜索步长为0.000 2λ,从这二个数据中可以很明显的发现本文算法的优势,即计算复杂度低.为了定量的分析算法的运行时间,仿真用500次独立运行得出文献[7]算法的平均耗时为1 761.3 ms,而本文算法的平均耗时为5.3 ms,同样的文献[9]的平均耗时为1.8 ms.
文献[7]中的算法虽然需要谱峰搜索,但是却可以保证其估计的精度,如果搜索步长足够小,其性能曲线和本文算法曲线是相同的.给出闭式解的参数估计大多是靠牺牲一部分估计性能而让计算复杂度降低,如文献[9].而本文的算法能够在降低计算复杂度的同时又不损失估计的精度,这就是本文算法的优势所在.
5 结 语
基于接收阵列的对称结构,给出了一种快速的近场源参数估计新算法,无需额外的参数匹配.通过两次利用阵列导向矢量的结构和秩亏损的思想并基于GESPRIT方法估计出近场源的两维参数.与文献[7,8]中的算法相比,本文算法不需要谱峰搜索,能够直接给出闭式解,极大的减少了算法的计算复杂度.与文献[9]相比本文算法在没有严重损失计算复杂度的前提下得到很好的估计性能.
[1] Swindlelhurst A L,Kailath T.Passive direction of arrival and range estimation for near-field sources[C]//The 4th annual ASSP Workshop on Spectrum Estimation and Modeling.Minneapolis,MN USA:IEEE Press,1988:123-128.
[2] Huang Y D,Barkat M.Near 2 field multiple sources localization by passive sensor array[J].IEEE Trans on Antennas and Propagation,1991,39(7):968-975.
[3] Weiss A J,Friedlander B.Range and bearing estimation using polynomial rooting[J].IEEE J Ocean Engr,1993,18(2):130-137.
[4] Norman Yuen,Friedlander B.Performance analysis of higher order ESPRIT for localization of near-field sources[J].IEEE Trans on Signal Processing,1998,46(3):709-719.
[5] Liang Junli,Liu Ding.Passive Localization of Mixed Near-Field and Far-field Sources Using Two-stage MUSIC Algorithm[J].IEEE Trans.Signal Process,2010,58(1):108-120.
[6] Grosicki E,Abed-Meraim K,Hua Y.A weighted linear prediction method for near-field source localization[J].IEEE Trans Signal Process,2005,53(10):3651-3660.
[7] Zhi W,Chia M Y-W.Near-field source localization via symmetric subarrays[J].IEEE Signal Processing Letters,2007,14(6):409-412.
[8] Hong Yanghe,Wang Yide,Saillard J.Near-Field Source Localization by Using Focusing Technique[J].EURASIP Journal on Advances in Signal Processing,2008(10):1155-1163.
[9] Liang Junli,Zeng Xianju.A computationally efficient algorithm for joint range-DOA-frequency estimation of near-field sources[J].Digital Signal Processing,2009(19):596-611.
[10] 梁军利,王诗俊,高丽,等.一种无需参数配对的近场源定位新算法[J].电子学报,2007,35(6):1122-1127.
[11] 张煜东,颜俊,王水花,等.非参数化估计方法[J].武汉工程大学学报,2010,32(7):99-106.
[12] See C M S,Gershman A B.Direction-of-arrival estimation in partly calibrated subarray-based sensor rrays[J].IEEE Trans Signal Proces,2004,52(2):329-338.
[13] Hoole P R P.Smart Antennas and Signal Processing for Communications,Biomedical and Radar Systems[M].Southampton,U K:WIT Press,2001.
signal model for near-field source
Fast algorithm for near-field source localization by using rank reduction technique
WANG Hai,WU Yun-tao
(Key Lab of Intelligent Robot in Hubei Province,Wuhan Institute of Technology,Wuhan 430074,China)
A Root-MUSIC-based algorithm for near-field source parameter estimation is improved against the disadvantages of available spectral search computation.Firstly,the elevation angles of sources are estimated using the existing method based on the symmetric structure of array;and then substituting the estimated source elevation into the array manifold,the corresponding ranges are estimated by using the generalized ESPRIT(GESPRIT).This method results in automatically match of the parameters and is computationally efficient compared to spectral search methods.Simulation results show the effectiveness of this algorithm.
Root-MUSIC;near-field source;range estimation;angle estimation
陈小平
TN911.72
A
10.3969/j.issn.1674-2869.2011.11.016
1674-2869(2011)11-0062-04
2011-09-29
国家自然科学基金(60802046;61172150)
汪 海(1985-),男,安徽合肥人,硕士研究生.研究方向:阵列信号处理.
指导老师:吴云韬,男,教授,博士,硕士研究生导师.研究方向:阵列信号处理、自适应信号处理中的信号检测和参数估计、智能信息处理、无线传感器网络中的定位技术等.
图1 近场源信号接收模型 Fig.1
