倾转旋翼气动优化设计

薛立鹏，张呈林

(南京航空航天大学直升机旋翼动力学重点实验室，江苏 南京 210016)

0 引言

倾转旋翼机兼有直升机和固定翼飞机的特点，其旋翼需要工作在直升机和飞机模式下;而衡量倾转旋翼性能优劣的指标是悬停效率和巡航效率。在悬停状态下旋翼产生的拉力需要平衡全机重量及旋翼尾流对机翼产生的向下载荷，在前飞状态下旋翼所需的拉力仅需要用来克服整个飞机所产生的阻力，桨叶弦长和预扭角分布对这两种状态下的旋翼拉力和功率有重要影响;薄翼型具有较高的阻力发散马赫数和较小的升力系数，厚翼型则相反，因此在桨叶厚度的选择上，桨根采用厚翼型而桨尖采用薄翼型以使得桨叶具有较大的升力系数和较高的阻力发散马赫数;旋翼转速的选择范围受限于旋翼轴的最大扭矩和最大桨尖速度，另外转速的选择也影响到压缩性的大小［1－3］。在给定发动机功率的情况下，需要对倾转旋翼桨叶的弦长、预扭角、厚度及翼型分布位置和旋翼转速进行优化，以使旋翼具有优良的悬停效率和巡航效率。准确计算倾转旋翼的气动性能的关键是如何有效地确定桨叶任意剖面处的诱导速度，而倾转旋翼桨叶具有展弦比小，负扭转大的特点，本文采用自由尾迹方法建立了倾转旋翼的气动特性分析模型，考虑弦长变化和负扭转的影响［4］，记入了尾迹及其收缩对诱导速度的影响，能够准确地描述桨叶诱导速度的分布，气动性能的计算具有很好的精度。本文的优化问题属于多目标优化问题，采用了基于协同机制的多目标优化策略和遗传算法优化求解;优化后旋翼性能得到了明显的提高。

1 基于自由尾迹方法的倾转旋翼气动特性分析

自由尾迹分析方法［5－6］是在确定尾迹几何形状及涡线环量的基础上，由Biot－Savart定律积分得到诱导速度的分布。旋翼气动模型采用二阶升力线理论，即Weissinger－L升力面理论，桨叶沿展向按余弦分成若干小段，在每小段上附着环量为常值，每片桨叶用四分之一弦线上附着涡代替，附着环量沿展向变化引起尾随涡系从桨叶后缘托出，形成近尾迹，近尾迹后接远尾迹，它是外部近尾迹聚集成的一条自由的集中涡线，控制点位于四分之三弦线与桨段中线的交点处，通过 Kutta－Joukowski定理把桨叶升力与附着涡环量关联起来。引入固定坐标系(x，y，z)和旋转坐标系(x，y，z)，固定坐标用来描述尾迹位置和几何形状，而旋转坐标系用来描述桨叶当地的气动环境，坐标系及尾迹模型见图1。

图1 旋翼坐标系及尾迹模型Fig.1 Coordinate and wake model of rotor

桨叶环量的求解利用了由叶素理论和 Kutta－Joukowski定理计算的桨叶剖面气动力相等的条件［7］，避免了单由桨叶表面法向速度为零的边界条件［8］求解桨叶环量与由基于二维翼型数据的叶素理论计算的气动力不一致的问题，充分利用了基于试验得到的二维翼型的气动数据，计算结果更为可靠。为了求解桨叶环量，需要确定尾迹形状。尾迹分离点在总体坐标中的位置向量为(ψ，ζ)，其中ψ 为桨叶方位角、ζ为尾迹角，它以当地的速度自由移动，单根涡线的控制方程可以写为:

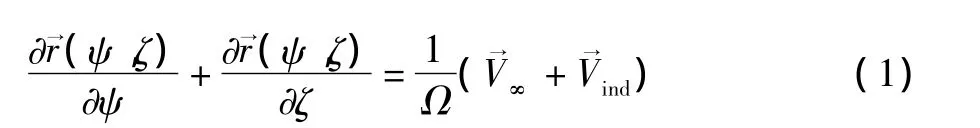
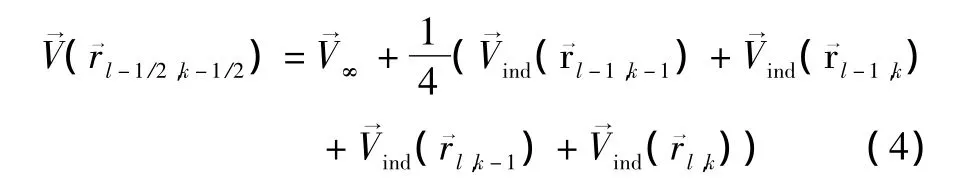
取△ψ=△ζ，将式(2)(3)(4)代入方程(1)可得递推关系式:

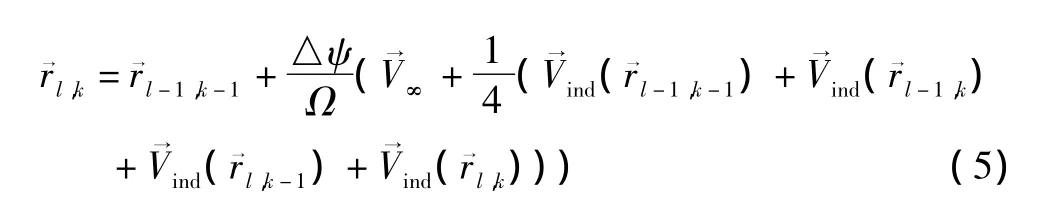
这里采用文献 ［6］中提出的伪隐性预估修正算法和涡核修正模型求解。进行尾迹迭代求解时，必须给尾迹点位置初始化并设置边界条件，当计算域中所有尾迹分离点都通过式 (5)计算了一遍，这样便完成一次尾迹迭代，直到前后两次迭代尾迹分离点位置之差小于要求的精度，尾迹形状便可以确定下来，由此可求得旋翼的拉力和功率，进而可以求得悬停和巡航效率:这里 CT为拉力系数，CQ为需用功率系数，J为前进比。

本文以XV－15全尺寸倾转旋翼为算例，采用上述方法，分析计算了旋翼气动特性。并将本文计算方法得到的结果与XV－15全尺寸风洞试验数据［8－9］进行了比较，见图2。

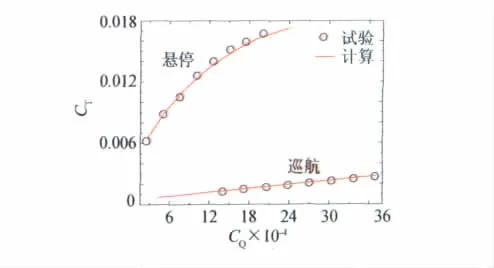
图2 XV-15悬停时拉力随功率变化Fig.2 Comparison of XV-15 aircraft＇s thrust coefficient vs.torque coefficient in hover and cruise

以上分析表明本文所采用气动模型是正确的，可以用于倾转旋翼的气动特性计算。

2 倾转旋翼桨叶多目标优化设计

倾转旋翼桨叶沿展向分布着4种不同翼型，第一种翼型(NACA64－528)布置在桨叶根部和rstation1之间，第二种翼型(NACA64－118)布置在 rstation1和 rstation2之间，第三种翼型(NACA64－(1.5)12)布置在 rstation2和 rstation3之间，第四种翼型(NACA64－208)布置在rstation3和桨尖之间，桨叶的弦长和预扭角定义为立方分布，桨叶厚度分布定义为平方分布，桨叶微段质量与弦长二次方成正比，沿展向变化如下:

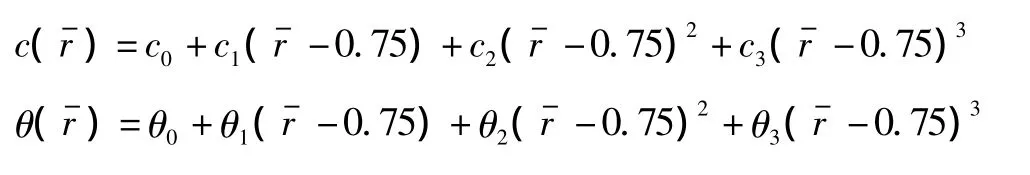
2.1 多目标优化问题的描述

1)优化目标:

以悬停效率和巡航效率的最大化为优化目标

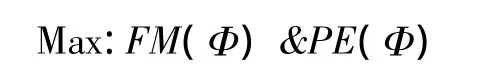
2)优化设计变量:

(1)桨叶翼型分布位置:rstation1，rstation2，rstation3

(2)弦长分布系数:c0、c1、c2、c3

(3)扭转角分布系数:θ0、θ1、θ2、θ3

(4)厚度分布系数:t0、t1、t2

(5)旋翼转速:Ωhover、Ωcruise(RPM)

3)约束条件:

(1)在优化过程中，悬停和前飞时每步迭代均分别用载荷系数 CT/σ =0.144和 CT/σ =0.06配平旋翼，保证每次迭代产生一个可行解，前飞速度为154.32m/s(300节)。

(2)旋翼功率系数 (Cp≤CPref(CPref=0.0157)，桨叶总重 Wblade≤Wref(Wref=164.49)，桨叶弦长(0.001≤c/R≤0.5)、预扭角(－ 15°≤θ≤45°)、厚度(0.05≤t/c≤0.4)及翼型分布位置的取值范围(0.15≤rstation1≤0.45，0.5≤rstation2≤0.65，0.65≤rstation3≤0.9)，旋翼转速(400≤Ωhover≤450，550≤Ωhover≤600)。

4)优化方法及策略:

倾转旋翼气动优化设计是多变量、多约束、多目标、非线性强的复杂计算过程，计算量较大，优化之前首先分析了桨叶气动参数对于倾转旋翼悬停效率和巡航效率的灵敏度。

由图3可见倾转旋翼悬停效率敏感于桨叶弦长变化，巡航效率敏感于桨叶扭转变化，基于此分析本文采用了基于协同机制的多目标优化策略［10］来处理该优化问题，将设计变量按照其对悬停和巡航的灵敏度影响分配到不同的系统中，以减少系统和子系统的设计变量，明确寻优参数，提高优化效率。优化框架见图4，其思想就是将多目标优化问题按照协同优化框架进行分解为系统级和子系统级，然后采用协同优化方法进行优化求解。系统级优化目标为悬停效率和巡航效率，约束为一致性约束，设计变量包括共享设计变量耦合设计变量状态设计变量分别表示悬停和前飞时旋翼配平的总距，系统级的优化采用改进的多目标遗传算法(NSGA－II)，NSGA－II算法采用个体分层排序，并引入拥挤度算子和保优机制，在选择操作前，先基于Pareto优劣性对种群进行分层排序，在第一层的个体具有最大的适应值，优先被复制入下一代，经选择后参加繁殖的个体所产生的后代同其父代个体共同竞争来产生下一代种群，因此有利于保持优良的个体，迅速提高种群的整体水平;子系统1优化目标为F1，设计变量为Xl1，约束Gl1为Xl1的相关约束，子系统2优化目标为F2，设计变量为Xl2，约束Gl2为Xl2的相关约束，子系统级优化采用标准的遗传算法。

图3 桨叶参数对悬停效率和巡航效率的灵敏度分析Fig.3 Parameter sensitivity analysis of blade on figure of merit and propulsive efficiency

2.2 优化结果

根据前面定义好的优化问题，按照倾转旋翼气动多目标协同优化框架集成系统和子系统优化模型，图5给出了优化目标的优化迭代历程，目标函数在经历40次优化迭代后趋于收敛。表1列出了相关的优化摘要，给出了多目标优化结果(排序前5的Pareto非劣解集)。从倾转旋翼的悬停效率和巡航效率的优化历程来看，二者之间是矛盾的，优化迭代是一个折衷寻优的过程;以第一组为决策者最终设计参数，在满足约束条件的情况下，优化后的悬停效率比基准值提高了6.66%，巡航效率比基准值提高了5.95%，巡航功率降低了1.3%，桨叶重量减轻了2.3%，旋翼整体性能得到了提高。

3 结论

(1)本文针对倾转旋翼桨叶展弦比小，负扭转大，采用几种不同翼型的特点，建立了基于自由尾迹的倾转旋翼气动特性分析方法，能很好地计算倾转旋翼机在悬停和巡航时的气动性能。

图4 倾转旋翼气动多目标协同优化框架Fig.4 Multi-objective collaborative optimization schematic of tilt-rotor aerodynamic design

(2)将倾转旋翼的气动优化问题归纳为有约束的非线性多目标优化问题，在分析桨叶参数对倾转旋翼效率影响的灵敏度基础上，采用基于协同机制的多目标优化策略和遗传算法求解，与原XV－15倾转旋翼相比，在满足约束条件的情况下，优化之后倾转旋翼具有更优的气动性能，所采用的优化方法是有效可行的。

(3)倾转旋翼机的研制在我国还处于探索阶段，本文的分析方法可以用于倾转旋翼气动参数优化设计，为今后开展倾转旋翼气动设计提供了技术支持。

图5 悬停效率和巡航效率优化历程Fig.5 Multi-objective optimization runcounter

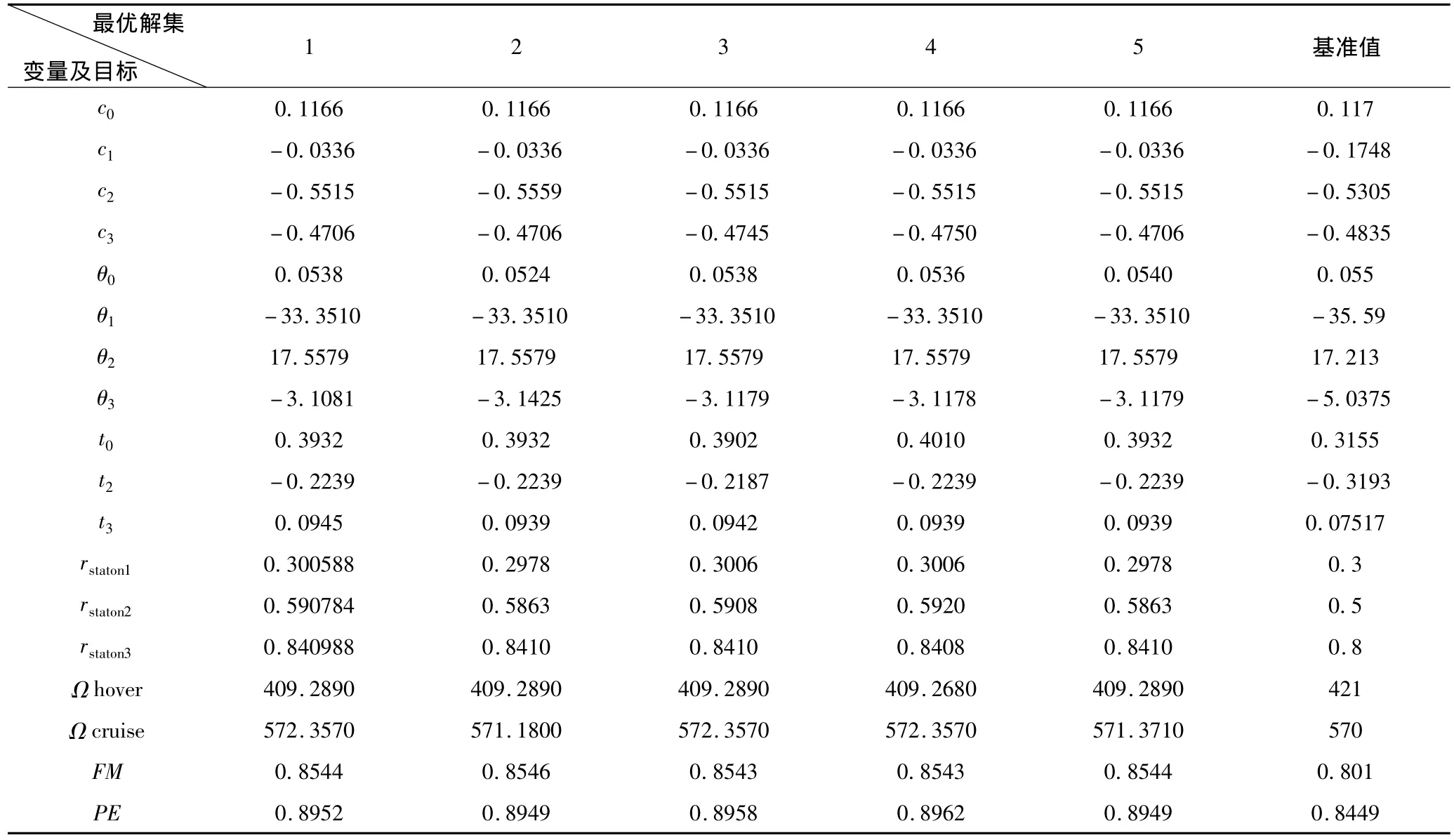
表1 优化摘要Table 1 Summary of optimization results

［1］ÖMER SOYKASAP.Aeroelastic optimization of a composite tilt rotor［D］.Georgia:Georgia Institute of Technology，1999.

［2］MARTIN STETTNER.Tilt rotor multidisciplinary optimization［D］.Georgia:Georgia Institute of Technology，1995.

［3］ROGER L SMITH.Closed－foam equations for the lift，drag，and pitching－moment coefficients of airfoil sections in subsorric flow［R］.AVRADCOM Twhntcal Report 78－15(AM).California:AVRADCOIM Research and technology Laboratories Ames Research Center，(10 ～21).

［4］BAGAI A，LEISHMAN J G.Rotor free wake modeling using a pseudo implicit technique－including comparisons with experimental data［J］.Journal of the American Helicopter Society，1995，40(3):29 －41.

［5］MAHENDRA J BHAGWAT.Mathematical modeling of the transient dynamics of helicopter rotor wakes using a time－accurate free－vortex method［D］.Maryland:The University of Maryland，2001.

［6］ASHISH BAGAI.Contributions to the mathematical modeling of rotor flow－fields using a pseudo－implicit free－wake analysis［D］.Maryland:The University of Maryland，1995.

［7］李春华，徐国华.悬停和前飞状态倾转旋翼机的旋翼自由尾迹计算方法［J］.空气动力学学报，2005，23(2):152－156.

［8］THOMAS ROBERT MCCARTHY.A new higher－order composite theory for analysis and design of high speed tilt－rotor blades［R］.NASA Contractor Report No.CONTRACT NAG2－771，Arizona:Arizona State University，(120～130).

［9］ADITI CHATTOPADHYAY and THOMAS R MCCARTHY.An integrated optimum design approach for high speed prop rotors［R］.Final Report on NASA AMES GRANT No.NCC2－795，Arizona:Arizona State University，(4 ～25).

［10］TAPPETA R V，RENAUD J E.Multiobjective collaborative optimization［J］.Journal of Mechanical Design，1997，9(119):403－410.