一种新的间断侦测器及其在DGM中的应用
2011-11-08张来平贺立新邓小刚张涵信
张来平,刘 伟,贺立新,邓小刚,张涵信
(1.中国空气动力研究与发展中心 空气动力学国家重点实验室,四川 绵阳 621000;2.中国空气动力研究与发展中心,四川 绵阳 621000)
0 引言
真实的流动是很复杂的,流场中常常会有激波、旋涡、分离等现象。为了模拟这些复杂的流动现象,高精度格式构造方法越来越受到CFD学者们的关注。在众多的高阶精度计算方法中,间断Galerkin有限元方法(DGM)备受关注。间断有限元方法是最早由Reed和Hill为解决中子运输方程而提出的[1]。在此基础上,特别是近年来,出现了种类丰富多样的DGM方法。DGM方法保持了传统有限元方法(FEM)和有限体积法(FVM)的优点,融入了高分辨率有限差分方法(FDM)和有限体积方法中如数值通量、Riemann间断分解、TVD和限制器等思想;同时它又是一种积分形式的计算方法,可以直接应用于非结构网格或混合网格,与其它数值方法相比,DGM具有突出的优势。
然而,高精度格式在激波附近会产生数值振荡,引起非线性的不稳定性,甚至出现非物理解,如负的压力和密度。Harten在1983年首次提出了总变差减小(total variation diminishing,TVD)的概念[2],为差分方法的高精度格式构造开拓了崭新的方向,并通过限制器(limiter)技术,构造出二阶TVD格式。限制器的作用是引入非线性效应。常见的限制过程是通过比较临近单元解的性态,使得重构的左右变量不至于“上冲”或“下冲”,以保证解的本质无振荡,我们把这种限制器称为梯度限制器(slope limiter),其本质上是对一阶导数进行限制,TVD格式和NND[3]格式均属此类,不同的是TVD格式是对原始变量或守恒变量进行限制,而原始NND格式限制于通量。
这类梯度限制器的缺陷在于对光滑的极值点附近也会起作用,从而降低了解的一致高精度。间断侦测器的作用就是侦测出激波所在的位置,从而只在“间断区域”引入限制器,其它的“光滑区域”仍然采用线性格式,以改善数值解的模拟精度。Chi-Wang Shu等[4]通过TVB函数判断出“问题单元”(trouble cell);S.Adjerid等的研究[5]指出,DGM在单元的出流边界具有很强的超收敛特性,并基于此特性构造了一种间断侦测器。
本文通过比较单元交界面的左右变量,构造了一种新的间断侦测器,并将该方法推广应用于一维和二维Euler方程的计算。首先利用间断侦测器侦测出“间断单元”(“问题单元”),然后对“问题单元”进一步引入梯度限制器,由于本文采用的是基于Taylor基的间断Galerkin方法,梯度限制器能够更直接地实现。针对一维问题,我们采用 minmid限制器[3],及其推广的 Moment限制器[6];二维情形采用鲁棒性更好的Barth限制器[7]。数值计算结果表明本文的间断侦测器能较好地捕捉“问题单元”,从而尽可能减少限制器对计算精度的影响,同时保证在强间断处没有非物理振荡。
1 间断侦测器和DG计算方法
基函数的选取对于间断Galerkin方法尤为重要,传统的DGM对于三角形/四面体采用面积坐标/体积坐标构造基函数,对于矩形单元则采用双线性插值构造基函数[8]。其它形状的单元则需要坐标变换至标准单元,格式中出现多种基函数,这使得限制器的构造,隐式时间推进,边界条件处理等都存在诸多不便。Luo Hong基于Taylor展开构造了一组Taylor基[9],其优势在于针对不同网格单元基函数的形式是一致的,能够简单方便地应用于带有“悬空”节点的混合网格,而这种情况在多层次的Cartesian网格和自适应网格中经常出现。并且Taylor基具有先天性的层次性,更有利于p-multigrid策略的实施。本文中DGM的基函数采用的是Taylor基,限于篇幅,这里不再赘述,具体内容可参考文献[9]。这里重点介绍在DGM计算过程中,为了有效捕捉激波等强间断的间断侦测器,以及在一维和二维情况下的限制器。
1.1 间断侦测器
DGM假设解是分段p次多项式,即使在光滑区域,通过左右单元插值得到的单元交界面的左右变量通常是不相等的,但它们满足:
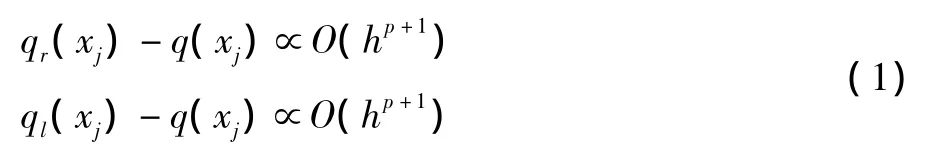
这里假设q(x)为精确解,xj为单元i的交界面上的第j个Gauss积分点,h为单元的特征长度。则
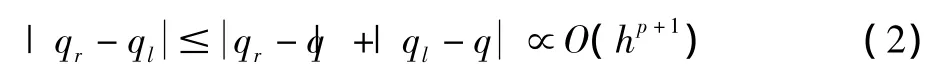
也就是说,在光滑区域,虽然假设单元交界面是间断的,但左右变量的差别是p+1阶小量。对于间断区域或大梯度附近,左右变量的差别是很大的,通常为|qr-ql|∝O(h)。
为了方便书写,我们记:变量q在xj的跳跃[q]j和平均分别为:
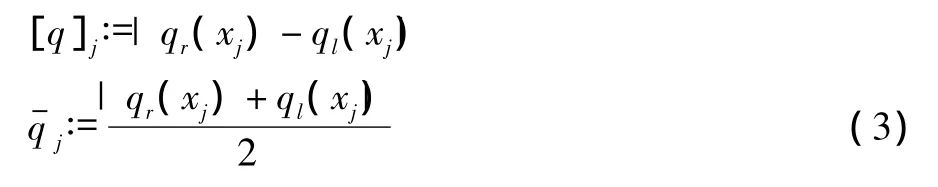
定义单元i的侦测因子

通过判断Di的大小,以确定“间断单元”,或称“问题单元(trouble cell)”:

θ为侦测阀值。(4)式中的Lp范数,在本文的算例中,均取L∞范数,即只要存在一个Gauss积分点的间断侦测因子大于侦测阀值,则这个单元为“间断单元”。本文沿用文献[5]中的方法,分别选用密度和熵作为侦测的对象。
1.2 DGM格式中的限制器
本文的算例中,一维问题采用Lilia Krivodonova构造的Moment限制器[6],二维问题采用Barth和Jesperson的梯度限制器[7]。
Moment limiter的基本思想是判断单元i的p阶导数与若干相邻单元的(p-1)阶导数,从高阶到低阶依次对p阶导数进行限制,避免直接对梯度限制而带来的过多耗散。在光滑区域,单元中心点的二阶导数满足(一维问题):
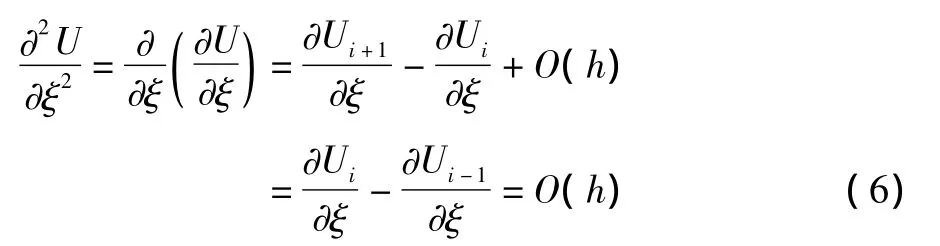
其中ξ为局部坐标。因此对二阶导数采用如下限制:
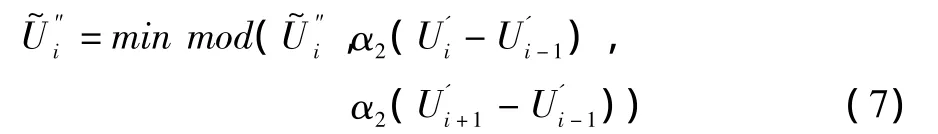
同理对一阶导数

如果二阶导数被限制了,则进一步限制一阶导数,否则不对一阶导数限制。这里的α1、α2为控制耗散的参数,它们的值越小,限制的强度越大,耗散也就越大,计算则更稳定。数值实验表明取 α2∈[1,10],α1∈[1,2]是合适的。
对于二维问题,我们采用Barth限制器。Barth限制器对梯度进行如下限制:
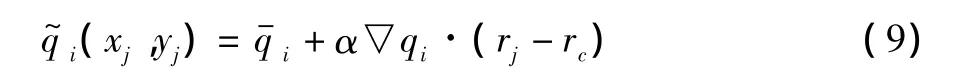
其中rc为单元中心点坐标,rj为边界上的Gauss积分点坐标。限制系数α定义为:
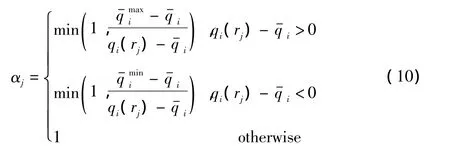
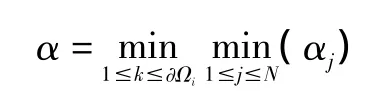
限制器可以针对守恒变量、原始变量或特征变量进行限制,一般来说,限制特征变量鲁棒性更好,而对守恒变量限制则更直接,不需要矩阵变换。本文中,限制的是守恒变量。对于高超声速问题,守恒变量型的限制器在数值通量的计算中,单元交界面左右的压力可能出现负值,导致无法计算当地声速。此时,我们用左右单元中心点的压强值代替交界面的压力。
2 一维Euler方程计算结果
2.1 算例1:Sod问题

Sod问题的初始条件由(11)式给出,在x=0.5处有初始的间断。在计算区域[0,1]上,共用101个网格点,计算0.20个时间单位。图1给出了p=1和p=2时利用DGM方法得到的计算结果,其中的“点标+和*”分别代表密度和熵侦测器侦测到的“问题单元”,可以看到,熵侦测器侦测到的“问题单元”较少。图2给出了密度和熵侦测器的侦测因子分布,可以看出,间断侦测器能够准确地捕捉到激波所在位置。比起熵侦测器,密度侦测器的侦测敏感度更强,由于熵值在接触间断处仍然是连续的,熵侦测器对接触间断没有响应,而密度侦测器在接触间断处也有反应(x≈0.23的位置)。

图1 DGM方法求解Sod问题的密度分布比较(T=0.20s,dx=1/100):(上)p=1;(下)p=2Fig.1 Density distribution for Sod problem with DGM,(Up)p=1;(Down)p=2

图2 Sod问题的密度和密度侦测因子分布(T=0.20s,dx=1/100)(上)p=1;(下)p=2Fig.2 The distribution of density and entropy indicators for Sod problem.(Up):p=1;(Down):p=2
2.2 算例2:Shu问题

Shu问题描述的是一个运动Mach数为3的激波和正弦波的相互干扰,从而诱发出高频扰动,被看作是激波与湍流相互作用的简化模型。该问题流场中含有明显的细致结构,对于考察计算格式对流场细节和广谱范围内的分辨率十分合适,一直是格式验证的标准算例。初始条件由式(12)给出,计算区域[-2,8]剖分为600个单元,时间演化至1.6个时间单位。图3给出了利用三阶DG方法(p=2)在不同的间断侦测器作用下的计算结果,从图3右边的放大图可以看出,不用间断侦测器时限制器将“抹平”峰值,而熵侦测器能给出与精确解更为符合的计算结果,因为其侦测到的“问题单元”较少。

图3 Shu问题的间断侦测器计算结果比较Fig.3 Shock detection for Shu problem.Left:Density indicator;Middle:Entropy indicator;
3 二维Euler方程计算结果
3.1 算例1:绕NACA0012翼型的跨声速流动
对于该外形,计算域采用非结构的混合网格进行剖分,即在壁面附近采用灵活性较好的三角形网格离散,而在外场采用非结构的Cartesian网格,如图4所示。网格单元总计5004个,其中三角形1100个,矩形单元2904个。计算方法采用了基于Taylor基的二阶精度DG格式,并利用Barth限制器抑制激波附近的波动。初始条件取来流马赫数为0.85,攻角为1.25°。在此计算条件下,翼型的背部和腹部均会出现激波。图5(a)给出了翼型壁面的压力分布,与Shu等人的计算结果吻合较好。从图5(b-c)给出的间断侦测器判断的“问题单元”分布情况,可以看出密度侦测器和熵侦测器都能够准确地判断激波所在的位置,对比熵侦测器,密度侦测器判断的“问题单元”更多,这和一维情形的结论一致。图6显示了两种侦测器得到的流场Mach数等值线,可以看到,计算给出了清晰的激波结构。
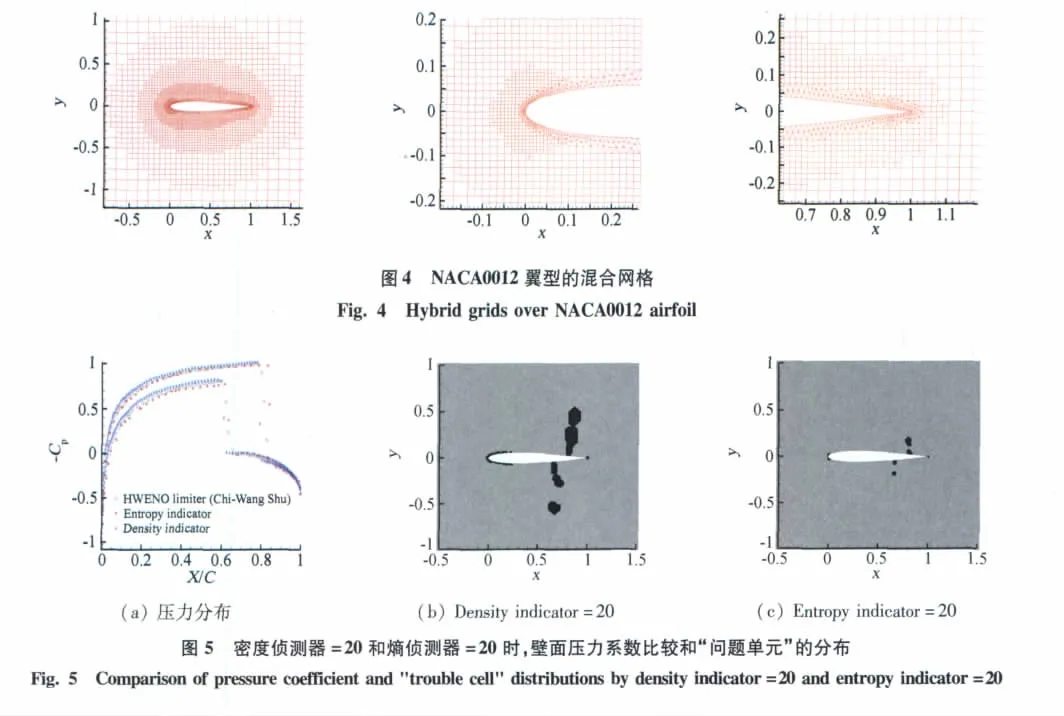
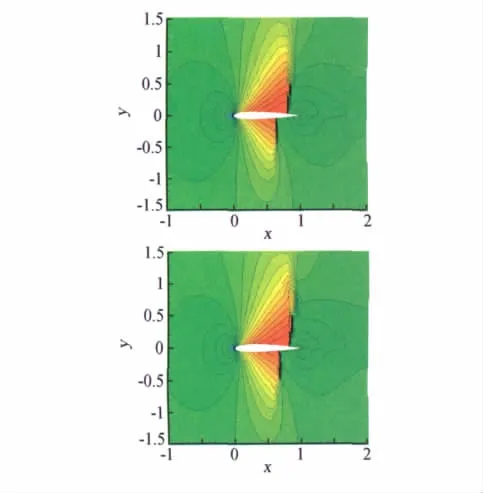
图6 NACA0012翼型跨声速绕流的Mach数等值线Fig.6 Mach number contours over NACA0012 airfoil
3.2 算例2:双马赫反射问题
该问题描述的是Mach数为10的强运动斜激波以与x轴方向呈60°角的方向入射,入射点在(1/6,0),计算区域取[0,4]×[0,1]。激波波前静止空气的密度为1.4,压力为1,波后按激波关系给定初始条件。下边界在x>1/6的区域给定壁面边界条件,其它边界区域按照激波运动所在的位置,分别给定波前或波后的值。时间推进至t=0.2。利用Barth限制器和本文构造的间断侦测器,网格密度为480×120。采用基于Taylor基的二阶DG方法(p=1)得到的计算结果如图7所示,从图中可以看出,引入间断侦测器后既能较好地捕捉强激波结构,又能给出比较精细的局部剪切结构。图8显示了两种间断侦测器侦测到的“问题单元”,同样地,熵侦测器侦测到的“问题单元”较少。图9显示了局部放大的流场结构,可以看到,在没有引入间断侦测器时,接触间断处的细致结构被限制器“抹平”,而采用间断侦测器后,流场结构的分辨率显著提高。
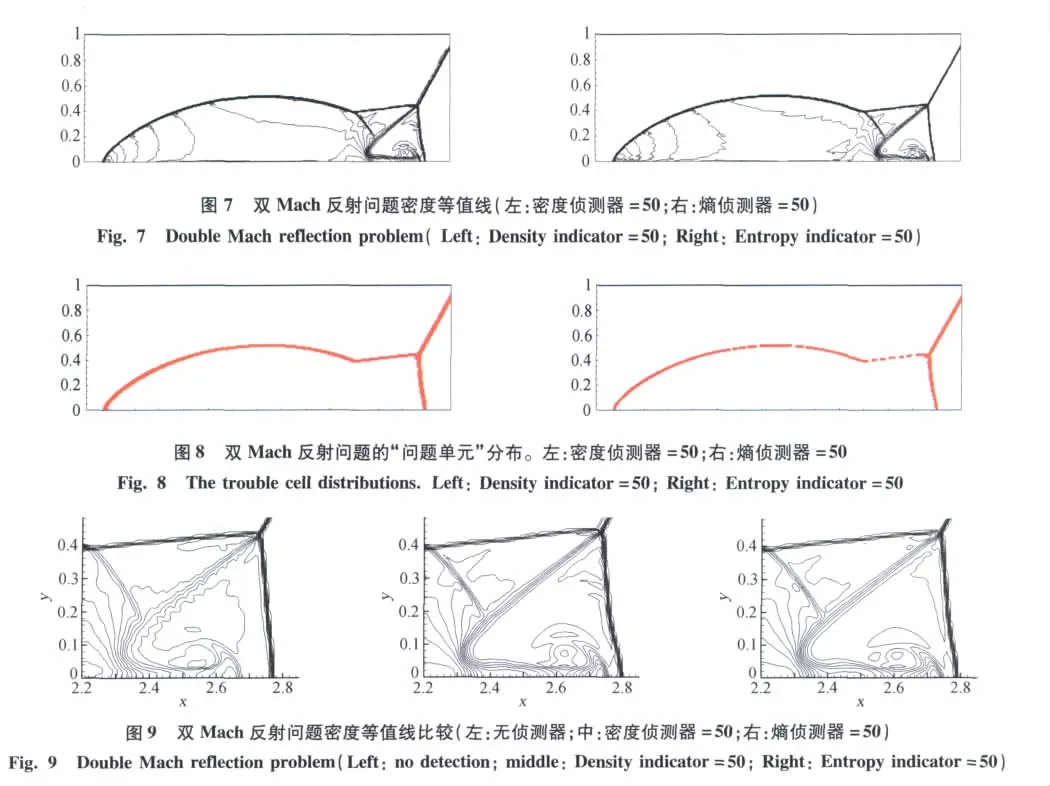
4 结论
本文根据单元交界面左右变量的差别,提出了一种新的间断侦测器构造方法。该间断侦测器的构造原理简单,编程实现容易。针对一维和二维Euler方程,我们将此间断侦测器用于间断Galerkin格式的数值计算中,通过与适当的限制器配合使用,可以有效抑制激波附近的数值振荡,并能保持在光滑区的计算精度。对一维的Sod问题、Shu问题,二维NACA0012翼型跨声速绕流、双马赫反射问题方程进行了数值实验,计算结果证明了方法的有效性。
[1]REED W H,HILL T R.Triangular mesh methods for the neutron transport equation[R].Technical Report LA -UR-73-479,Los Alamos Scientific Laboratory;1973.
[2]HARTEN A.High resolution schemes for hyperbolic conservation laws[J].Journal of Computational Physics,1983,49:357-393.
[3]张涵信.无波动、无自由参数的耗散差分格式[J].空气动力学学报,1986,6:143 -165.
[4]QIU J,SHU C W.Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous Galerkin method:one dimensional case[J],Journal of Computational Physics,2003,193:115 -135.
[5]ADJERID S,DEVINE K,FLAHERTY J and KRIVODONOVA L.A posteriori error estimation for discontinuous Galerkin solutions of hyperbolic problems[J].Computer methods in applied mechanics and engineering,2002,191:1097 -1112.
[6]KRIVODONOVA L.Limiter for high-order discontinuous Galerkin methods[J].Journal of Computational Physics,2007,226:879-896.
[7]BARTH T,JESPERSON D.The design and application of upwind schemes on unstructured meshes[A].In 27th Aerospace Sciences Meeting[C].AIAA 89 -0036,Reno,Nevada,1989.
[8]贺立新,张来平,张涵信.间断Galerkin有限元和有限体积混合计算方法研究[J].力学学报,2007,39(1):15-21.
[9]LUO H,BAUM J D,LOHNER R.A discontinuous Galerkin method based on a Taylor basis for the compressible flows on arbitrary grids [J].Journal of Computational Physics,2008,227:8875-8893.
