喷流控制飞行器气动参数辨识方法研究
2011-11-08王贵东崔尔杰陈则霖
王贵东,崔尔杰,陈则霖
(中国航天空气动力技术研究院,北京 100074)
0 引言
利用系统辨识理论和技术,对飞行试验测量数据进行气动参数辨识,是空气动力学研究的一个重要手段,在国内外都受到了广泛的重视。由于辨识得到的是飞行器在真实飞行过程中的气动参数,对于检验地面试验及理论计算结果,为飞行器控制系统提供正确的气动数学模型,分析飞行器气动特性和飞行品质,具有重要的意义[1]。喷流控制姿态是一种十分敏捷和有效的方法,为越来越多的高速飞行器所采用。特别是在高空,由于大气密度的降低,普通升力面则显得力不从心,喷流控制更具有其独特的优势。在很高的高空,喷流推力基本上是燃料燃烧产生的高速气体所带来的牛顿力学意义上的反作用力。在较低的高度,喷流与外流场之间会产生相互干扰,这种干扰可以产生作用在返回舱上的另一种力,即干扰气动力。如果能更精确地知道喷流干扰气动力以及与喷流环境因子之间的关系,那么用喷流对飞行器进行控制会更有效。
对于喷流的干扰效应,过去五十多年里已开展了大量的研究,主要采用理论计算和风洞实验的手段[2-3],并辅有少量的飞行试验。对于飞行试验,可以通过两种方法研究喷流干扰效应:一是通过测量喷流附近的压力,来分析喷流干扰效应,这是过去主要采用的方法[4];二是利用飞行器的运动响应数据,通过辨识获得喷流干扰产生的气动力,这方面的工作开展的还很少。上世纪六十年代,美国进行了“阿波罗”飞船飞行试验,并利用试验测量数据计算得到了一些有用的气动参数[5-6]。但是,受当时测量技术和辨识水平的限制,未能辨识气动导数和喷流控制力矩参数等。本文以某飞船返回舱为例,利用其飞行试验实测轨道数据,通过模型辨识和参数估计,获取气动力矩与喷流力矩模型。首先对飞行试验数据进行各种预处理,以尽可能地消除各种随机噪声和误差,并预估计力矩系数、攻角、侧滑角和马赫数等参数。进而根据上述参数,采用逐步回归方法,建立气动力矩模型和喷流力矩模型。最后,采用极大似然估计方法得到模型中的未知参数。辨识结果能够更好地预测观测量角速率和姿态角,有助于提高返回舱姿态控制的精度。该辨识方法是研究喷流干扰效应的一种有效途径。
1 参数预估计
在对力矩系数、以及攻角、侧滑角、马赫数等参数进行预估计前,需要对飞行试验测量数据进行各种预处理,包括剔除野值、插值加密、平滑滤波、数值微分、过载校正、坐标转换等,并综合利用内、外测数据对再入轨道进行重建,以尽可能地消除各种随机噪声和误差。数据预处理和轨道重建后,各参数之间具有很好的相容性,可以根据动力学方程和几何关系,直接估计攻角、侧滑角、马赫数和力矩系数等参数。
1.1 攻角、侧滑角的预估计
利用飞行速度和大气风速计算返回舱与气流的相对速度,并将其转换至体轴坐标系,根据体轴坐标系和气流坐标系的空间几何关系,则攻角和侧滑角的表达式为:
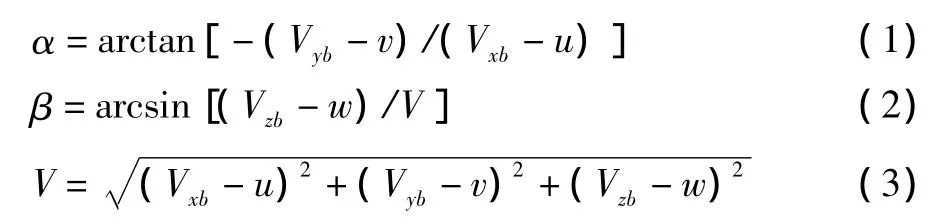
式中,Vxb、Vyb、Vzb为飞行速度的体轴系分量,u、v、w为大气风速的体轴系分量。
1.2 力矩系数的预估计
由预处理和重建后的飞行试验数据,可以预估总力矩系数。

其中,ω =[ωx,ωy,ωz]T为返回舱姿态运动角速率;为角加速率,由角速率微分得到;MI为转动惯量矩阵;q、S、L分别为动压、参考面积和参考长度。
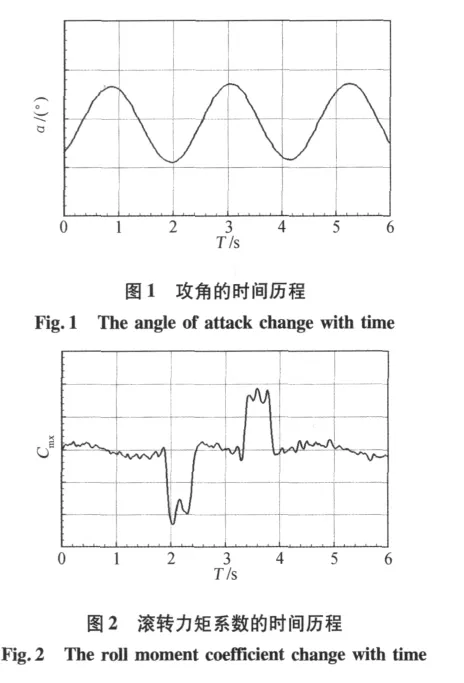
图1和图2分别给出了攻角和滚转力矩系数的估计结果。预估计的攻角、侧滑角、马赫数和力矩系数等参数作为后续气动建模的输入数据。
2 气动与喷流力矩建模
本文采用多项式形式的力矩模型,并采用逐步回归方法对模型的候选因子进行筛选,以建立最优的气动与喷流力矩模型。考虑到返回舱在超声速和高超声速段主要对滚转进行控制,故本节仅对滚转控制条件下的气动与喷流力矩进行建模。
2.1 力矩模型的数学描述
根据空气动力学理论,在无喷流控制条件下,返回舱气动力矩的大小与高度、马赫数、攻角、侧滑角和角速率等飞行状态参数有关,上述参数及其有限的高阶项、交叉项均可以作为气动力矩模型的候选因子。返回舱再入飞行时,马赫数与高度线性相关,故只考虑马赫数的影响。以滚转力矩系数模型为例,其一般形式为:
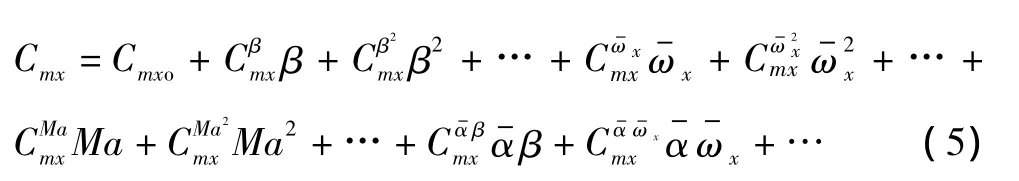
当喷流发动机工作时,除气动力矩外,返回舱还受到喷流力矩的作用。喷流力矩具有如下特点:
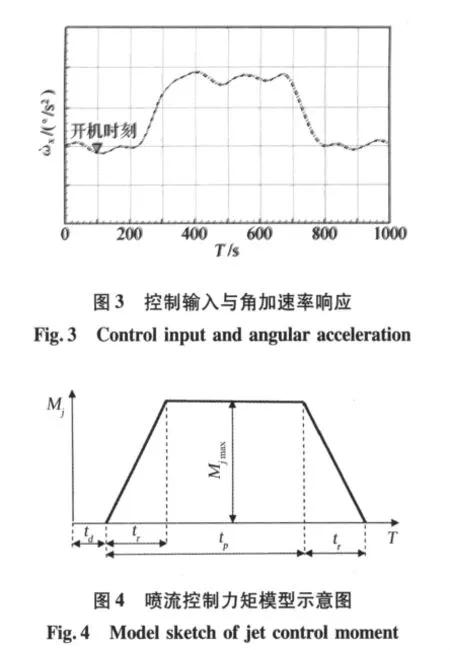
(1)喷流力矩在时间上存在滞后(如图3)。本文采用时间参数td来描述滞后时间,在力矩建模阶段,该参数可以根据发动机开关机状态与角加速率的相位关系确定,在进行参数估计时则作为待估计的未知参数;
(2)喷流力矩的产生和消失是一个动态变化的过程。本文根据发动机的地面测力结果,结合喷流作用下角加速率的响应历程,将力矩的这一动态变化过程近似地描述为一个线性过程,用发动机开关机状态参数Jx在[0,1]内线性变化来表示,在一个脉冲周期内有

式中,tr称为过渡时间,tp为脉冲长度。
(3)喷流力矩的大小与飞行器外形参数、喷流参数,以及飞行马赫数、攻角、侧滑角等飞行状态参数有关[7]。由于返回舱外形参数和喷流参数为常值,故仅需考虑喷流力矩随飞行状态的变化关系,以多项式的形式表示为
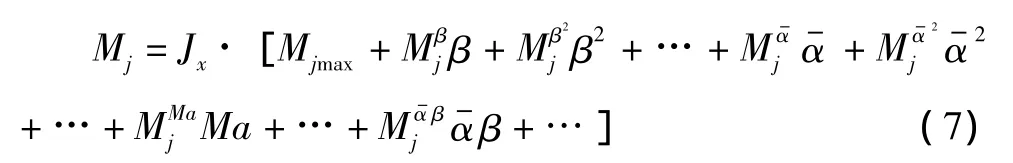
当状态参数为常值或变化很小时,喷流力矩峰值可以近似为一常数Mjmax,喷流力矩的时间历程曲线是一个等腰梯形(如图4)。定义喷流力矩的放大系数为:

式中,Mj0为无外流场条件下的喷流力矩,采用地面试验结果。
2.2 模型辨识方法
采用多项式形式的非线性模型,关于飞行状态变量是非线性的,但关于多项式系数却是线性的,对于线性模型,F统计检验是应用最广泛的模型假设检验。逐步回归法是采用F统计检验来考察预报因子与预报量相关性的显著性水平,逐项将影响显著的预报因子选入,并将相应的影响小的因子剔除,以建立最优数学模型的方法。采用复相关系数判断模型的优劣,复相关系数越接近于1,说明模型对预报量的拟合越好,模型越优。
根据飞行试验数据直接计算得到的力矩是气动力矩和喷流力矩的总和,它们通过流场耦合在一起,为了将二者区分开来,本文采取如下措施:选取一段飞行状态变化比较均匀,包含1~3次喷流控制的试验数据样本(如图1和图5),并将没有喷流发动机工作的时间段从样本中分离出来,组成一个子样本;利用子样本数据作为预报量,首先对气动力矩模型的候选因子进行筛选,得到气动力矩模型;对于有喷流发动机工作的情况,认为气动力矩模型是已知的,仅需对喷流力矩模型的候选因子进行筛选。由于所选样本数据中飞行状态参数变化比较均匀,并且由于喷流发动机的工作时间相对较短,分离出的子样本包含了所选样本数据的绝大部分,因此利用子样本得到的气动模型能够反映返回舱在整个样本时间段内的真实气动特性,在此基础上建立的喷流力矩模型也是可信的。以滚转控制喷流力矩模型为例,其候选因子为

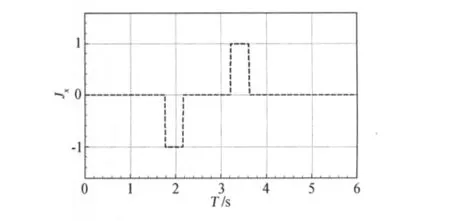
图5 喷流控制输入的时间历程Fig.5 Control input change with time
2.3 模型优选结果
选取某返回舱飞行试验的一段测量数据,取显著性水平 a=0.005,查 F 分布表得到 Fa=7.88。
表1给出了高超声速段选入滚转、偏航和俯仰力矩模型的因子,以及各因子的F统计检验值,同时还得到了各因子的拟合系数,作为参数估计的初值。选入气动力矩模型的为攻角、侧滑角和角速率的一阶项,上述参数的高阶项以及马赫数均未被入选,说明气动力矩模型是局部线性的,且在高超声速条件下可以忽略马赫数对气动力矩系数的影响。从表1还可以看出,只有滚转控制发动机开关机状态参数Jx入选了力矩模型,Jx与其它参数的组合参数未被入选,说明在一个辨识数据段内可以认为喷流力矩的峰值为一常数。另外,Jx也入选了偏航力矩模型,这是由于控制轴与体轴有一夹角,喷流力矩在偏航方向存在分量。
滚转、偏航和俯仰力矩系数模型的复相关系数均接近于1,说明力矩模型对试验数据拟合的很好,得到的模型是较优的。图6给出了力矩系数的试验值与模型拟合值的对比,可以看出,模型辨识得到的气动与控制力矩模型能够很好地拟合总力矩系数。
综上,高超声速段气动力矩模型和喷流力矩模型可以写成如下形式:

式中,Mjx,Mjy为喷流力矩的体轴系分量;φ为控制轴与体轴的夹角,为已知参数。

表1 入选力矩模型的因子Table 1 Selected factors of moment model
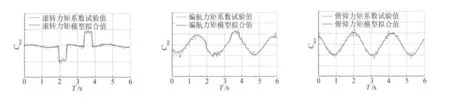
图6 力矩系数的试验值与模型拟合值Fig.6 Experimentation and model fitting of moment coefficient
3 气动参数估计
参数估计采用基于极大似然估计的输出误差方法,泛函极值的求解采用修正牛顿-拉夫逊方法,灵敏度的计算采用二阶中心差分方法。下面给出参数估计的数学模型。
3.1 状态方程组
状态方程为绕质心运动的动力学方程组。高度和速度为缓变量,直接采用重建后的轨道数据。
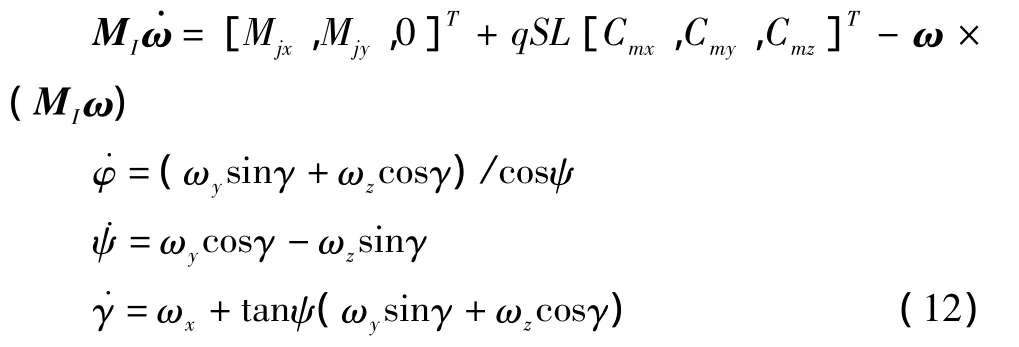
式中,φ,ψ,γ分别为俯仰角、偏航角和滚转角。
3.2 观测方程组
观测量取角速率和姿态角,观测方程为:
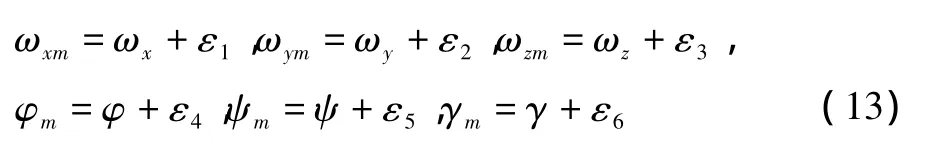
式中,下标“m”表示测量值;εi(i=1,2,…,6)为零均值随机噪声。
3.3 待估计参数
需要估计的参数为气动力矩模型与喷流力矩模型中的未知参数,即:
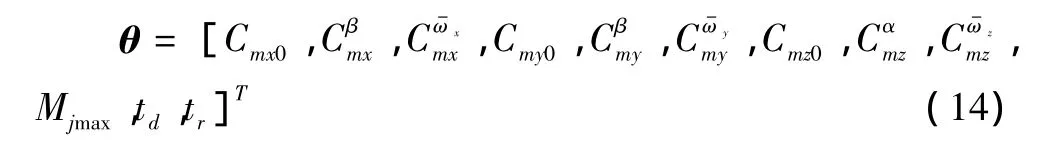
3.4 滞后时间估计
对于离散系统,滞后时间td决定了姿控发动机工作状态参数与观测量在时间上的对应关系,当滞后时间不是采样周期的整数倍时,发动机工作状态参数与观测量在时间上就无法一一对应。本文的解决办法是,在迭代计算的过程中,将滞后时间归整为采样周期的整数倍。
3.5 计算结果分析
以某返回舱为例,分别对高度在100km以上的一段飞行试验测量数据,以及60km以下,马赫数为12~16,喷流干扰较为明显的高超声速段飞行试验数据进行了辨识计算,得到了喷流控制力矩放大系数、滞后时间、过渡时间和气动力矩导数等主要气动与控制力矩参数。
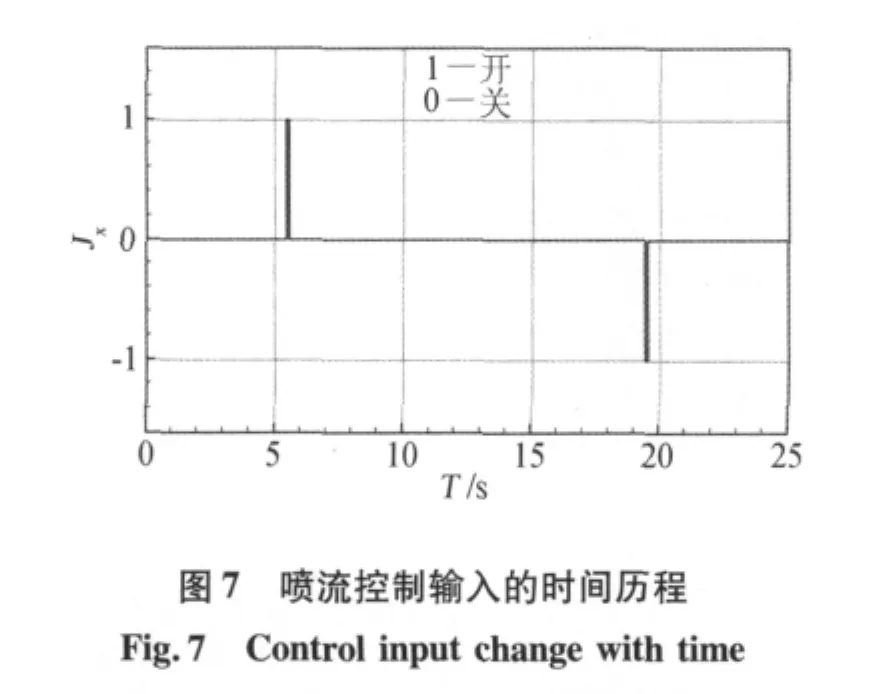
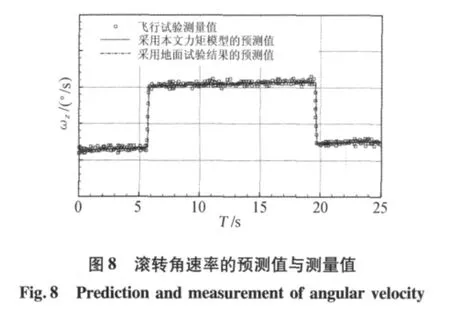
在100km以上的再入飞行段,返回舱飞行马赫数很高,选取的数据段内滚转控制发动机共有两次开机(如图7)。辨识得到的喷流控制力矩的放大系数为1,表明喷流产生的控制力矩与发动机地面试验结果完全一致,这是因为在这样的高度,大气非常稀薄,喷流干扰可以忽略。图8给出了观测量的预测值与测量值,可以看出,本文建立的气动与喷流控制力矩模型对观测量的预测值与测量值比较一致,说明辨识结果能够反映返回舱的气动与控制力矩特性。另外,由于高空动压很小,气动力矩不到控制力矩的千分之一,因此不可能采用气动力控制飞行器姿态,这种条件下喷流控制具有其独特优势。
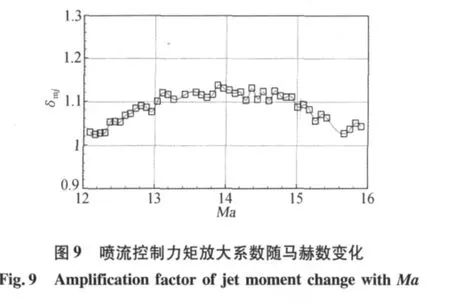
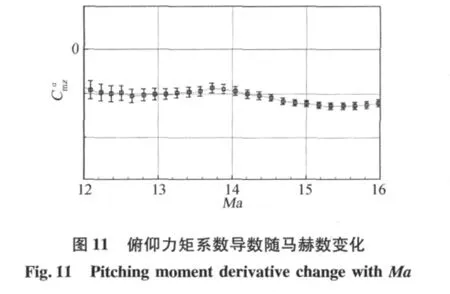
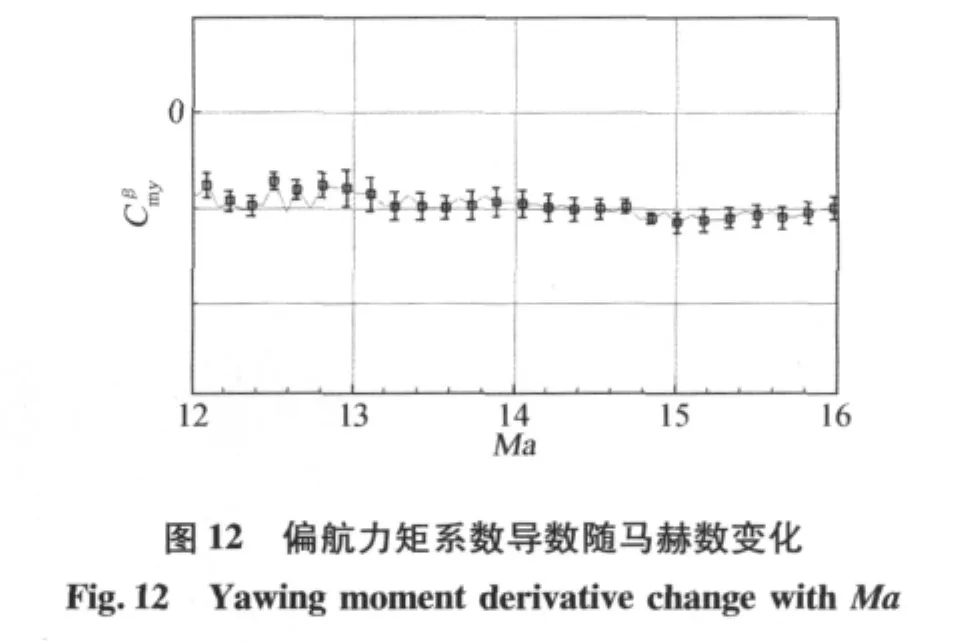
图9给出了60km以下高超声速段喷流控制力矩放大系数的估计结果,可见由于喷流干扰的存在,实际上放大了喷流控制力矩,这与有关文献的研究结论是一致的[3]。喷流力矩估计结果的不确定度取10倍的C-R界,其值小于2%。图10给出了滚转角速率的预测值与测量值,可以看出:直接采用喷流控制力矩地面试验结果时,由于未考虑喷流干扰效应,故不能很好地预测观测量;而采用本文建立的喷流力矩模型能够更好地预测观测量,说明辨识得到的喷流力矩能够真实反映姿控发动机的控制力矩特性,有利于更精确地控制返回舱的姿态运动。辨识同时还得到了气动力矩导数,以及其不确定度(如图11~12),为分析返回舱再入过程中的稳定性能和飞行性能提供了依据。

4 结束语
研究了喷流控制飞行器的气动参数辨识方法,并以飞船返回舱为例,利用飞行试验实测数据,通过模型辨识与参数估计,得到了返回舱再入过程中的喷流力矩滞后时间、喷流力矩放大系数和气动力矩导数等重要的气动参数。结果表明,在高超声速条件下喷流力矩的放大系数大于1,说明由于喷流干扰的存在,实际上对喷流控制力矩起到了放大作用,这与有关文献的研究结论是一致的。
本文建立的喷流力矩模型由于充分考虑了喷流力矩滞后、喷流力矩的动态变化过程、以及喷流力矩峰值随飞行状态的变化,因此能够真实反映姿控发动机的控制力矩特性,有利于更精确地控制返回舱的姿态运动。计算同时还得到了返回舱的气动静导数和动导数,以及上述参数的不确定度,为分析返回舱再入过程中的稳定性能和飞行性能提供了依据。
[1]蔡金狮,汪清.飞行器系统辨识学[M].国防工业出版社,2003.
[2]李素循.喷流控制飞行器姿态的物理问题[R].航天国防科学技术报告,2005.
[3]李素循.姿控发动机喷流对返回舱气动特性影响的风洞试验研究[A].载人航天工程气动研究文集[C].2004.
[4]KOUSUKE KIKUMOTO,et al.Sidejet aerodynamic interaction effect of the missile[R].AIAA98 -4347.
[5]ERNEST R HILLJE.Entry flight aerodynamics from apollo mission AS-202[R].NASA TN D-4185.
[6]ERNEST R HILLJE.Status of aerodynamic characteristics of the Apollo entry configuration[R].AIAA 68 -1143.
[7]ROGER R P.The aerodynamics of jet thruster control for supersonic/hypersonicendo-interceptors[R]. AIAA99 -0804.
