钝体边界层失稳特性分析

袁湘江，李 筠，田俊武，涂国华

(1.中国航天空气动力技术研究院，北京 100074;2.中国空气动力研究与发展中心，四川 绵阳 621000)

0 引言

传统的线性稳定性理论基于平行流假设，其适用范围必然受到一定限制。对于零压力梯度边界层，只有当考查范围较大时，非平行流的影响才比较明显。但在压力梯度较大时，即使在不大的范围内，流动的非平行性也会对流动的稳定性起重要影响。所以，对于复杂外形，边界层非平行性对稳定性的影响不能忽略。在非平行流的稳定性研究中，近十多年来发展起来的抛物化稳定性分析方法直接以发展的剪切层流动为研究对象，在揭示流动失稳机理以及转捩机理方面显示出了其更宽的适用性和更高的准确性［1－4］。已有的研究成果表明:它能像DNS一样刻画扰动的传播、失稳及非线性作用直到层流的崩溃阶段(以壁面摩擦力的突然增加来判断)，并与实验结果相一致。

美国、欧洲和日本等都开展了抛物化稳定性研究。在国内，南京航空航天大学的王伟志和唐登斌等人利用PSE方法对不可压缩流动的失稳问题进行了探讨，天津大学和中国空气动力研究与发展中心分别利用PSE方法对可压缩平板边界层的失稳与转捩问题进行了研究，中科院力学所则对抛物化稳定性的理论方面进行了讨论。但总的说来距离国际先进水平还有一定差距，未达到工程应用的要求。

为了推广PSE方法在航空航天方面的运用，本文开展了轴对称流动的抛物化稳定性研究，推导出了轴对称抛物化稳定性方程，以具有较强工程背景的高超音速球钝锥边界层为研究对象，通过线性稳定性方法得到起始位置处的扰动波形作为初始条件，利用PSE取得了有别于线性稳定性分析的稳定性初步分析结果。

1 轴对称抛物化稳定性方程

如图1所示，设x0－y0－z0为笛卡儿直角坐标系，x－y－z为曲线坐标系，R为子午线的曲率半径，rb为子午线上某点到对称轴的距离，那么拉梅系数可以表示为:

其中θ为x轴与对称轴的夹角。另外，对于带曲率的平板，可取H3=1。

图1 轴对称体以及坐标系Fig.1 Axisymmetric body and coordinate

在通常情况下，y的值是边界层厚度的量级，而R远远大于边界层厚度，同时认为R沿x方向的变化远小于R本身，于是有

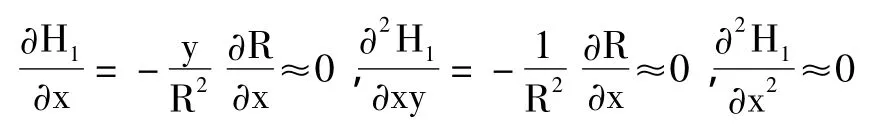
采用无穷远来流速度U∞，密度ρ∞，温度T∞，长度l0等为参考值，将N-S方程无量纲化，并定义雷诺数R=ρ∞U∞l0/μ∞。设流动可用基本流加上扰动量构成，如:

对于轴对称流动，有:

其中“*”表示任一基本流场量。

把(1)式代入可压N-S方程，考虑到(2)式，并省略非线性项后，可以得到线化的扰动方程:

其中 φ 由扰动量所组成，φ =［ρ，u，v，w，T］T，系数 Γ、A、B、C、D、Vxx等只与基本流场有关。

假设扰动量可表示为:

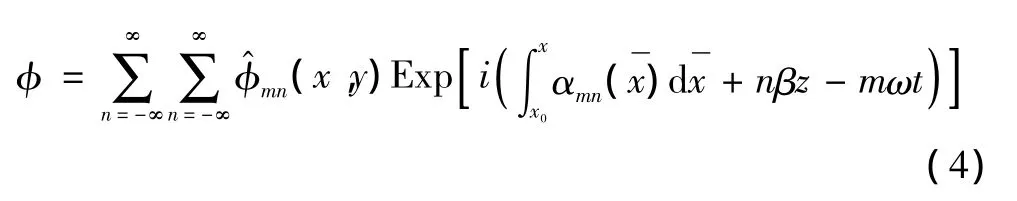
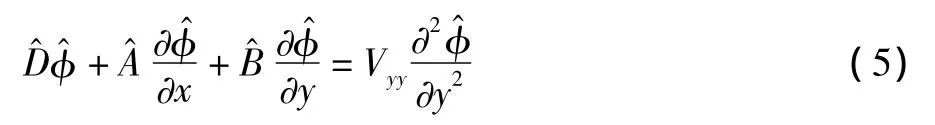
其中

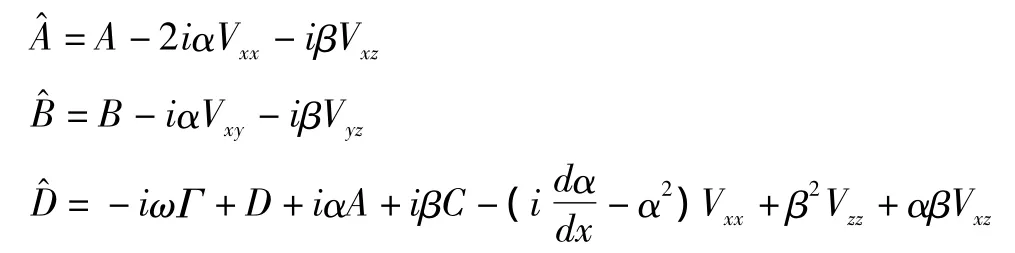
2 程序验证

为了检验程序的正确性，分别用不同方法计算了平板边界层扰动波的增长因子和考查了流向曲率对稳定性的影响。当曲率半径R趋向于无穷大时，曲面演变成平面。本文考虑Ma=4.5的平板问题，在当地雷诺数Rx=1500(参考长度为的地方引入T-S波，分别利用LST、PSE和DNS求解该T-S波的增长因子N沿流向的发展。图2(a)给出了在不同流向位置处不同方法获得的N值比较，图2(b)给出了在不同流向位置处DNS与PSE方法获得的波形比较，结果是吻合的。从而验证了程序的正确性。

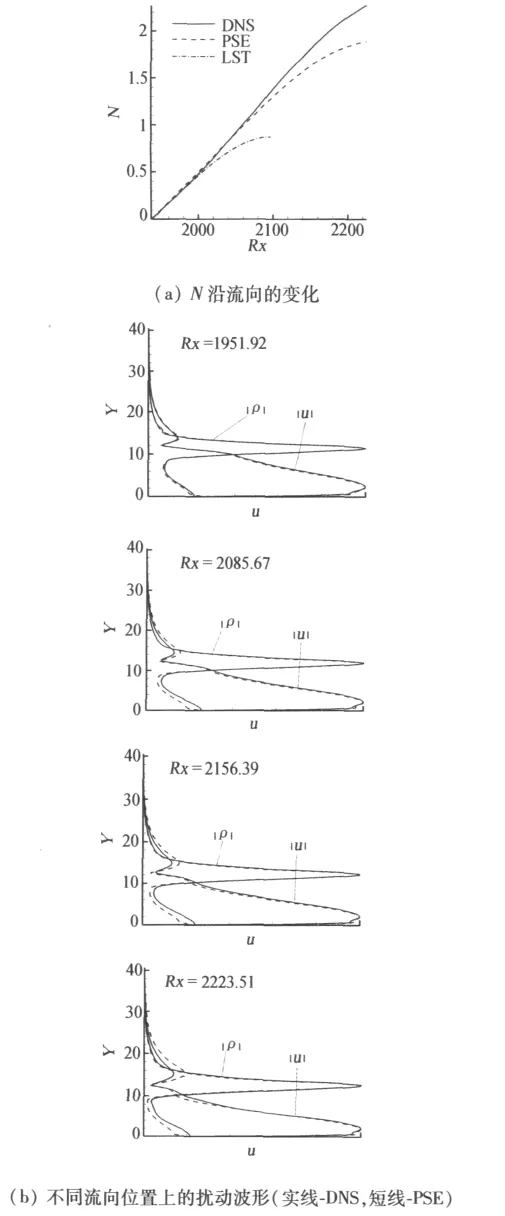
图2 不同方法获得的N与波形在不同流向位置的比较Fig.2 Comparing N-factor and disturbance shapes acquired by different methods on different streamwise positions

为检验本文PSE方法研究曲率对稳定性影响的正确性，图3给出了不同流向曲率半径下扰动增长因子沿流向的增长情况。其中正的曲率半径表示凸外形，负的曲率半径表示凹外形。从图中可以明显看出，随着曲率减小(R的绝对值增大)，扰动增长情况向无曲率的平板靠近;正曲率具有增强稳定性的作用，曲率越大扰动增长越慢;负曲率具有失稳作用，曲率的绝对值越大扰动增长越快。这与袁湘江等人［5］采用线性稳定性(LST)的分析结果一致，与Christian［9］等人采用其他分析方法所得的结果也一致，还与Malik＆Balakumar［10］的不可压LST结果一致。文献［11］采用Malik＆Poll方法研究了曲率对稳定性的影响，也得出正曲率具有稳定性作用，负曲率具有失稳作用。

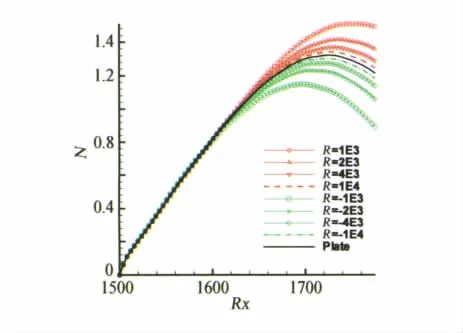
图3 增长因子随Rx的变化Fig.3 Increasing factor N as a function of Rx

3 球钝锥稳定性分析

由于根据线性稳定性理论分析，钝体头部流场中的边界层总是稳定的，利用这种方法对钝体进行的转捩预测，其转捩位置都在远离头部的锥身上。但Widhopf和Hall的地面实验表明，在某些条件下，转捩位置是在钝锥的头部，并不是在锥身。这一点也可以从美国的NRV、回收的Gemini返回舱以及我国神州一号返回舱的烧蚀外形上得到了证实。近年来，人们经过长期研究逐渐认识到，钝体端头边界层的失稳机制可能与边界层的非平行性以及流向速度变化有关，也可能其转捩机理根本不是自然转捩，即跃过线性发展阶段直接转捩，即:“Bypass”转捩。鉴于这些考虑，本文利用上述轴对称抛物化稳定性方程，对钝锥端头边界层进行稳定性分析，并与线性稳定性理论的分析结果进行比较。初始流场的状态参数为:M=6.0，Re=2 ×106，T∞=100K，TW=300K。计算外形是5°钝锥，基本流场的计算区域和网格系统见图4。为提高效率，在计算时，采用轴对称NS方程和激波装配技术。计算网格点为241×251。

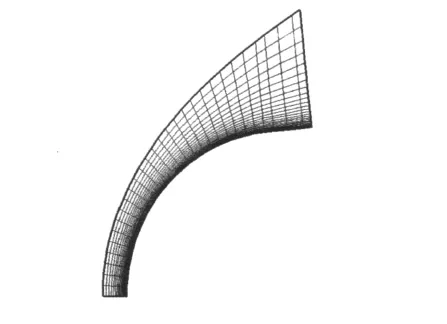
图4 基本流场的计算区域和网格系统Fig.4 Computational zone of base flow and mesh

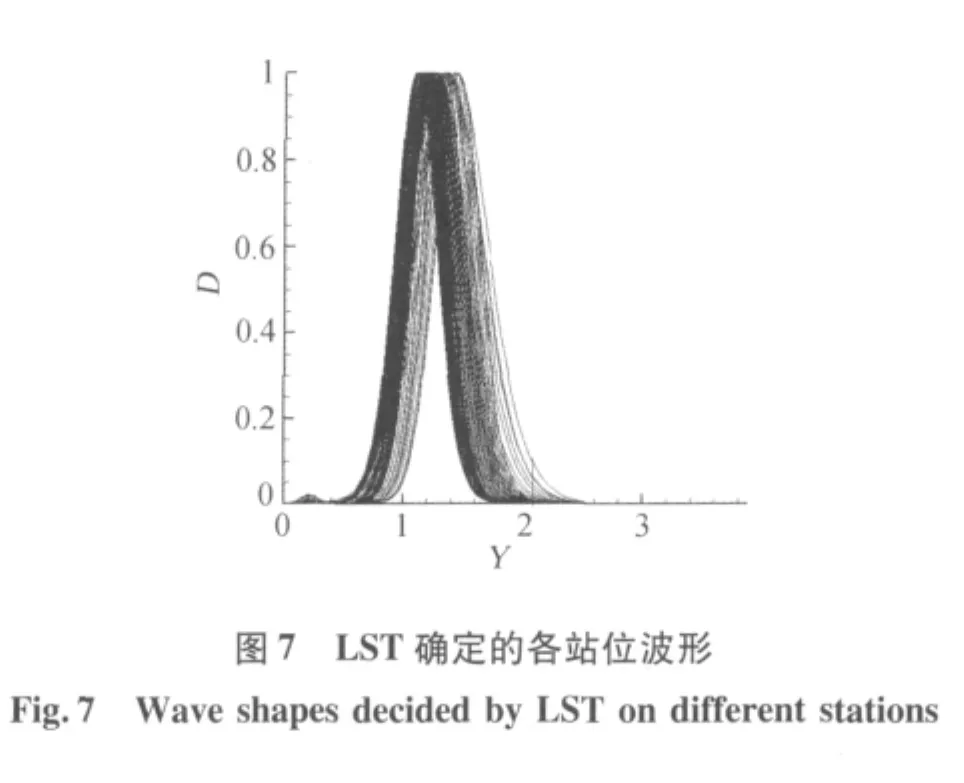
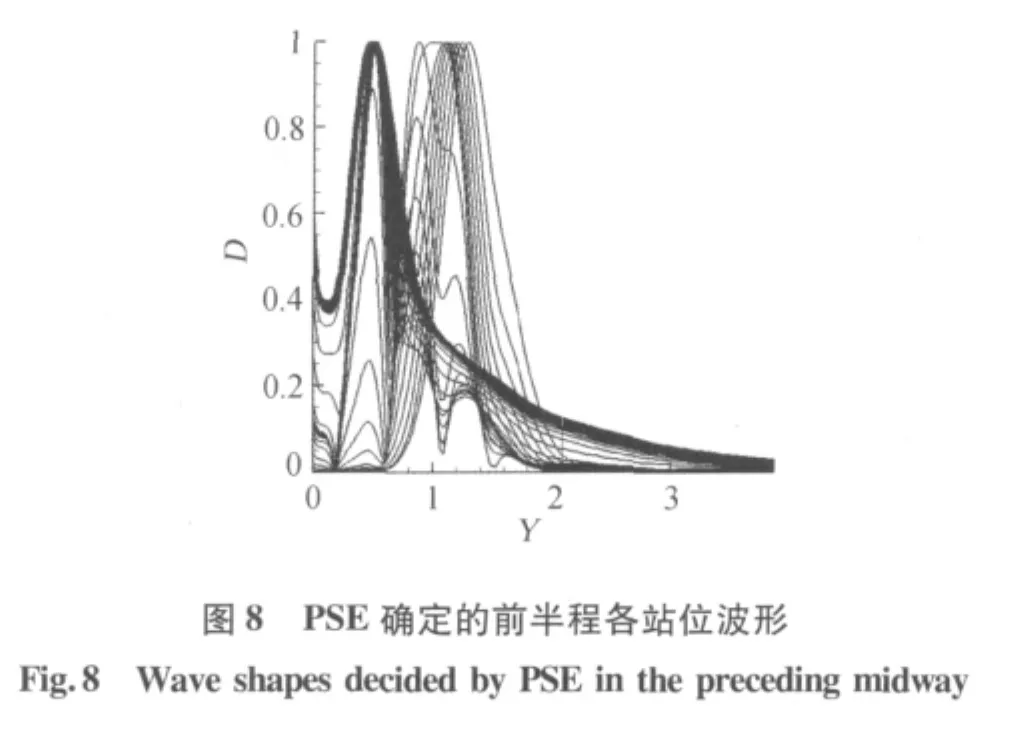
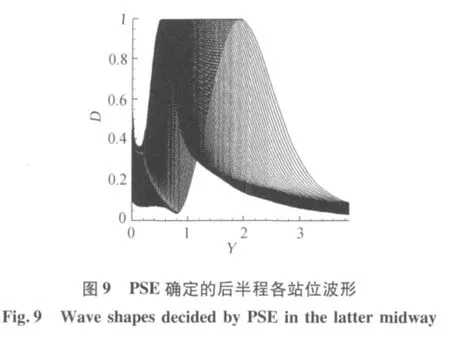
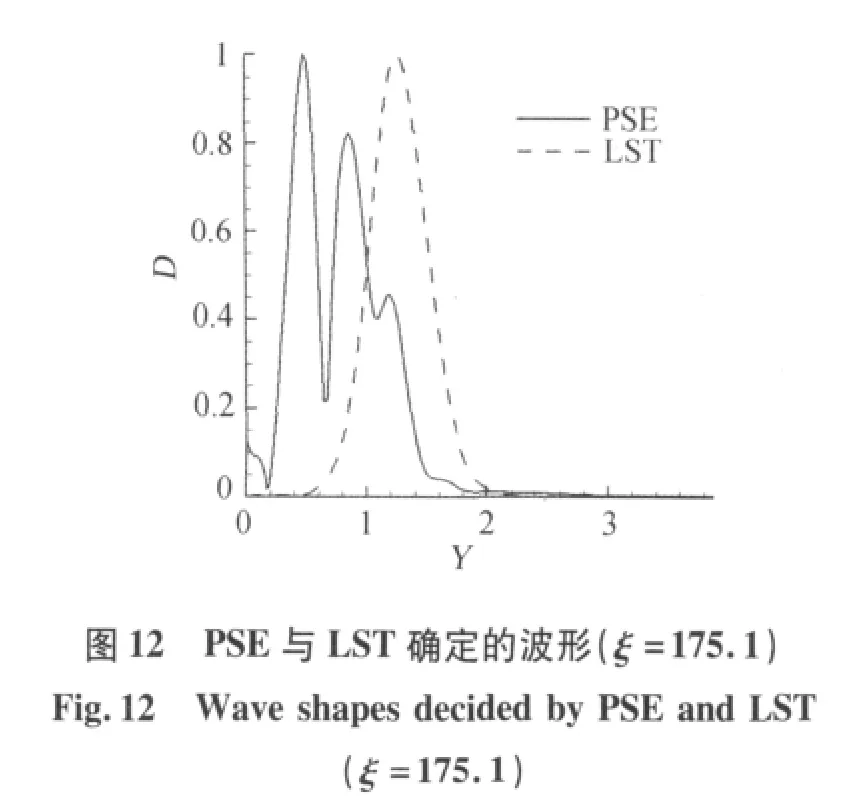
在稳定性分析中，以球钝锥的驻点作为坐标原点，球钝锥的表面弧长作为流向坐标。为了方便对两种稳定性理论的分析结果进行比对，取与体轴夹角为18°处，为扰动波的入口，入口处的扰动波由LST确定。图5、图6分别表示根据LST得到的放大因子与根据PSE得到的放大因子。由图可知，根据LST，扰动始终衰减;而根据PSE，扰动波在传播一段距离后，出现增长。可见对于球钝锥边界层非平行性以及流向速度变化对扰动增长与衰减特性有较大影响。图7表示根据LST确定的在流向各站位的规一化波形比较，可见各站位波形峰值点沿流动方向逐渐向边界层外缘移动，除此之外，波形几乎没有变化。图8、图9分别表示根据PSE确定的在流向前半程与后半程各站位的规一化波形比较，可见前半程各站位波形变化较大，与根据LST确定的前半程波形变化不同，根据LST确定的前半程波形一开始波形峰值点沿流动方向向壁面方向移动，壁面附近出现第二峰值，并且第二峰值逐渐增长到超过第一峰值后，第二峰值点逐渐向边界层外缘移动。而后半程波形沿流动方向变化较小，只看到第二峰值点逐渐向边界层外缘移动。图10到图15为波传播前半程几个站位由LST确定的规一化波形与PSE确定的对应站位规一化波形的比较。由图可知，在扰动增长特性变化前，LST确定的波形与PSE确定的波形基本相似，而在扰动增长特性变化点附近PSE确定的波形变化较大，开始出现多峰值。在扰动增长特性变化后，扰动波模态改变，波形相对稳定。

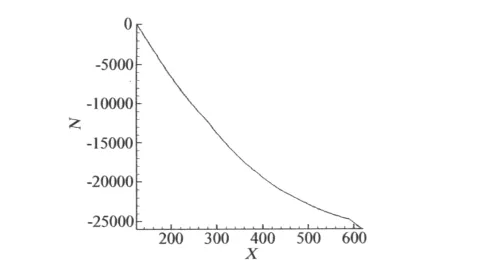
图5 LST确定的增长因子Fig.5 Increasing factor N decided by LST

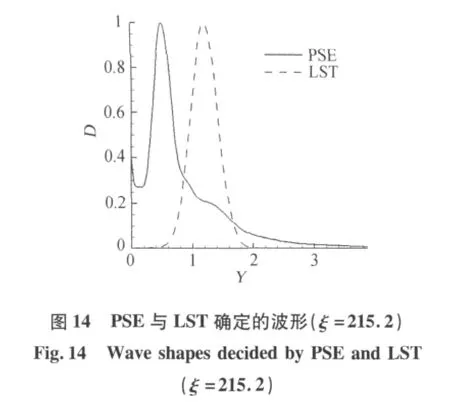
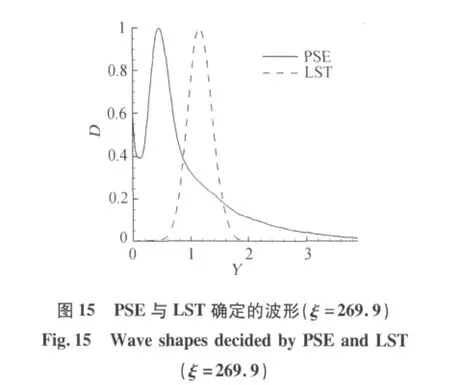
4 结论

本文推导了平板/轴对称抛物化稳定性方程，并通过与LST和DNS的结果比较验证了程序的正确性，并系统研究了超音速钝体边界层的失稳机制，结果表明:1)随着扰动波向下游的传播，曲率对扰动波的影响增大，正曲率起失稳的作用，负曲率起稳定的作用;2)流动的非平行性以及流向速度变化对扰动增长与衰减特性有较大影响，在一定条件下，可以改变扰动的增减性质;3)流动的非平行性以及流向速度变化对波形的有较大影响，尤其扰动波在增减性质发生变化时，波形变化较大;4)球钝锥边界层中的失稳扰动波是TS波通过演化形成的。线性理论不能反映TS波的演化，因此，无论在什么地方都找不到失稳的解;5)在球钝锥边界层中叠加TS波时，应有足够大的幅值，否则将在开始阶段被完全衰减。

［1］HERBERT T.Parabolized stability equations［J］.Annual Review of Fluid Mechanics，1997，29:245-283.

［2］HU S，ZHONG X.Nonparallel stability analysis of compressible boundary layer using 3-D PSE［R］.AIAA 99 －0813，1999.

［3］CHANG C，MALIK M R.Non-parallel stability of compressible boundary layers［R］.AIAA 93 －2912，1993.

［4］LI F，MALIK M R.Spectral analysis of parabolized stability equations［J］.Computers ＆ Fluids，1997，26(3):279-297.

［5］袁湘江，周恒.考虑流向曲率和压力梯度的可压缩边界层稳定性分析［J］.空气动力学学报，1998，16(3):276－281.

［6］CHRISTIAN M，STEPHAN B，MARC L，et al.Curvature and nonparallel effects in 3-D compressible transition analysis［R］.AIAA97－0824，1997.

［7］MALIK M R，BALAKUMAR P.Linear stability of three-dimensional boundary layers-effects of curvature and non-parallelism［R］.AIAA 93－0079，1993.

［8］LI M J，GAO Z.Analysis and application of ellipticity of stability equations on fluid mechanics［J］.Applied Mathematics and Mechanics(English Edition)，2003，24(11):1334－1341.

［9］CEBECI T，CHEN H H，KAUPS K.Further consideration of the effect of curvature on the stability of three-dimensional flows［J］.Computers＆ Fluids，1992，21(4):491 －502.

［10］涂国华，袁湘江.超声速平板边界层流动的二维抛物化稳定性研究［A］.中国第一届近代空气动力学与气动热力学会议［C］.四川绵阳:国防工业出版社，2006.809－813.