k个矩阵的核子空间的和的维数
2011-11-02左可正
左可正, 谢 涛
(湖北师范学院数学与统计学院,湖北黄石 435002)
k个矩阵的核子空间的和的维数
左可正, 谢 涛
(湖北师范学院数学与统计学院,湖北黄石 435002)
利用齐次线性方程组的解的表达式及分块矩阵的一个秩等式,得出了k个矩阵的核子空间的和的维数的一个公式,它推广了维数公式.并给出了这个公式的几个应用.
核子空间;值域;秩;维数
1 引言及预备引理
本文恒设F是特征为0的域.用Fm×n表示F上的所有m×n矩阵组成的集合,Fn表示F上的n维列线性空间.设A∈Fm×n,用r(A),R(A),N(A)和A-分别表示A的秩,值域,核子空间和广义逆(AA-A=A).用I n表示n级的单位矩阵.用F[x]表示域F上的x的一元多项式环.
在线性代数中,有一个下面众所周知的维数公式:
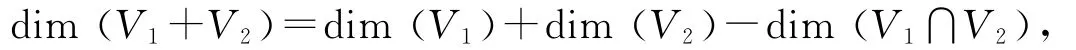
其中V1,V2是域F上的有限维线性空间V的两个子空间.
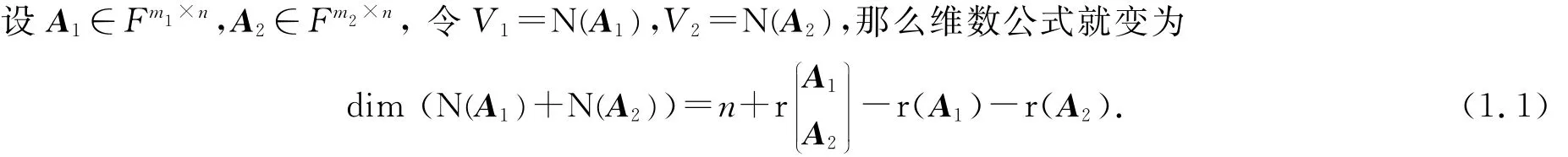
本文将公式(1.1)进行了推广,得出了

其中A1∈Fm1×n,A2∈Fm2×n,…,A k∈Fmk×n.并给出了这个公式的几个应用.
为了证明(1.2)式,需要下面的引理1与引理2.

为了给出公式(1.2)的几个应用,我们还需要下面的引理.这个引理的结论,本身给出了两个有趣的秩等式.
引理3设
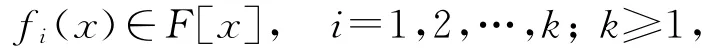
f1(x),f2(x),…,f k(x)是两两互质的,A∈Fn×n,那么

证 先用数学归纳法证明(1.5)式.
当k=2时,因为f1(x),f2(x)是互质的,那么存在u(x),v(x)∈F[x],使得
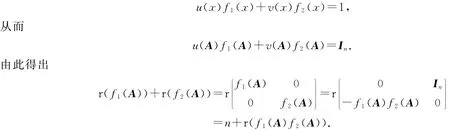
归纳假设k-1时(1.5)式成立,当为k时.由归纳假设及f1(x)f2(x)…f k-1(x)与f k(x)互质,我们得出
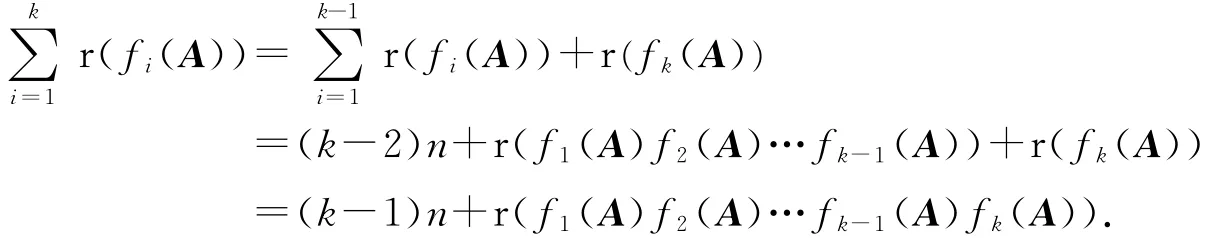
由数学归纳法,(1.5)式成立.
下面用数学归纳法证明(1.6)式.
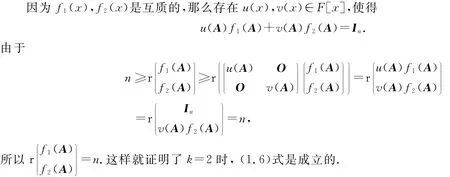
归纳假设k-1时(1.6)式成立.当为k时,因为f1(x),f2(x),…,f k(x)是两两互质的,那么f1(x)与f2(x)f3(x)…f k(x)是互质的.这样存在u1(x),v1(x)∈F[x],使得
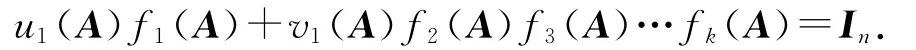
由于

2 主要结果及其应用



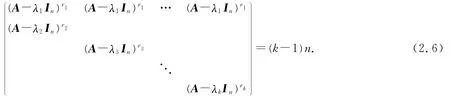
由(2.5)式和(2.6)式及推论2,得出
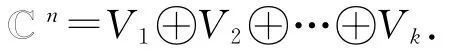
下面利用推论2及引理3,来给出两个高等代数考研试题的证明.
例1(2007年大连理工大学高等代数考研试题) 设V1,V2是x1+x2+…+x n=0和x i-x i+1=0,i=1,2,…,n-1的解空间.证明:
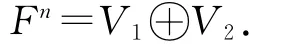


[1]Ben-Israel A,Greville T N G.Generalized inverses:Theory and Applications[M].2nd.New York:Springer,2003.
[2]Marsaglia G,Styan G P H.Equalities and inequalities for ranks of matrices[J],Linear and Multilinear Algebra,1974(2):269-292.
[3]北京大学数学系几何与代数教研室.高等代数[M].北京:高等教肓出版社,2003.
The Dimension of the Sun of Nullspaces of k Matrices
ZUOKe-zheng,XIETao
(Department of Math of Hubei Normal University,Huangshi,Hubei,435002,China)
By using the expression of the solution of some homogeneous linear equations and a rank equlity of partitioned matrices,a formular of the dimension of the sun of nullspaces ofkmatrices is obtained,which generalized dimension formular,and some applications of the formular are given.
nullspace;range;rank;dimension
O151.21
A
1672-1454(2011)04-0128-05
2008-12-04
湖北师范学院教研项目(21)
