对称熵损失下一类指数分布族的Bayes估计

史晓明，蔡春娟(吉林师范大学数学学院，吉林四平136000)

对称熵损失下一类指数分布族的Bayes估计

史晓明，蔡春娟
(吉林师范大学数学学院，吉林四平136000)

文中研究了在对称熵损失函数下，一类指数分布族参数的Bayes估计及其可容许性，并讨论了一类形式cT+d的可容许性.

对称熵损失函数;Bayes估计;可容许性

1 引言

意义下考虑参数θ的估计，其中δ是θ的判决空间中的一个估计，由数学分析知识知道这个损失函数L(θ，δ)关于δ是严格凸函数，并且在δ=θ处取得唯一的最小值.

2 可靠度θ的Bayes估计

我们讨论参数θ的Bayes估计，对任意先验分布，θ的Bayes估计

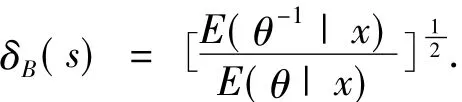
定理1在损失函数(1)下，对于任何先验分布，θ的Bayes估计为

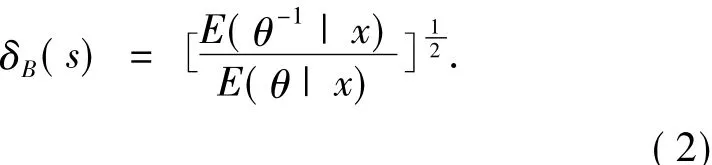
这里的x=(x1，x2，…，xn)，若δB(s)的Bayes风险有限，则它还是唯一的Bayes估计.

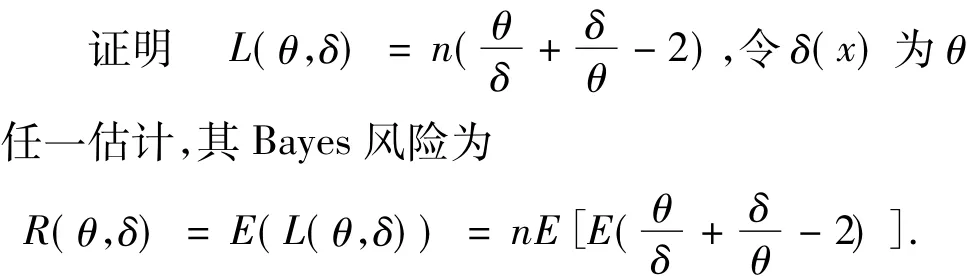
上式的左端表示关于θ和的联合分布取期望，欲使R(θ，δ)达到最小，只须后验风险达到最小，由于E(+－2)=·E(θ|x)+δ·E(θ－1|x)－

下面以定理的形式给出的θ的精确Bayes估计.

定理2θ的先验分布Γ(α，λ)取在损失函数(1)下，其分布参数θ的Bayes估计为

引理1在给定的Bayes决策问题中，假如对给定的先验分布π(θ)，θ的Bayes估计是唯一的，则它是容许估计［3］.

由于对称损失函数(1)是严格凸函数，其Bayes估计必是唯一的，由引理1可知，Bayes估计δB(x)亦是可容许估计.

3 估计量cT+d的容许性

可以看出，在适当的逆伽玛分布先验分布下，参数θ的估计量都有形式cT+d，而形如cT+d的这类估计的可容许性与c和d的取值有关.下面对c和d的不同取值情况分别进行讨论.

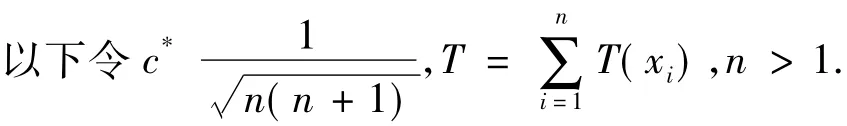
定理3当0cc*，d＞0估计量cT+d是可容许的.

证明在对称熵损失函数下，我们证明了θ有唯一的Bayes解:

当c=0，d＞0时，估计量为常值d，若此时估计量不可容许，必存在某一个估计量δ1(X)优于d，即0R(θ，δ1(X))R(θ，d)，对某些θ不等号严格成立.

当θ=d时，有0R(θ，δ1(x))R(θ，d)=0，即R(θ，δ1(X))=0，由损失函数的非负性可知L(d，δ1(X))=0，故δ1(X)=da.e，所以，当c=0，d＞0时，估计量cT+d是可容许.

［1］韦博成.参数统计教程［M］.北京:高等教育出版社，2006.

［2］茆诗松，王静龙，濮小龙.高等数理统计［M］.北京:高等教育出版社，2006.

［3］茆诗松.贝叶斯统计［M］.北京:中国统计出版社，1999.

［4］李文东，张强，张建军.一类指数分布族的渐进最优和可容许的经验Bayes估计［J］.孝感学院学报，2006，26(3).

(责任编辑:王宏志)

Abstract:In the paper，we study the Bayesian estimation of the parameters on a class of Exponential Distribution Family under Symmetric Entropy Loss Function.We prove that the Bayesian estimation is admissible，and discuss the admissibility of a class of cT+d form.

Key words:symmetric entropy loss function;Bayesian estimation;admissibility

Bayes Estimation on a Class of Exponential Distribution Fam ily under Symmetric Entropy Loss Function

SHIXiao－ming，CAIChun－juan
(School of Mathematics，Jilin Normal University，Siping，Jilin 136000，China)

O212.8

A

1008－7974(2011)04－0015－02

2011－01－06

史晓明(1987－)，女，吉林长春人，吉林师范大学在读硕士研究生.