指数型分布粗糙地面电磁散射的FDTD研究

朱小敏,任新成,郭立新

(1.西安电子科技大学 理学院,陕西 西安 710071;2.延安大学 物理与电子信息学院,陕西 延安 716000)

0 引言

近年来,随机粗糙表面电磁散射的理论和实验研究取得了一系列重要进展。该类问题的应用广泛,如微波遥感中地面目标分类、地面背景中目标检测及遥感数据判读等均受到地面散射特性的影响。随机粗糙面散射理论可分为近似解析方法与数值方法两大类。近似解析法根据粗糙表面的粗糙程度,采用不同的物理近似获得散射场或散射截面的近似解,实现较简单,但因采用了各种物理近似,故均有一定的适用范围。数值法中的FDTD首先由YEE于1966年提出,经40多年的发展已成为一种成熟的数值方法[1-9]。针对地面散射,文献[10]用辐射传输理论(RT)研究了道路系统体散射特性,用积分方程方法(IEM)分析了地面表面散射特性;文献[11]用基尔霍夫近似和几何光学方法计算了路面背景中目标的电磁散射特性;文献[12]用积分方程方法计算了指数型粗糙地面的后向散射系数;文献[13]用FDTD方法计算了地下目标的雷达散射截面。其中,文献[10、11]中道路系统均为水泥沥青路面,采用的方法为近似解析方法。文献[13]提出了在FDTD中强加入射源的一种新方法,但该法仅对分界面为平面时有效,对粗糙地面问题该加源方法存在较大困难。

本文基于指数型随机粗糙地面的模拟方法和土壤介电常数计算Wang-Schmugge模型,用FDTD对指数型分布粗糙地面电磁散射特性进行了研究,数值计算了指数型分布粗糙地面的双站散射系数,讨论了粗糙面高度起伏均方根、相关长度、土壤湿度和入射波波长对散射系数的影响。

1 指数型粗糙地面模拟与土壤介电常数

1.1 指数型粗糙地面模拟

实际自然背景和人造表面均可视作二维粗糙表面模型。在各种二维粗糙表面模型中,当模型仅沿坐标系的一个方向发生变化,在另一个方向几乎不变时,这类二维粗糙表面可简化成一维粗糙表面模型。尽管一维粗糙表面是最简单的粗糙表面模型,但研究一维粗糙表面模型的电磁散射特性仍有重要的实际意义和广泛的应用价值。

一维随机粗糙面可用蒙特卡罗(MC)法模拟生成[14]。粗糙表面被认为是由大量的谐波叠加而成,谐波的振幅是独立的高斯随机变量,其方差正比于特定波数的功率谱S(kj),由函数

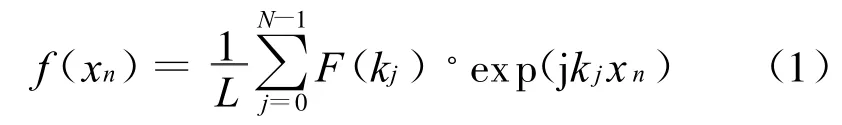
生成长度为L的一维粗糙表面样本。此处：xn=nΔx为粗糙表面上第n个离散点(n=1,2,…,N);Δx为粗糙面采样间隔;kj为离散波数,且kj=2πj/L;j为虚数单位;F(kj)为f(xn)的空间傅里叶变换,定义为

其中：S(kj)为粗糙表面的功率谱密度;N(0,1)表示均值为0、方差为1的高斯随机变量。当j＞N/2时,F(kj)满足共轭对称关系F(kj)=F*(kN-j)。这样可保证进行傅里叶逆变换后所得粗糙表面的轮廓f(xn)为实数。

指数型分布粗糙表面的功率谱密度为

式中：δ为粗糙面高度起伏均方根;l为相关长度;k为空间波数。

处理粗糙面下方土壤模型的方式有多种,最简单的是将土壤作为各向同性均匀介质,如考虑土壤湿度随深度的变化,可将土壤视作分层介质。同样当土壤覆盖冰层或雪层时也常用分层介质模型处理。

1.2 土壤介电常数Wang-Schmugge模型

微波波段土壤的介电常数对雷达回波的影响很大,介电常数越大,反射雷达波束的作用越强,透射作用越小。一般来说,土壤的介电常数主要受入射频率f、土壤湿度mv、土壤表面温度T和土壤类型等因素的影响。WANG,SCHMUGGE建立了一种四成分模型[15]。设土壤的沙土含量为S,黏土含量为C,则土壤的湿度压缩点

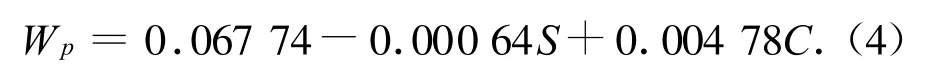
则临界体湿度

设土壤中岩石密度为ρr,干土壤密度为ρb,则土壤的积孔率

一般,ρr=2.6 g/cm3,而

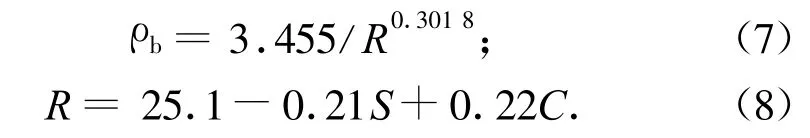
当mv≤mt时,土壤等效介电常数

式中：εa为空气的介电常数,且εa=1.0;εr为岩石的介电常数,且εr=5.0-j0.1;

此处：εi为冰的介电常数,且εi=3.2-j0.1;

当mv＞mt时,

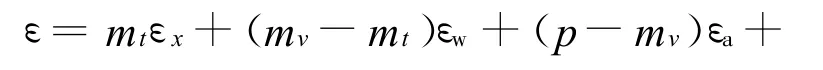
式中：

不同土壤类型沙土和黏土含量见表1。

表1 不同土壤类型沙土和黏土含量Tab.1 Sand and clay content of different types soil

2 FDTD方法

一维随机粗糙面电磁散射几何关系如图1所示。图中：粗糙面上方为自由空间;下方为各向同性均匀介质。粗糙面电磁散射计算的FDTD模型如图2所示。图中：总场边界为平面;下方为总场区;上方为散射场区。入射波通过设置在总场边界上的等效电磁流引入,散射数据存储边界处于散射场区,由等效原理可求得远区散射场。

图1 一维粗糙面散射几何示意Fig.1 Geometry of scattering from 1 D rough surface

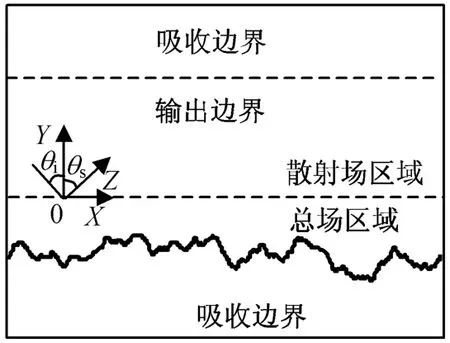
图2 粗糙面散射FDTD模型Fig.2 FDTD model of scattering from rough surface

2.1 二维麦克斯韦方程FDTD差分公式

对二维麦克斯韦方程,TM波仅有Ez,Hx,Hy分量,TE波仅有Hz,Ex,Ey分量。以TM波为例,FDTD差分公式为

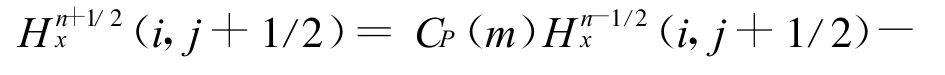
式中：Δx,Δy分别为FDTD区域x、y向的离散网格宽度,计算中Yee元胞采用正方形,即Δx=Δy;系数

此处：Δt为间离散间隔,需满足Courant稳定性条件,本文取cΔt=Δx/2;c为真空中光速;ε为介质介电系数;μ为磁导系数;σ为电导率;σm为导磁率[1-3]。CA,CP,CQ中标号m的取值与式(17)～(19)左端场分量节点的空间位置相同。根据TE波与TM波间的对耦关系：ε→μ,μ→ε,σ→σm,σm→σ,E→H,H→-E,可得TE波的FDTD差分公式。

2.2 入射波引入

根据等效原理在总场边界设置等效电磁流,可在总场区引进入射波,而在散射场区无入射波。假设入射角为θi;波数为ku;为坐标轴方向单位矢量,则

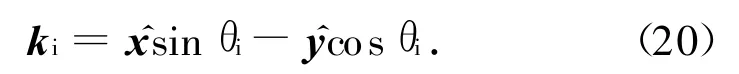
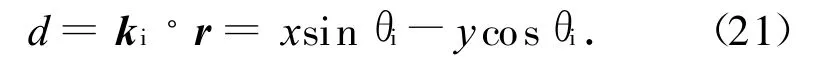
内插确定距离d的入射波为

式中：floor表示向下取整。总场边界上点r的入射场值

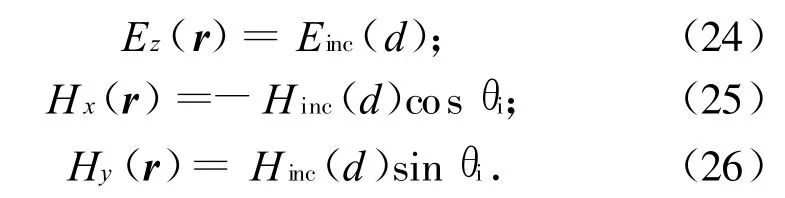
为消除截断边界处场值突变产生的人为反射,在入射平面波附加平滑的窗函数,常用高斯窗函数

式中：x0,y0为总场边界的中心点位置,本文取x0=0,y0=0;选择的g应使窗函数在总场边界边缘处下降为中心点处值的10-3。设ρm为中心到边缘最小距离,

则有

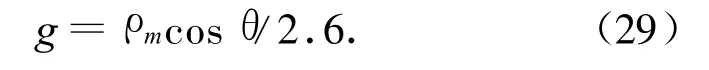
2.3 吸收边界条件

因受限于计算机的容量,FDTD计算只能在有限区域进行。为能模拟开域电磁散射过程,在计算区域的截断边界处须给出吸收边界条件[2、4]。二阶Mur吸收边界条件的FDTD差分公式为

a)左侧截断边界

b)下侧截断边界

右侧与上方截断边界差分公式可分别仿照式(30)、(31)写出。

2.4 近-远场外推

根据惠更斯等效原理,在散射体周围引入虚拟界面A,如图3所示。设面A外为真空,如保持界面A处场的切向分量不变,而令面A内的场为零,则根据惟一性定理,图3中原问题与等效问题在面A外的场有相同的分布。

图3 等效原理Fig.3 Principle of equal effects

FDTD计算中,在计算达到稳态后提取输出边界上场的幅值和相位,用时谐场外推公式进行外推,则有

式中：k为入射波数;Z为波阻抗;φ为散射波与x轴夹角,且φ=90°-θs。此处：θs为散射角。电流矩和磁流矩分量可分别表示为

式中：jEF为输出边界节点坐标。

由式(32)～(34)可得远区散射场Es,远区雷达散射截面

远区散射系数

3 数值计算

用本文方法数值计算了不同θs时指数型分布粗糙地面双站散射系数,讨论了粗糙面粗糙度参数高度均方根h与相关长度l、入射波长λ,以及mv,θi等参数对散射系数的影响。数值计算中,取粗糙面的抽样长度为50个波长,在数值离散时每个波长取20个点。为减小误差,选用100个随机粗糙面计算,取双站散射系数的统计平均值。

在λ=0.03 m,θi=30°,l=1.5λ,ε=8.331 6-j3.258 6(即mv=0.2)条件下,粗糙地面不同h对双站散射系数的影响如图4所示。由图可知：σ在镜反射方向(θs=30°)和后向散射方向(θs=-30°)均存在极大值。总体而言,σ随h增大而增大,但镜反射方向和后向散射的峰值随h的变化并不明显。另外,当h较小时,θs在30°～70°和-30°～-70°范围内散射系数起伏较大,存在若干明显的极值,但随着h的增大,这些起伏逐渐减小,极值并不明显。

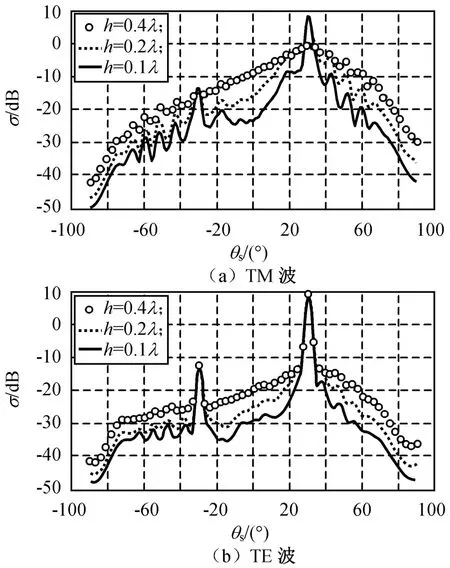
图4 粗糙地面均方根对散射系数的影响Fig.4 Influence of root mean squareof rough land surface on scattering coefficient

在λ=0.03 m,θi=30°,h=0.5λ,mv=0.2条件下,不同l对双站散射系数的影响如图5所示。由图可知：l对双站散射系数的影响较复杂,无明显的单调变化规律。比较TM、TE波可发现：θs在20°～70°和-20°～-70°范围内,TE波散射系数较TM波小5～15 d B,TE波的镜向和后向散射幅度基本不变,TM波的镜向散射幅度随l增大而略减小。

图5 粗糙地面相关长度对散射系数的影响Fig.5 Influence of correlation length of rough land surfaceon scattering coefficient

图6 土壤湿度对散射截面的影响Fig.6 Influenceof moisture capacity of soil on scattering coefficient

在λ=0.03 m,θi=30°,h=0.2λ,l=1.5λ条件下,不同mv对双站散射系数的影响如图6所示。湿度的变化实质是土壤介电常数的变化。利用式(9)、(15),若土壤类型为沙壤土,土壤表面温度为15℃,计算不同湿度时土壤的介电常数,通过FDTD计算可得土壤湿度对双站散射系数的影响曲线。由图可知：散射系数随湿度增加而增大,TM波镜向散射与后向散射的幅值随湿度增加而增大,TE波镜向散射与后向散射的幅值基本不变。

在θi=30°,h=6 mm,l=45 mm的条件下,mv=0.2、εr变化和εr=3.75-j1.06、mv变化时不同λ对双站散射系数的影响分别如图7、8所示。由图7可知：当湿度相同时,TM波镜向和后向散射幅值随入射波长减小而变小;TE波的镜向和后向散射幅值基本不随波长而变,另外除镜向外,当θs＞-20°时,λ越小,双站RCS就越大。由图8可知：当εr相同时,镜向和后向散射的变化规律与图7相似,TM、TE波均显示当θs＞-20°时,除镜向外散射系数随波长减小而增大。

图7 土壤湿度相同时入射波长对散射截面的影响Fig.7 Influence of length of incidence wave on scattering coef ficient with the same soil moisture

图8 介电常数相同时入射波长对散射截面的影响Fig.8 Influence of length of incidencewave on scattering coefficient with thesame permittivity

4 结束语

本文用FDTD方法研究了指数型分布粗糙地面的电磁散射特性,分析了双站散射系数随粗糙地面高度起伏均方根、相关长度、土壤湿度,以及入射波长等参数变化的规律。数值计算结果表明：双站散射系数随粗糙地面高度起伏均方根、相关长度、土壤湿度和入射波长等参数变化的规律非常复杂。本文采用指数型粗糙面模拟实际的粗糙地面,用FDTD研究了该粗糙面的电磁散射问题,且仅限于一维的情形,计算结果有待于实验验证。对分形地面及二维粗糙地面的电磁散射等其他类型的粗糙地面还有待后续研究。

[1]YEE K S.Numerical solution of initial boundary valueproblems involving Maxwell's equation in isotropic media[J].IEEE Transactions Antennas Propagate,1966,14(4)：302-307.

[2]葛德彪,闫玉波.电磁波时域有限差分方法[M].西安：西安电子科技大学出版社,2005.

[3]KUNZ K S,LUEBBERS R J.The finite difference time domain method for electromagnetic[M].Boca Raton,FL：CRC Press,1993.

[4]MUR G.Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic filed equations[J].IEEE Transactions Electromagn.Compat,1981,23(4)：377-382.

[5]HASTING F D,SCHNEIDER JB,BROSCHAT S L.A Monte-Carlo technique for rough surface scattering[J].IEEE Transactions Antennas Propagate,1995,43(1)：1183-1191.

[6]GARCIA SG,LEE T W,HAGNESS SC.On the accuracy of the ADI-FDTD method[J].IEEE Antennas Wireless Propagation Letter,2002,1(1)：31-34.

[7]WANG S,CHEN J.Pre-iterative ADI-FDTD method for conductive medium[J].IEEETransactions Microwave Theory Technology,2005,53(6)：1913-1918.

[8]黄志祥,沙 威,吴先良,等.辛FDTD算法[J].系统工程与电子技术,2009,31(2)：456-458.

[9]王建永,李庆武.一种新的FDTD算法[J].苏州科技学院学报,2009,26(1)：72-75.

[10]LI E S,SARABANDI K.Low grazing incidence millimeter-wave scattering models and measurements for various road surface[J].IEEE Transactions Antennas Propagate,1999,47(5)：851-860.

[11]李灵侠,张 民.路面系统电磁散射特性的研究[J].内江科技,2009,30(4)：74-75.

[12]马宝科,郭立新,崔佳庆,等.地面电磁(光)波散射特性研究[J].西北工业大学学报,2007,27(6)：527-530.

[13]张晓燕,盛新庆.地下目标散射的FDTD计算[J].电子与信息学报,2007,29(8)：1997-2000.

[14]TSANG L,KONG J A,DING K H.Scattering of electromagnetic waves[M].New York：John Wiley&Sons Inc,2001.

[15]WANG J R,SCHMUGGE T J.An empirical model for the complex dielectric permittivity of soils as a function of water Content[J].IEEE Transactions on Geoscience and Remote Sensing,1980,18(4)：288-295.