椭圆轨道拱线相位调节方法研究

符 俊,周 英,张士峰,蔡 洪

(国防科学技术大学 航天与材料工程学院,湖南 长沙 410073)

0 引言

一般来说,共面椭圆轨道转移主要可分为三种情况：两个椭圆轨道的拱线相同,仅大小不同;两个椭圆轨道大小相同,但拱线不同;两个椭圆的大小和拱线均不相同[1]。第二种转移中,仅改变拱线的相位(即改变ω)而不改变其他轨道根数。其中：由于两椭圆轨道相交,可在交点处施加一次速度冲量改变拱线的相位,但该方法消耗的能量较大[1]。采用能量最省的最优轨道转移中,研究自由时间最省能量的最优轨道转移方法常需解决施加速度冲量的次数、位置和方向[2]。在多数最优轨道转移中,除施加速度冲量的方向要求与当地速度方向一致(如经典的霍曼转移)外,另两个问题均很难解决。本文根据文献[3]提出的对称转移轨道,基于对称转移轨道用遗传算法对最省能量椭圆拱线相位调节方法进行了研究。

1 单脉冲转移

单脉冲转移如图1所示。图中：下标I、F分别表示初始和目标轨道。对相交轨道的单脉冲转移,其速度冲量的施加点必须是两个椭圆的交点[2],即点C或点D。

图1 共面椭圆轨道单脉冲转移Fig.1 Single pulsetransfer of coplanar elliptical orbit

设变轨点为C,其在初始与目标轨道中的位置可用真近点角表示,分别为

式中：Δω为需调整的相位角。在点C,令初始轨道中航天器的速度及其倾角分别为vI,ΘI,目标轨道中航天器的速度及其倾角分别为vF,ΘF。因两椭圆大小相同,仅拱线方向不一致,故有

则变轨所需的速度冲量大小

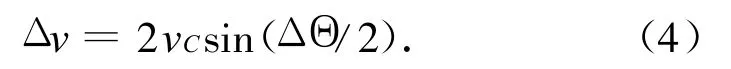
式中：ΔΘ=ΘF-ΘI。又因

故速度冲量可表示为

式中：μ为地球引力常数;e为偏心率;p为半通径。施加速度冲量的方向为径向。可证明,若在交点D进行变轨,所需的Δv与上述结果相同。

2 对称转移

对称转移如图2所示。图中：下标T表示转移轨道。转移轨道与初始与目标轨道均相切。与霍曼转移类似,在对称转移中,先沿航天器速度方向施加一次速度冲量,使航天器进入转移轨道,再在转移轨道和目标轨道的切点处施加第二次速度冲量,使航天器进入目标轨道。由于初始轨道与目标轨道关于转移轨道的主轴对称,这种转移方法称作对称转移。因它已确定了施加速度冲量的方向和次数,故对称转移的关键是求解最优变轨点的位置,使轨道转移需要的特征速度最小。

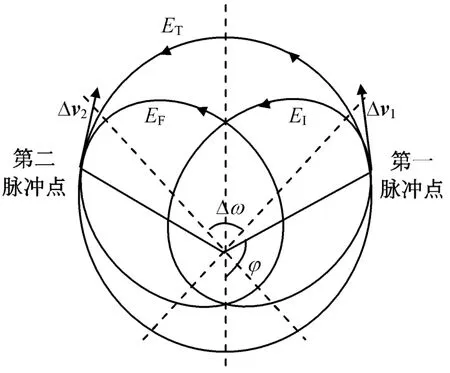
图2 对称转移Fig.2 Symmetric transfer

首先以转移轨道的主轴为极轴,实焦点为极点建立极坐标系。设φ为变轨点在转移轨道中的真近点角,则最优变轨点的位置可用极坐标表示。建立初始轨道的曲线方程,在极坐标系中可表示为

转移轨道的曲线方程为

式中：p1,p2为半通径;e1,e2为偏心率。在最优变轨点处,应满足关系

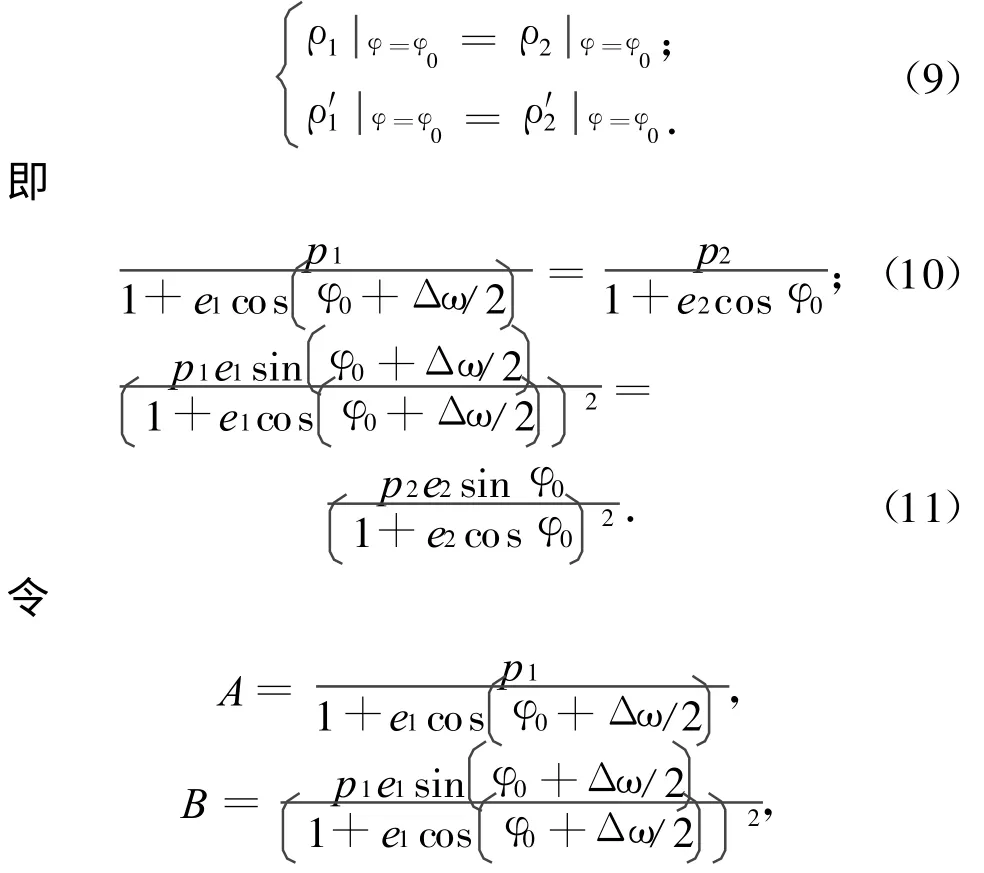
则转移轨道的偏心率和长半轴分别为

解出转移椭圆后,可得转移轨道中最优变轨点处的速度

初始椭圆轨道中最优变轨点处的速度

由此可得第一次变轨需要的速度冲量

由于第二次变轨点的位置与第一次变轨点的位置关于转移轨道的主轴对称,它需要的速度冲量大小与第一次变轨相同,故整个变轨过程需要的总速度冲量大小为2Δv。

3 遗传算法

遗传算法是模仿自然界生物进化机制的随机全局搜索和优化方法,是一种高效、并行、全局搜索的方法。它能在搜索过程中自动获取和积累有关搜索空间的知识,并以自适应的控制搜索过程求得最优解。遗传算法运算流程如图3所示[4]。

图3 遗传算法运算流程Fig.3 Operation flowchart of genetic algorithm

4 仿真

以椭圆轨道为例,分析拱线相位调节中的能量需求。用遗传算法计算最优变轨点的位置。本文取遗传算法的参数为：最大遗传代数50,代沟0.9,选择使用随机遍历抽样,交叉概率0.7,变异概率0.017。

4.1 最优变轨点的位置与a,e,Δω的关系

最优变轨点的位置决定了对称转移最小特征速度的大小。在对称转移中,影响最优变轨点位置的因素有初始轨道的半长轴a、偏心率e和拱线的Δω。

a)半长轴

a决定椭圆轨道的大小。e=0.5,Δω=4°时,仿真所得不同a的最优变轨点位置如图4所示。因e为定值,且地球轨道的近地点地心距应大于地球半径,故取a的范围为13 000～30 000 km。由图4可知：最优变轨点的位置不随a而变,即初始椭圆轨道的大小不影响最优变轨点在转移椭圆中的位置。

图4 不同a的最优变轨点位置Fig.4 Position of optimum transfer point with various semimajor axis

b)偏心率

e决定椭圆轨道的形状。a=30 000 km,Δω=4°时,仿真所得不同e的最优变轨点位置如图5所示。e范围为0.1～0.9。由图5可知：最优变轨点在转移椭圆轨道中的真近点角随e增加而单调增大,即初始椭圆轨道越扁,最优变轨点的真近点角就越大。

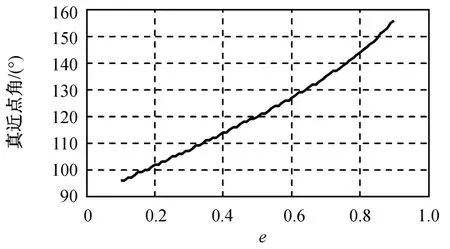
图5 不同e的最优变轨点位置Fig.5 Position of optimum transfer point with various eccentricity

c)拱线相位调节角度

初始椭圆轨道a=18 000 km,e=0.6时,仿真所得不同Δω的最优变轨点位置如图6所示。

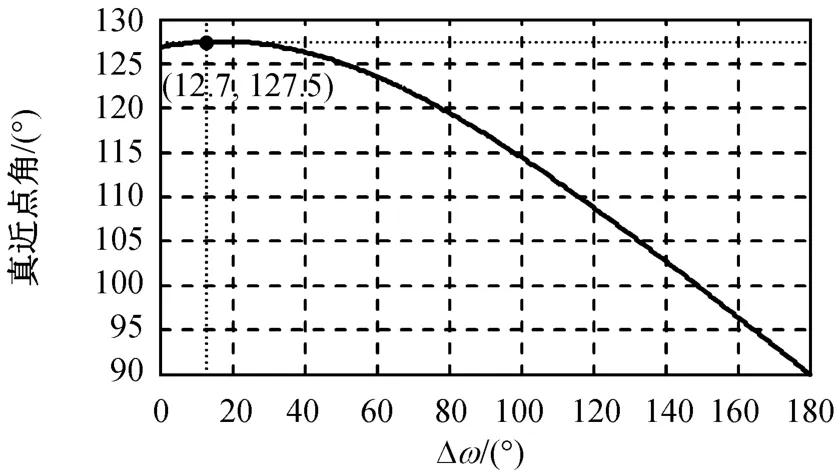
图6 不同Δω的最优变轨点位置Fig.6 Position of optimum transfer point with various angle of apsidal line

由图6可知：最优变轨点的位置不仅与椭圆的形状有关,还受Δω的影响。当Δω＜12.7°时,最优变轨点在转移轨道中的真近点角随Δω增大而增大;当Δω＞12.7°时,最优变轨点在转移轨道中的真近点角随Δω增大而减小,且当Δω=180°时,f=90°,转移轨道成为圆轨道,对应的轨道转移如图7所示。

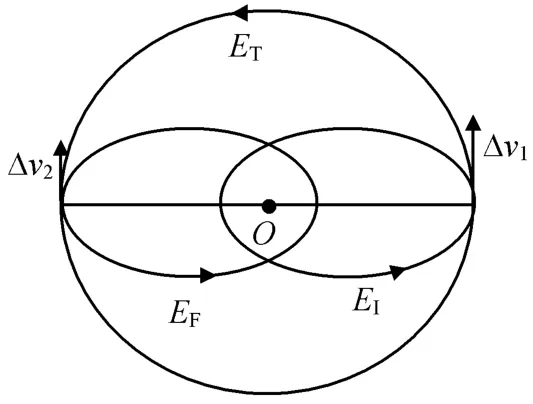
图7 Δω=180°时椭圆轨道的对称转移Fig.7 Symmetric transfer of elliptical orbit withΔω=180°

4.2 单脉冲转移和双脉冲对称转移比较

设椭圆轨道参数为：a=20 000 km,e=0.6,计算Δω在0°～10°时的能量需求,结果分别如图8、9所示。

不同转移相位时单脉冲转移和双脉冲对称转移需要的速度冲量计算结果见表1。由表1可知：用对称转移进行拱线相位调节所需要的速度冲量约为单脉冲转移的50%,方法明显更优。

图8 优化过程中目标函数和种群均值Fig.8 Target value and mean value of population in optimization

图9 拱线相位调节需要的速度冲量Fig.9 Velocity impulsewith various apsidal line angle

表1 单脉冲转移和对称转移需要的速度冲量Tab.1 Velocity impulse of single-impulsetransfer and symmetric transfer

5 结束语

基于LAWDEN,PRIMMER的研究,本文对大小相同的椭圆拱线相位调节方法进行了研究,提出了单脉冲转移和双脉冲对称转移方法。讨论了对称转移,用遗传算法求解最优变轨点位置,获得了最优变轨所需特征速度的求解方法。仿真结果表明：对称转移较单脉冲转移更省能量。

[1]郗晓宁,王 威.近地航天器轨道基础[M].长沙：国防科学技术大学出版社,2003.

[2]GOBETZ F W,WASHINGTON M,EDELBAUM T N.Minimum-impulse time-free transfer between elliptic orbits[R].NASA Contractor NASI-4688,1966.

[3]LAWDEN D F.Impulsive transfer between elliptical orbits：optimization techniques[A].LEITMANN G.New York：Academic Press,1962.

[4]雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2005.