运载器末助推段非线性姿态控制器设计

孙 平,刘 昆

(国防科学技术大学 航天与材料工程学院,湖南 长沙 410073)

0 引言

某小型固体运载器采用四级结构设计方案,前三级由固体发动机提供推力,第四级为液体推进上面级模块,它完成飞行中各级的姿态控制任务及末助推变轨推进,使飞行器进入椭圆过渡轨道,同时进行组合制导,对主动段制导误差、关机延时量随机偏差及发动机后效偏差进行精确修正[1]。在末助推飞行阶段,因前面各级姿控的消耗,推进剂贮箱不再被液体填满,此时飞行器的运动将引起剩余推进剂的运动(晃动)[2]。推进剂晃动与飞行器姿态运动通过惯性力的相互作用直接耦合,该耦合作用对飞行器姿态运动的稳定性和控制系统设计产生直接影响[3]。

为了解和掌握推进剂晃动规律,国内外对液体晃动作了大量试验和理论研究,通过假设液体为不可压缩和无旋,建立了描述液体晃动的等效力学模型。其中广泛应用的有单摆和等效弹簧-质量两种模型[4]。姿态控制系统设计中,对晃动不稳定问题常采用被动控制与主动控制两种策略,前者即在贮箱内设置防晃障板,提高晃动阻尼或改变贮箱结构,提高晃动频率;后者则通过改进控制器设计实现对晃动不稳定的抑制,如文献[5]通过限制控制器在晃动频段的幅频特性,增大控制器在晃动频段的相位超前实现晃动抑制;文献[6]设计了自适应控制器完成卫星机动变轨过程中的控制;文献[7]采用输入成型技术抑制大挠性航天器的晃动等。

近年来,基于状态相关黎卡提方程(SDRE)的控制器设计在飞行器控制中获得了广泛应用[8-10]。它提供了一种系统、有效的非线性控制器设计技术。在采用单摆模型近似晃动质量推导晃动运动与姿态运动的动力学方程的基础上,本文采用SDRE方法,综合动态逆控制设计了有晃动运动时的飞行器姿态控制律,通过状态反馈实现姿态跟踪和晃动抑制,并进一步考虑控制器的工程应用[11]。

1 运动学与动力学模型

考虑俯仰平面内的运动,采用单摆模型等效晃动。在末助推无动力飞行阶段,有一个液体推进剂贮箱的运载器受力如图1所示。图中：Ob-XbYbZb为箭体坐标系,其中原点Ob为运载器刚体部分及未晃动推进剂部分所确定的质心。定义运载器的俯仰角为θ,液体晃动等效摆长为l、悬挂点距离运载器质心为b的单摆模型。单摆偏离ObXb轴的角度为φ。

图1 运载器受力示意Fig.1 Force of launcher

将运载器质心加速度矢量投影至Ob-XbYbZb系的OXb、OZb轴,有

式中：vx,vz分别为运载器速度矢量在Ob-XbYbZb系ObXb、Ob Zb轴的投影。

定义固联于单摆的体坐标系xoz：原点o固联于摆锤;ox轴沿摆杠方向;oz轴垂直于ox轴指向左侧。将摆锤质心加速度矢量投影到xoz系的ox、oz轴,有

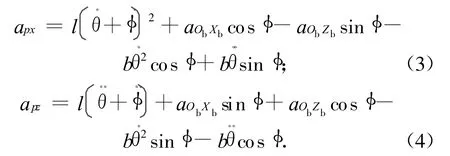
式中：apx,apz分别为单摆质心沿和垂直摆杆方向的运动加速度。

将单摆和运载器视作相互施加力的作用的独立部分。用牛顿力学分析其受力状况。定义单摆产生的阻尼力矩

式中：Cφ为阻尼力矩系数。

对摆锤质心,将牛顿第二定律方程投影到xoz系的ox、oz轴,有

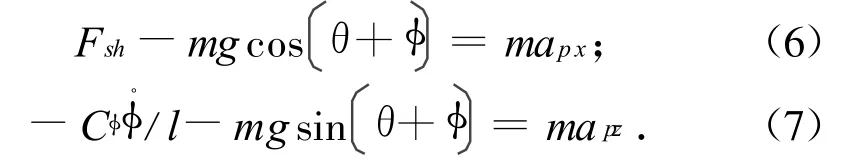
式中：m为摆锤质量;g为重力加速度;Fsh为作用于单摆质心的沿摆杆方向的外力,将摆锤作为质点。

对运载器质心,将牛顿第二定律方程投影到Ob-XbYbZb系的ObXb、ObZb轴,有

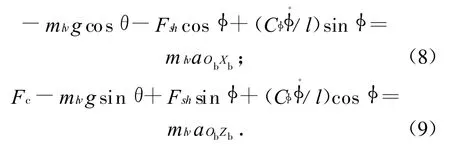
式中：Fc为作用于运载器质心的沿ObZb轴方向的外力;mlv为运载器刚体部分及未晃动推进剂部分的质量。

绕运载器ObZb轴的转动动力学方程为

式中：Lc为Fc至点Ob的力臂;为箭体绕ObYb轴的转动惯量。

式(1)～(10)即为有晃动质量的运载器动力学方程。

2 姿态控制器设计

姿态控制器设计可分为三步：一,综合状态相关黎卡提方程方法与动态逆方法设计状态反馈非线性姿态控制器,控制系统中的状态变量跟踪制导指令;二,因单摆运动是为实现晃动模拟而人为引入系统,不可实际测量,为控制律能实现,采用快速输出采样技术实现对状态的估计;三,需对连续的控制指令进行调制,获得脉冲信号控制发动机开关状态[12-14]。

2.1 SDRE与动态逆相结合的控制律设计

SDRE方法用于处理输入仿射非线性系统的状态反馈控制器设计。将系统

改写为

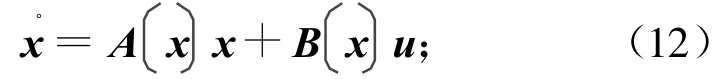
状态反馈控制器为

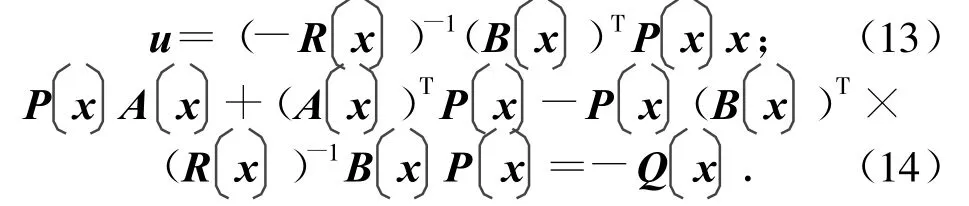
式中：x为系统状态变量;u为系统输入变量;f(x)为系统状态矩阵的非线性表达式,且f(x)=A(x)x;B(x)为系统的输入阵;P(x)为状态相关黎卡提方程的解;Q(x),R(x)为设计参数,分别为半正定和正定阵。

动态逆方法是通过设计控制器与非线性系统中某些运动对消,使系统达到期望的运动。对非线性系统

可设计控制器为

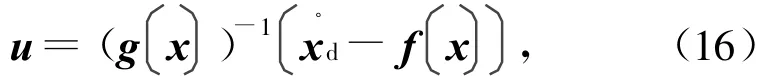
用SDRE与动态逆综合方法进行控制律设计要求[A(x) B]对x为点点可控。在此前提下,SDRE方法得到的控制律为式(13),动态逆方法所得的控制律为

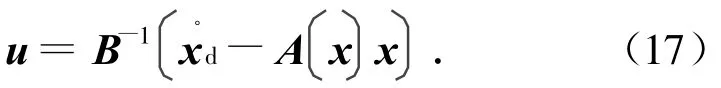
选择

代入式(17),得

式中：Ad为期望的A。比较式(19)、(13),可得

至此,通过SDRE方法实现了动态逆控制的实质,选择Q(x)并计算式(13)、(14)即可得状态反馈控制律u。

用上述方法计算u时,关键是将系统动态方程写成式(12)中的形式。

根据控制器设计需求,将式(1)～(10)描述的系统改写成的形式,选择状态变量为

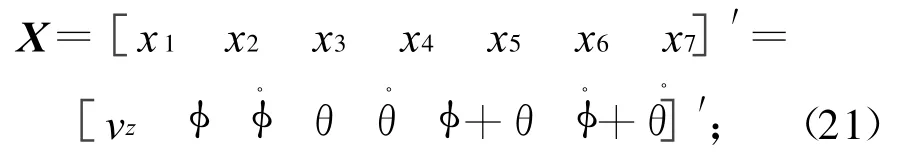
控制变量

则矩阵A(x)、B(x)中非零系数的表达式为

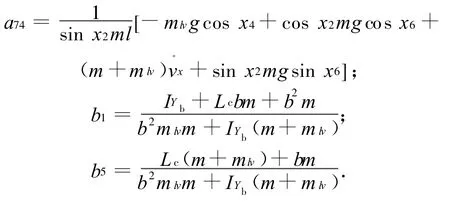
2.2 反馈控制律实现

前文设计的控制方法是基于状态反馈控制,但实际中,由于单摆模型仅是对晃动的机械近似,与其相关的变量的状态不可量测。为此,引入快速输出采样技术,通过对输出信号采用多速率观测器重构系统状态,实现离散状态反馈。实现方法如下[10]。

设τ为采样周期的离散时间系统为

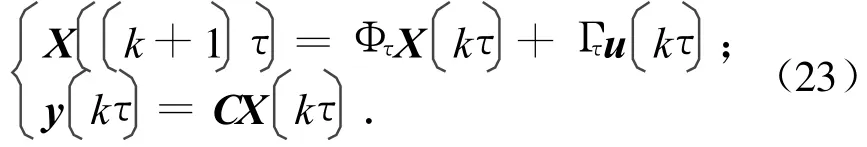
式中：Φτ,Γτ,C分别为以采样周期获得的离散系统的状态阵、控制阵和输出阵。满足(Φτ,Γτ)能控,(Φτ,C)能观测,另输入信号在间隔τ内保持不变,对输出信号以Δ=τ/N,N≥v为间隔进行采样。此处：v为系统式(23)的能观测性指数,得采样间隔为Δ的系统

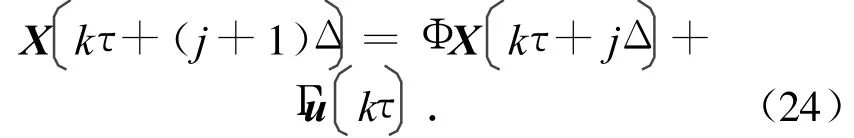
式中：j=0,1,…,N-1。令

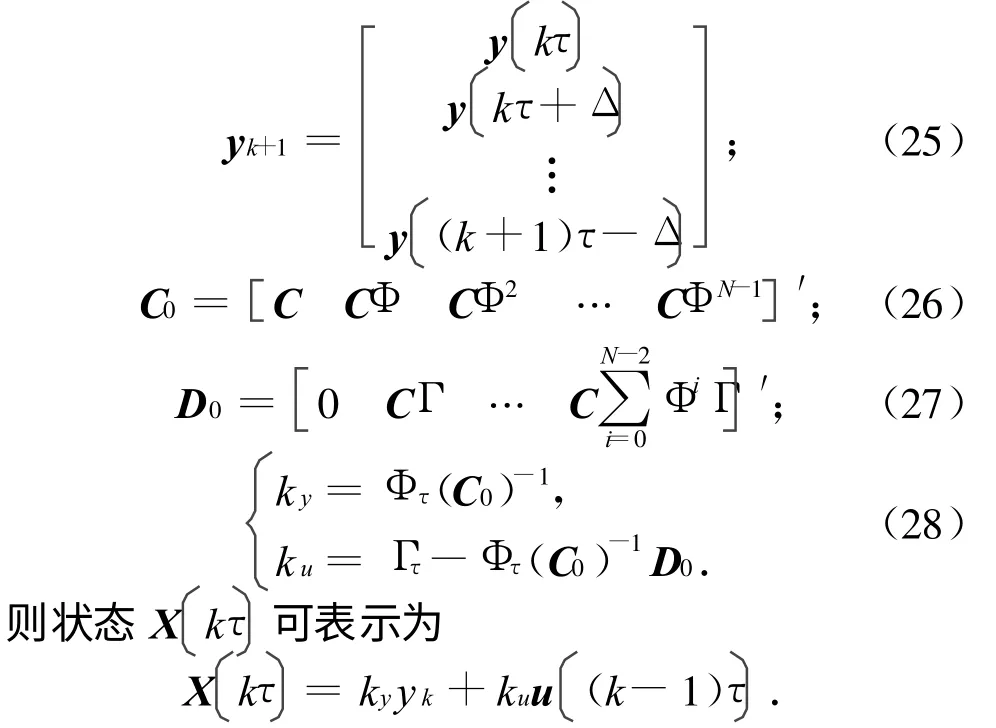
这样,就实现了通过对输出信号采用多速率观测器重构系统状态,进而可实现所设计的状态反馈控制律u。系统中实现姿态控制的执行机构是固定推力的液体发动机,需对控制器产生的连续控制信号进行调制,通过改变两次喷气间的间隔时间,实现对飞行器姿态的控制。

3 仿真

设飞行器模型的参数为：mlv=500 kg,m=50 kg,l=0.35 m,b=1.1 m,Fc=25 N,Lc=0.4 m,Cφ=0.2,g=9.18 m/s2;控制器的计算周期50 ms,输出采样周期5 ms,初始状态选择φ=2°,=4(°)/s,θ=10°,=5(°)/s,分别在姿态角跟踪常值姿态角指令θcmd=5°和正弦姿态角指令θcmd=条件下进行仿真,所得结果如图2～5所示。由图可知：在本文设计的控制器作用下,对常值姿态角和正弦姿态角指令的跟踪均可在10 s内收敛,液体晃动也能得到稳定。跟踪常值姿态角时,液体晃动等效摆的运动可稳定在0附近,而跟踪正弦姿态角时,等效摆的晃动将稳定在一较小的振动幅度内。推进剂的晃动能获得稳定。

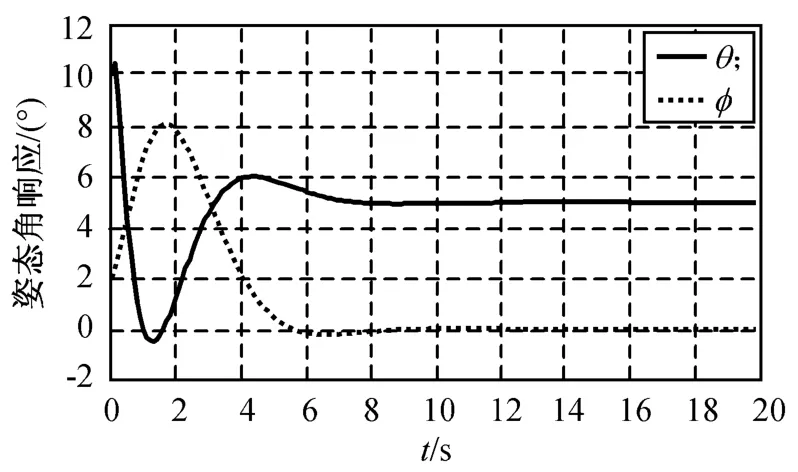
图2 常值输入时的姿态角响应Fig.2 Attituderesponse under constant input

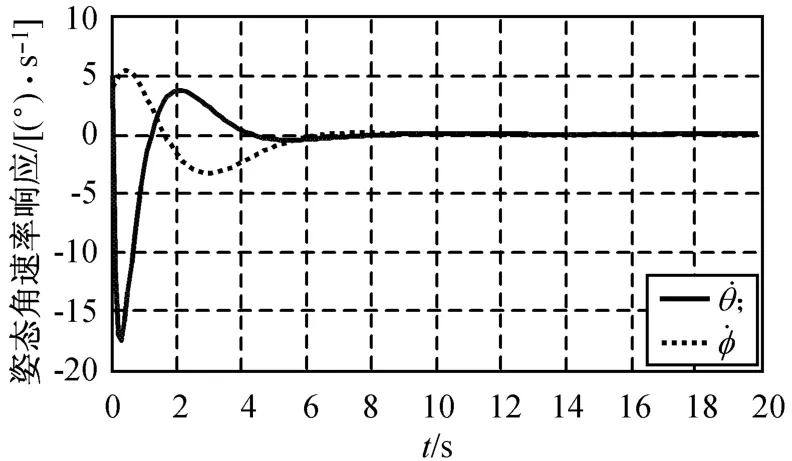
图3 常值输入时的角速率响应Fig.3 Angle rateresponse under constant input

图4 正弦输入时的姿态角响应Fig.4 Attituderesponse under sine input

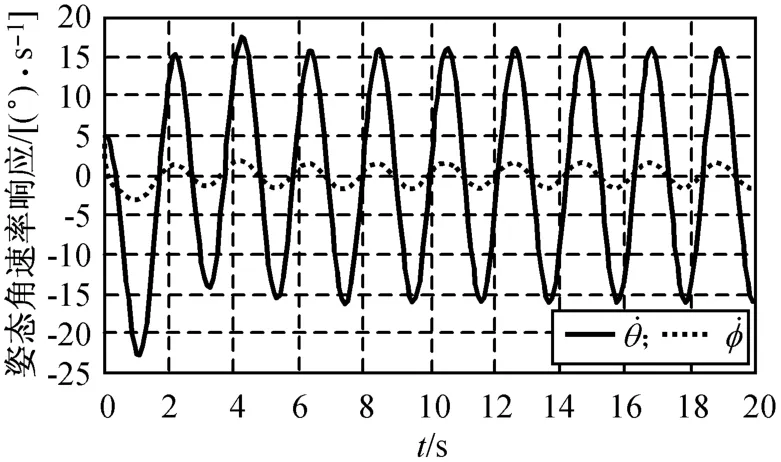
图5 正弦输入时的角速率响应Fig.5 Angle rate responseunder sine input

4 结束语

针对运载器末助推段推进剂晃动与姿态动力学间的耦合,本文采用单摆模型近似晃动质量,推导了晃动运动与姿态运动的动力学方程,并在此基础上给出了系统的状态相关因子表达形式,设计了基于SDRE方法和动态逆方法的状态反馈控制律对运载器姿态运动进行稳定,同时抑制晃动作用。由于实际中晃动运动的状态不可测量,引入快速输出采样技术估计系统状态,使所设计的控制律可在工程中实现。数值仿真结果验证了控制器的有效性。

[1]AMATO F,AMBROSINO G,FILIPPONE E,et al.Attitude control of a small conventional launcher[C]//Proceedings of the 2002 IEEE International Conference on Control Applications.Glasgow,UK：IEEE,2002：284-289.

[2]NICHKAWDE C,HARISH P M,ANANTHKRISHNAN N.Stability analysis of a multibody system model for coupled slosh-vehicle dynamics[J].Journal of Sound and Vibration,2004(275)：1069-1083.

[3]SHEKHAWAT A,NICHKAWDE C,ANANTHKRISHNAN N.Modeling and stability analysis of coupled slosh-vehicle dynamics in planar atmospheric flight[C]//The 44th AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada：AIAA,2006：006-427,1-20.

[4]陈存芸.运载火箭三级无动力飞行段晃动稳定性研究[J].上海航天,2004,21(4)：29-33.

[5]KIM D H,CHOI J W.Attitude controller design for a launch vehicle with fuel-slosh[C]//AIAA Guidance,Navigation,and Control Conferenceand Exhibit.Denver,CO：AIAA,2000：3851,235-240.

[6]SHAGEER H,TAO G.Modeling and adaptive control of spacecraft with fuel slosh：overview and case studies[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Hilton Head,South Carolina：AIAA,2007：6434,1-19.

[7]ABOEL-HASSAN A,ARAFA M,NASSEF A.Design and optimization of input shapers for liquid slosh suppression[J].Journal of Sound and Vibration,2009(320)：1-15.

[8]PARRISH D K,RIDGELY D B.Attitude control of a satellite using the SDRE method[C]//Proceedings of the American Control Conference.Albuquerque,New Mexico：[e.n.],1997：942-946.

[9]MENON P K,SWERIDUK G D,VADDI SS,etal.Nonlinear discrete-time design methods for missile flight control systems[C]//AIAA Guidance,Navigation,and Control Conference.Providence,RI：AIAA,2004：2514,1-16.

[10]BRACCI A,INNOCENTI M,POLLINI L.A Newton algorithm for implementation of SDREcontrollers[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.San Francisco,CA：AIAA,2005：6386,1-12.

[11]SAAJ M C,BANDYOPADHYAY B,UNBEHAUEN H.A new algorithm for discrete-time sliding-mode control using fast output sampling feedback[J].IEEE Transactions on Industrial Electronics,2002,49(3)：518-523.

[12]SHANKAR P,YEDAVA LLI R K,DOM AN D B.Dynamic inversion via state dependent Riccati equation approach：application to flight vehicles[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Austin,TX：AIAA,2003：5361,1-9.

[13]SHANKAR P,YEDAVALLI R K,DOMAN D B.Stability domain estimation for dynamic inversion embedded SDRE flight controller[C]//AIAA Guidance,Navigation,and Control Conferenceand Exhibit.Providence,Rhode Island：AIAA,2004：4871,1-11.

[14]ERDEM E B,ALLEYNE A G.Design of a class of nonlinear controllers via state dependent Riccati equations[J].IEEE Transactions on Control Systems Technology,2004,12(1)：133-137.