利用热平衡试验稳态数据修正对接机构热模型

李 鹏 ,张崇峰,陈宝东,柏合民,秦 彦,来霄毅

(1.上海宇航系统工程研究所,上海 201108;2.上海航天技术研究院,上海 201109)

0 引言

对接机构是实现空间对接的关键设备[1-2]。为保证对接机构工作可靠,必须在地面进行充分的空间环境真空热试验(包括热平衡试验和热真空试验)[3]。热平衡试验完成后的一项重要工作是利用热平衡试验的温度数据对热分析用的热模型进行修正,随后利用修正的热模型预示对接机构在轨温度。对热模型修正方法已进行了大量研究,但在实际工程应用中还存在诸多问题,实用化不足,在建立对接机构热模型进行热分析的每个步骤的处理中都会不同程度产生计算结果与试验值的偏差[4-6]。基于对计算值和试验值差异原因的分析,本文利用热平衡试验稳态工况的试验数据对对接机构热模型进行修正,研究了热网络方程修正的实用化方法。

1 热平衡试验数据与计算结果比较

对接机构是目前航天器上结构最复杂的外部机构之一,其中有大量的活动部件。为保证其能在恶劣的空间环境中正常工作,根据被动热控措施为主、主动热控措施为辅的原则,选用热控涂层、多层隔热组件、主动电加热的热控措施对对接机构进行了热控设计。对接机构热控件如图1所示。为验证热控设计的有效性进行了对接机构热平衡试验。共进行了4个工况的稳态试验。由试验结果与仿真数据比较可知：绝大多数部件温度试验值均低于仿真值,且不同位置部件的温度试验值与仿真值的差异并不完全相同,其中对接框及与之接触较好部件的温度试验值较仿真值低约10～15℃,但两者温度变化的趋势基本一致,而对接环及与对接环接触较好部件的温度试验值与仿真值虽分布趋势基本一致,但两者相差较大,最大达25℃。

2 结果偏差分析

本文对接机构热分析采用节点热网络方法[7]。建模计算主要包括热分析物理模型建立、网格划分、热网络数学模型建立和方程组求解共4个步骤。其中求解方程组时,选用了先进的求解方法,产生的误差很小,因此导致对接机构热分析数值计算结果与试验值偏差的原因主要是：由于对接机构各单机设备结构复杂、外形极不规则,为便于计算,其外形和结构需分别进行相应的规则化与简化处理,上述处理后的热分析物理模型与原对接机构实体存在一定的差异;通过网格划分进行单元处理时,单元的大小和类型设置不合理会使计算结果偏离试验值;热网络方程建立过程中,选取的物理参数不准确造成热网络方程所描述的换热关系与实际存在偏差,此处物理参数包括材料的导热系数、表面辐射特性、接触热导等。

对接框及与之接触较好部件大部分包覆在多层隔热材料内,计算结果偏高的主要原因是：单元划分不合理;多层隔热组件实际实施的包覆效果与热分析模型中的理想效果存在差距,不可避免地存在漏热。对接环及与对接环接触较好部件均暴露在冷环境中,计算结果偏高的主要原因是对接环表面实际发射率值高于计算模型中的设定值。

3 热模型修正

为顺利进行热分析,建立物理模型时,必须作合理的规则化与简化处理,该处理导致计算结果必然存在偏差。如能尽可能按质量和有效表面积与实际部件相同的原则建模,该偏差不会很大,同时可通过对热网络方程的修正,使物理模型建立时由外形和结构处理产生的偏差进一步减小到允许的范围。因此,本文仅针对偏差分析中的后两个原因,修正对接机构的热模型,而重点是热网络方程的修正。

3.1 单元划分修正

对接锁系是对接机构上最重要的活动部件之一,主要由12把对接锁和2个对接锁驱动组成,每把对接锁的锁壳内有2个结构较复杂的锁钩,锁壳外部是传递装置,保证对接锁系中锁钩同步工作。热分析建模时,将锁壳和内部的锁钩视作一个整体,进行体单元的网格划分。热平衡试验时,测温点布置在锁壳上,发现试验值低于仿真值。分析发现将锁壳和锁钩作为一个整体进行单元划分并不合理,因为锁壳与锁钩是接触连接,作为一个整体会增大两者的导热影响,增加两者温度的拉平趋势,使锁壳上的温度计算值偏高于试验值。本文修正单元划分时,对锁壳和锁钩独立建立物理模型,再对锁壳进行面单元网格划分,锁钩进行体单元网格划分,最后两者间建立接触热耦合。根据此分析方法,捕获锁单机也进行了相应的单元划分修正。

3.2 热网络方程修正

3.2.1 传统热网络方程修正方法

利用热试验数据修正热模型关键修正热网络方程,目前的修正方法多为基于热网络方程的系数修正[8]。航天器的稳态热网络方程可简单描述为

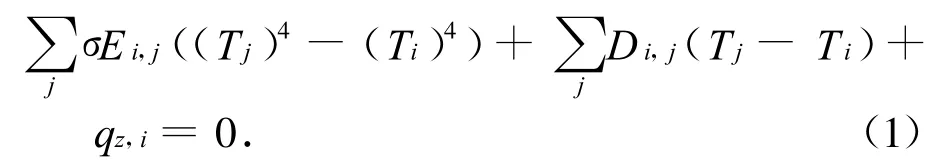
式中：σ为斯忒藩-波尔兹曼常量,且σ=5.67×10-8W/(m2◦K4);Ti,Tj分别为节点i、j的温度;Ei,j,Di,j分别为节点i、j间的热辐射和热传导网络系数;qz,i为总热流,包括内热源和空间外热流[4]。显然,式(1)中计算系数的正确与否直接影响温度仿真计算结果的真实性。

热网络方程修正,就是将试验所得温度数据代入式(1),通过一定的数值方法获得热网络系数Ei,j,Di,j,qz,i的修正值,直接对热网络系数进行修正。该方法的目标和物理意义明确,理论研究较深入,但面临问题不少,主要是：待修正的未知数过多,试验工况不足,修正模型为不定方程组;试验测点与模型节点不统一,部分模型节点无温度测点等,导致数据处理和工程实现困难[7-8]。

区域内降雨量大，且集中，雨水的下渗在裂缝中产生动水压力，不但降低土体的抗剪强度，还提高重量，为滑坡的最后形成起到推波助澜的作用。经调查，滑坡的产生与强降雨在时间上一致，说明雨水的作用对滑坡变形产生较大的影响，是本滑坡变形的重要影响因素。

3.2.2 参数化节点群整合方法

对接机构结构非常复杂,热分析时节点划分较多,这样需修正的系数也就非常多,难度较大。根据文献[8]的参数化和节点群概念,本文进一步改进和提出了参数化节点群整合方法,该法可减少需修正的系数数量。热网络方程修正时,将该方法与分级修正技术和局部修正组合,可提高热网络修正方法的实用性[4]。

a)热网络方程整合

将航天器中有相同物性参数(导热系数、表面辐射特性等)的计算节点组成节点群。设航天器有节点U个,组成的节点群V个,即节点群s=[s1s2s3… sV],节点群si中有节点Mi个,sj中有节点Mj个。基于文献[5]的节点对节点群整合方程,本文采用节点群间的热网络整合方程,建立节点群间的稳态热网络关系为

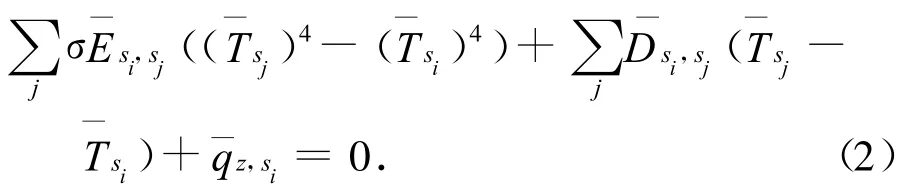
式中：

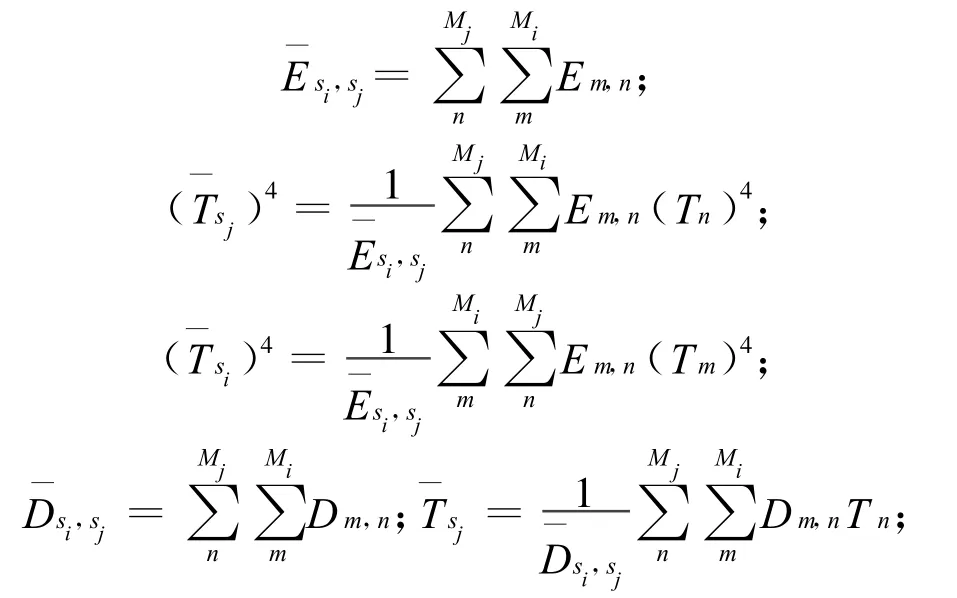
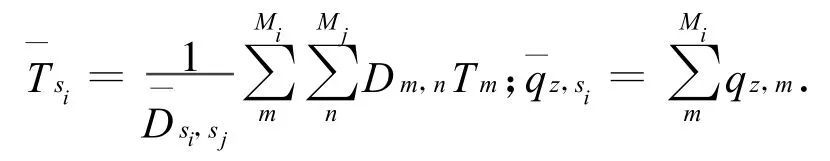
整合热网络方程组前,需修正的是多个节点间的热网络系数,如Ei,j表示两两节点间的热辐射网络系数,则整个航天器热网络方程组中共有热辐射网络系数U2个,考虑热辐射网络系数的互换性,则需修正的热辐射网络系数为U2/2个[2]。热网络方程组整合后,需修正的是节点群间的热网络系数,如对共有V2/2个。对复杂航天器,通常U≫V,故整合后需修正的系数大量减小。

参数化处理的基本要点是从Ei,j,Di,j中分离出接触传导系数h、等效导热系数keff、太阳吸收率αs和表面发射率ε等各种物性参数,在进行模型修正工作时不直接修正Ei,j,Di,j,而直接修正这些关键的物性参数,同时根据物理意义对待修正的参数进行限定,即将其变化范围控制在合理区域内。多种情况下部分节点的上述物性参数极可能相同,则通过热网络方程整合后,就可进一步减少修正系数的数量。

将式(2)参数化处理后,得参数化热网络整合方程为

进一步参数化后,需要修正量则是物性参数(如h,keff,αs,ε等),则需修正量进一步减少。如,某节点群i对其他节点群形成的修正量为V个,参数化后修正量变为1个物性参数εi,因此上述V2/2个修正量,参数化后变成了V个εi。

3.2.3 非直测节点温度认定的外推方法

由上述分析可知：修正模型需要获知每个节点群中所有节点的试验温度,但实际试验不可能在每个节点处布置测温点。因试验值与计算值相差较大,如用计算值替代无测点的节点温度试验值可能产生较大误差,但可用计算获得的温度分布状况和测得的温度,由外推得到其他节点的试验温度。

物体温度稳定后,物体内部的导热热流一定。设节点的计算温度为Tc,i,相应节点试验温度为Tx,i,i=1,2,…,M,其中试验真实测得温度对应节点A,节点B、A相邻,则计算模拟时节点A、B的导热热流

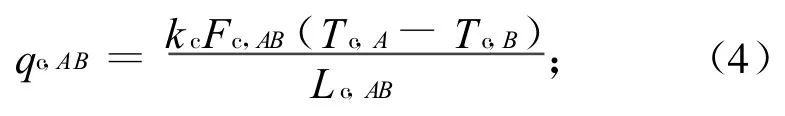
试验时节点A、B的导热热流

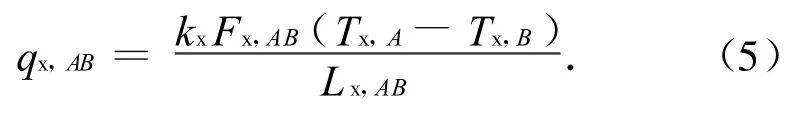
式中：kc,kx分别为计算和试验时的等效导热系数;Lc,AB,Fc,AB,Lx,AB,Fx,AB分别为计算时和试验时节点间有效导热距离与有效导热面积,且Lc,AB=Lx,AB,Fc,AB=Fx,AB。

式(4)、(5)相除,整理后得

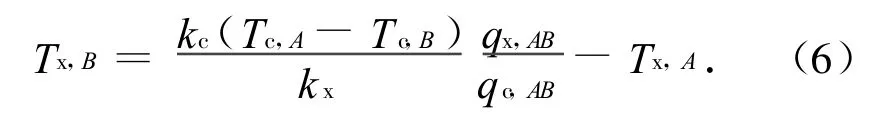
其中,qc,AB,qx,AB可由计算与试验时的边界条件确定。由式(6)可得与节点A相邻的所有节点的试验温度。用相同方法可进一步外推确定其他相邻近节点的试验温度,依此可得节点群内所有节点的试验温度。

3.2.4 热网络方程修正算例

因热平衡的试验工况有限,无足够试验数据进行整星的热网络修正,本文采用局部热网络参数修正法,即首先分析试验值与仿真值的差异,确定引起差异的决定性参数,然后建立关于决定性参数对应节点群的局部热网络方程,最后用该局部热网络方程修正决定性参数。以导向板表面发射率的修正为例进行讨论。

导向板的正面(面向外部空间)和背面(面向机构内部)进行了不同的表面处理,其中正面的处理工艺稳定性较差,须对正面的发射率作必要修正。根据考虑主要因素、忽略次要因素的原则,建立导向板正面节点群的局部热网络整合方程。热试验时,导向板正面面向冷黑热沉,其与热沉环境存在主要的辐射换热,则导向板正面节点群局部整合方程中仅考虑与试验热沉环境的辐射换热,以及与对接环和捕获锁的导热。对接机构上有导向板3个,每个导向板正面划分有节点18个,与之有直接导热关系的对接环上节点有20个,捕获锁上有节点9个。参数化热网络方程整合前,需修正的辐射热网络系数为18个,参数化热网络方程整合后,需要修正的参数变为1个。由式(3)可得导向板正面节点群的整合热网络方程为

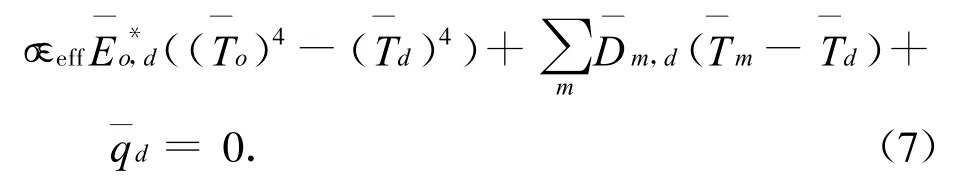
导向板局部整合热网络方程中各项系数、热流及修正计算值见表1。表中：为参数化后导向板对热沉环境的热辐射网络系数;分别为导向环和捕获锁与导向板间的热传导网络系数。由表1可知：由不同工况不同导向板的试验数据得到的修正值各异,可根据修正结果进行数据处理,如选取部分偏差较小的修正结果进行算术平均。表1中修正值相接近,其算术平均为0.34。由上述分析可知：建立局部热网络整合方程时也作了一定的简化,故通过上述局部热网络整合方程获得的修正值可能还需调整。将修正值代入对接机构热分析模型进行计算,分析结果后,最后将εeff调整为0.35作为最终修正值。可见由局部热网络整合方程得到的修正值虽然不一定就是最后的修正值,但已非常接近最后的修正值。

表1 导向板整合热网络方程中各项系数、热流及修正值Tab.1 Coefficient and fluxes in combined thermal network equations and correction values

4 修正后数据比较

用本文热网络方程的修正方法对多层隔热组件等效导热系数,对接机构和模拟边界的接触热导等物理参数进行了修正,由修正的热模型数值计算所得稳态低温和稳态高温工况的对接机构试验与计算温度分别如图2、3所示。由图可知：用修正后热模型获得的计算值与试验值非常接近,稳态低温工况下,绝大多数部件的计算与试验值温差小于5℃,极少数部件的温差小于8℃;稳态高温工况下,绝大多数部件的计算与试验值温差小于4℃,极少数部件的温差小于6℃。通过热模型的修正使温度计算值与试验值的偏差达到允许要求,表明本文的热模型修正方法可行且有效。

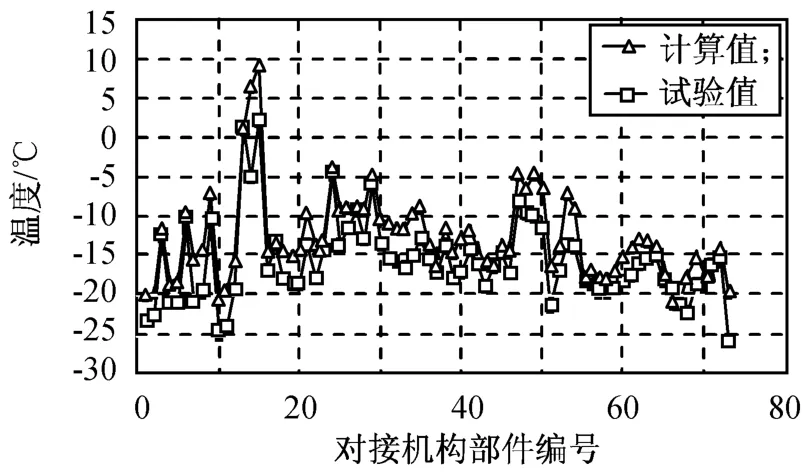
图2 低温工况下修正过的热模型的计算结果与试验值Fig.2 Calculation results using corrected model and test data in low-temperature case

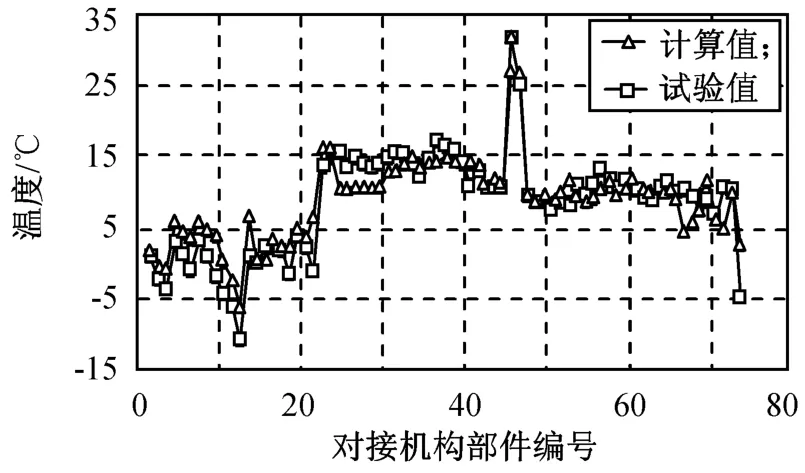
图3 高温工况下修正过的热模型的计算结果与试验值Fig.3 Calculation results using corrected model and test data in high-temperature case

5 结束语

对接机构热模型修正是完成对接机构热平衡试验后的一项重要工作。本文分析了试验值与计算值存在偏差的原因,对对接机构热模型中的单元划分和热网络方程进行了修正。热网络方程修正时采用参数化节点群整合方法,并综合分级修正和局部修正,使需要修正的系数数量大幅减少。导向板表面发射率修正算例证明了本文方法的可实施性,由修正的热模型数值计算获得温度值与试验值的比较表明对接机构热模型修正有效,为之后的对接机构在轨温度预示打下了良好的基础。

[1]DONABEDIAN M,GILMORE D G.Spacecraft thermal control handbook[M].Los Angeles,California：Aerospace Press,2002.

[2]林来兴.空间交会对接技术[M].北京：国防工业出版社,1995.

[3]黄本诚,马有礼.航天器空间环境试验技术[M].北京：国防工业出版社,2002.

[4]闵桂荣.卫星热控制技术[M].北京：宇航出版社,1990.

[5]翁建华,闵桂荣,潘增富.利用稳态数据修正航天器热网络方程及其系数[J].工程热物理学报,1998,19(2)：218-223.

[6]翁建华,潘增富.航天器热网络模型及其系数修正方法[J].中国空间科学技术,1995,15(4)：10-15.

[7]侯增祺,胡金刚.航天器热控制技术[M].北京：中国科学技术出版社,2007.

[8]李劲东.卫星热网络模型修正技术进展及其改进方法研究[J].中国空间科学技术,2004,24(3)：29-37.