高楼振动监测中的GPS与加速度计集成方法研究

戴吾蛟，伍锡锈，罗飞雪

(中南大学 信息物理工程学院测绘与国土信息工程系，长沙 410083)

高楼、电视塔以及悬索桥等许多高耸或大跨的工程结构物，在运营载荷、强风以及地震等外界因素的影响下，这些大型工程结构物都会产生振动与变形。变形过大将影响结构的正常运营，或使结构产生局部性破坏乃至倒塌。对高楼等大型结构物进行动态变形监测，可以实时监测工程结构物的健康状况，以及对其安全运营能力和寿命的评估都具有非常重要的意义［1－2]。GPS由于其高效、快速、全天候、全自动以及能够直接得到监测点的三维坐标值等优点，在大型结构物监测中得到了广泛的应用［3－4]，但是GPS的监测精度和稳定性常受到多路径效应、周跳、信号中断等异常干扰和影响［5]。此外，目前用于动态监测的GPS采样率一般为10 Hz－20 Hz，更高采样率的GPS接收机比较昂贵或者其硬件稳定性能较差，因此较低采样率问题也是实际应用中不可忽略的问题。加速度计由于其体积小质量轻，常用于测量外界荷载作用下的结构响应，并且能够得到高采样率、高精度的加速度观测值，但是加速度计不能很好的测量缓慢的近似静态振动以及其位移是通过对加速度值进行二次积分求得，初始位移和初始速度较难确定，且容易产生零点漂移误差，所以位移精度不高很难达到厘米级［2]。

由于GPS与加速度计等传统传感器在大型结构物动态变形监测中各有所长，多传感器集成将是动态变形监测的发展趋势。近年来不少学者在研究桥梁、高层建筑等结构健康监测时，也同时安装了GPS和加速度计等多种传感器［6－8]，经消噪处理后运用振动分析理论从频率、振型、功率谱等结构动力学参数上去进行结构动力特性分析，而未对GPS与加速度计数据进行融合，以提高振动位移测量的精度、可靠性及采样率。为此，本文将利用Kalman滤波方法对GPS观测值和加速度计观测值进行集成，并讨论多速率与抗差的观测量随机模型。

1 集成GPS及加速度计观测值的Kalman滤波方法

Kalman滤波最优估计广泛应用于动态数据处理中，它是通过计算机实现的在时间域上的一个不断地预测、修正的递推过程，由于其在求解时不需要存储大量的观测数据，并且当得到新的观测数据时，可以计算得到新的滤波估计值。对于标准Kalman滤波的介绍，限于篇幅不再赘述其基本原理和公式，可以参考文献［9] 。

多传感器集成或融合就是通过一定的算法综合利用来自各个传感器的信息，以产生比单个传感器更准确、更可靠的信息。集成GPS位移观测值和高精度加速度计观测值，则是同时将GPS位移观测量和加速度计观测信息纳入滤波器观测方程中，增加观测信息，扩增设计矩阵和观测向量方程。当得到新的GPS观测值和加速度计观测值时，可以组成新的观测向量修正滤波模型预报信息。尤其当滤波系统存在较大的模型误差时，新的观测向量将更有效的约束和修正模型误差偏差，从而更准确的估计状态向量。若同时将监测点的位置、速度、加速度均视为状态向量，从而构造常加速度模型［10－11]，则滤波系统的运动状态方程和观测方程可以表示为:

2 多速率抗差模型

在高楼振动等动态监测实际应用中，单传感器可能会因为某些异常原因而导致其失效或者可靠性降低，如GPS观测中常由于受到周跳、多路径效应误差、信号中断和衍射误差等影响，而使得观测数据含有连续多个历元的粗差，或者观测值丢失等异常情况。针对观测值粗差处理，诸多学者提出了粗差探测和抗差估计等理论。其中，杨元喜院士等根据抗差估计思想，为抵制观测异常的影响，构造观测向量抗差等价权矩阵从而提出抗差Kalman滤波算法［12－13]。其中抗差等价权矩阵函数采用IGGⅢ方案，表示为:

假设各观测值独立，Pk为观测值Lk的抗差等价权矩阵…，pk(nk))，当观测值无粗差时，nk为在 tk历元时的观测值个数，式中为tk观测向量Lk中第i个观测值根据多余观测量计算的标准化残差，一般k0=1.0 ～1.5，k1=3.0 ～8.0。当监测点在 tk历元观测值即无多余观测且又可能存在异常时不能再根据观测向量的标准化残差来进行计算。而根据Kalman滤波中预测残差向量特征，改进如下:

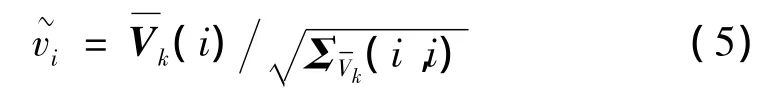
目前大地测量型GPS的数据采样率一般较低，要获取高楼的高频振动位移信息，需要更高的采样率。由于加速度计的采样率可高达100 Hz乃至1 000 Hz［8]，为了达到提高GPS采样率的目的，建立能够处理不同采样率观测值的数据处理方法，即多速率Kalman滤波方法［14]。

实质上，抗差Kalman滤波与多速率Kalman滤波的核心思想都是在特殊情况下，适当调整各观测量的权阵即随机模型而进行处理。假设各传感器之间相互独立，并假定各类传感器观测值噪声服从期望为0的正态高斯分布，对于不同类型的观测量，一般采用经验公式定权，则观测向量Lk的协方差矩阵为:

Kalman滤波过程包含状态预测过程和观测值更新过程。当GPS观测由于信号中断等原因而造成观测值丢失时，在观测数据更新阶段可以忽略GPS观测值对于状态估计值的贡献，即令GPS观测值的权P1=0，而仅利用加速度计观测值进行状态值的更新和修正，从而提高系统的容错性能和可靠性能。对于多速率滤波系统，假设GPS采样间隔为ΔTGPS，加速度计采样间隔为 ΔTacc= Δt，ΔTGPS/ΔTacc=M，M 为整数，在(k－1)ΔTGPS+mΔt时刻(m=1，2，…，M －1，k亦为整数)，由于仅存在加速度观测值而无GPS观测值，在滤波过程观测值更新阶段同理即可令GPS观测值的权为0，即综合模型预报信息和加速度计观测信息进行状态值的估计，从而达到提高系统采样率和不等采样间隔传感器集成的目的。

由上可见，对于观测值出现粗差、观测数据丢失、以及不同采样间隔的多速率滤波等均可以通过适当调整观测向量的权阵进而控制各观测量对于状态估计值的贡献而进行处理。

3 GPS振动位移测量试验

由于在实际高楼振动监测中，一般很难以精确知道振动的实际位移值，不利于实验的对照比较分析。为研究目的在下述振动台上进行试验以模拟高层建筑振动，其中振动台结构如图1所示，模拟振动监测试验的硬件配置如图2所示。该模拟振动台上可以安装GPS接收机和加速度计，通过与其相连的计算机中控制软件和驱动伺服马达用户可以控制振动台作水平面方向上各种不同频率和振幅的振动，并且可以输出其精确的实际振动位移值(精度为 0.1 mm)，以便与GPS测量结果进行对比，其它相关具体情况请参见文献［15] 。

图1 模拟振动台Fig.1 Simulated vibration table

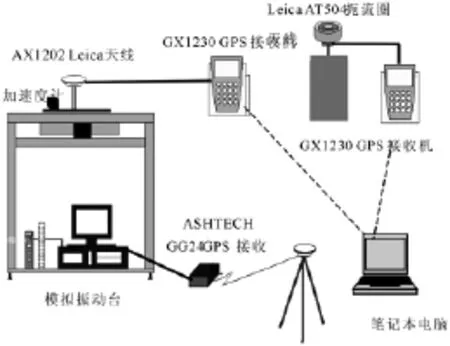
图2 模拟振动试验的硬件配置Fig.2 Hardware configuration for simulated vibration test

为简单起见，本次实验振动台仅在X方向以不同频率或振幅作余弦运动以模拟高层建筑振动。其中GPS采样率为20 Hz，X方向单轴敏感加速度计(型号:Honeywell QA－650)采样率亦为20 Hz。计算过程如下:首先，通过前一段时间的静态观测，进行基线向量解算;而后利用该基线先验信息，进行单历元解算(采用作者自主研发的精密动态变形监测数据处理软件GPSStructure Monitoring进行处理)，并通过坐标系转换(GPS测量坐标系为WGS－84)求得它们在平台坐标系中X方向振动坐标序列;最后，采用Kalman滤波方法对X方向坐标序列进行滤波处理，并与振动台输出的模拟振动理论值进行差值序列即残差序列比较，并且为对比分析集成加速度计的滤波处理效果采用下述两种方案进行滤波处理。方案一:仅考虑GPS观测值而不集成加速度计观测信息的的滤波方案;方案二:集成二者观测信息的Kalman滤波方案。由于本次实验是在香港科技园一很开阔地区进行以及采用的是Leica AT504扼流圈天线以抑制多路径效应影响，其多路径误差、信号遮挡、周跳影响等均比较弱，然而实际高楼监测应用中GPS观测值所受到的干扰影响可能比该实验严重很多。为了比较分析集成方法的滤波效果，在振幅为50 mm频率为0.25 Hz实验滤波前的GPS单历元解算坐标序列中，人为加上一些观测粗差和删减部分历元观测数据。其中在800(1)，1 600(3)，2 400(8)，3 200(10)历元处增加15 mm的粗差，4 000(10)历元处人为删除部分历元数据，括弧内数字表示连续设置增加粗差或者数据丢失的历元个数，以及方案一、二中滤波均采用抗差Kalman滤波算法。另一方面为验证多速率滤波的可行性，在下面的振动实验中均增加M=2、M=4时的两种多速率滤波处理方案。即假设GPS采样率仅为10 Hz、5 Hz，加速度计采样率为20Hz，为了提高监测系统的整体采样率达20 Hz，间隔均匀删去GPS观测值，而后采用上述多速率滤波方案进行处理。下面分别列出各不同振幅和频率的振动试验滤波效果图、RMS残差统计结果表。其中10 mm 0.25 Hz表示振动振幅为 10 mm、频率为 0.25 Hz，图 3至图4中，a子图表示滤波前坐标序列图;b子图表示实际坐标序列图，为了图形能够清晰表达a，b子图均只绘出前60 s坐标序列;c子图为未滤波之前的坐标残差序列图;d，e子图分别表示方案一，二滤波之后的坐标残差序列图;f，g子图分别表示M=2、M=4时的多速率滤波方法处理后的坐标序列残差图。

图3 25 mm0.25 Hz振动试验滤波效果图Fig.3 25 mm0.25 Hz filtering results of vibration simulation

图4 50 mm 0.25 Hz振动试验滤波效果图Fig.4 50 mm0.25 Hz filtering results of vibration simulation

表1中RMS残差计算公式如下:

式中，x表示测量值，可以为原始的或者滤波后的坐标值;xt为振动的真实坐标值;n为样本总数。

表1 RMS残差统计结果表(单位mm)Tab.1 Statistical results of RMS(mm)

由滤波效果图和误差统计结果表可以看出:

(1)从滤波前后对比来看，Kalman滤波方法对于高楼振动位移监测数据具有一定的去噪效果。从滤波方案一、二对比来看，运用Kalman滤波方法集成GPS和加速度计的方案二整体滤波效果要优于方案一，方案二由于充分利用了加速度传感器，集成了高精度的加速度观测值，即增加了观测信息和扩增了观测向量以及设计矩阵，从而能够更好的进行状态向量估计，提高位移观测量的精度。

(2)从图4中可以看出，滤波方案一中抗差算法对于粗差具有一定的抵抗作用，但是由于位移观测信息无多余观测且连续多个历元的粗差或者数据丢失影响，很大程度上降低了监测精度和可靠性。而集成方案中由于增加了另一传感器信息对于粗差和部分历元数据缺失的影响均有比较好的抵制效果，相比于在单传感器中可能由于某些原因而导致其失效或者可靠性降低，在多传感器集成中，综合利用各传感器信息，增加系统的抗粗差干扰性能和容错性能，从而提高系统的精度和可靠性。

(3)由图3，图4和表1可以看出，处理10 Hz，5 Hz采样率的GPS和20 Hz采样率的加速度计集成的多速率滤波方法取得比较理想的效果，从而在一定程度上弥补了GPS采样率采样不足的缺点，验证了不等间隔多速率Kalman滤波方法用于动态监测的可行性。

4 结论

利用Kalman滤波技术并建立合适观测量随机模型，可对GPS和加速度计两种传感器进行深度集成，充分发挥两种传感器的优点与作用，从而提高高楼振动位移监测的精度、可靠性和采样率。随着变形监测技术及传感器技术的发展，越来越多的传感器将用于动态变形监测，这些传感器各有其优点和缺点。如何对这些传感器进行深度集成，提高监测系统的监测精度及可靠性，并对不同传感器的监测数据进行融合与挖掘，将是动态变形监测的发展趋势。

［1] 黄声享，刘经南，柳响林.小波分析在高层建筑动态监测中的应用［J] .测绘学报，2003，32(2):153－157.

［2] 程朋根，熊助国，韩丽华，等.基于GPS技术的大型结构建筑物动态监测［J] .华东地质学院学报，2002，25(4):324－332.

［3] Lovse J W，Teskey W F，Lachapelle G，et al.Dynamic deformation monitoring of tall structures using GPStechnology［J] .Journal of Surveying Engineering，1995，121(1)，35－40.

［4] 贺志勇，吕中荣，陈伟欢，等.基于GPS的高耸结构动态特性监测［J] .振动与冲击，2009，28(4):14 －17，24.

［5] 伊廷华，张永恒，李宏男，等.多路径效应在GPS结构健康监测中的研究进展［J] .振动与冲击，2009，28(9):102－108，124.

［6] Chan W S，Xu Y L，Ding X L，et al.An integrated GPS-accelerometer data processing technique for structural deformation monitoring ［J] .Journal of Geodesy，2006，80(12):705－719.

［7] Li X，Ge L，Ambikairajah E，et al.Full-scale structure monitoring using an integrated GPS and accelerometer system［J] .GPSSolutions，2006，10:233 －247.

［8] Roberts G W，Meng X，Dodson A H.Integrating GPS and accelerometers to monitor the deflection of bridges［J] .Journal of Surveying Engineering，2004:65 －72.

［9] 杨元喜.自适应动态导航定位［M] .北京:测绘出版社，2006.

［10] Schwarz K P，Cannon M E，Wong R V C.A comparison of GPSkinematic models for the determination of position and velocity along a trajectory ［J] .Manuscripta Geodaetica，1989，14(5):345－353.

［11] 戴吾蛟，伍锡锈.变形监测中Kalman滤波状态模型的比较分析［J] .大地测量与地球动力学，2009，29(6):88 －92.

［12] 杨元喜.动态系统的抗差Kalman滤波［J] .郑州测绘学院学报，1997，14(2):79 －84.

［13] Yang Y，He H，Xu G.Adaptively robust filtering for kinematic geodetic positioning ［J] .Journal of Geodesy，2001，75(2):109－116.

［14] Smyth A，Wu M.Multi-rate Kalman filtering for the data fusion of displacement and acceleration response measurement in dynamic system monitoring［J] .Mechanical Systems and Signal Processing，2007，21(2):706 －723.

［15] 戴吾蛟，丁晓利，陈慧珊，等.不同环境下GPS用于水平振动位移测量的精度分析［J] .工程勘察，2007(11):59－63.