基于地面力学的月面巡视探测器动力学实时交互仿真研究

王 哲，高 峰，陈志伟，孙 鹏

(1.北京航空航天大学 交通科学与工程学院汽车工程系，北京 100191;2.GET集团北京分公司，北京 100190)

月面巡视探测器(即月球车)是探月工程的重要组成部分，构建三维虚拟交互仿真平台是其设计、优化及试验验证的有效手段，其中以地面力学为基础的动力学分析是开发的关键。基于动力学的仿真平台可同时具备沉浸性、自主性和交互性的特点，能够真实模拟探测器在深空环境中的巡视过程，研究人员可通过交互界面进行姿态控制、导航控制及遥操作等［1]。

随着虚拟样机技术的发展，近些年来国内外各深空探测研发机构均已展开了基于动力学分析的虚拟现实仿真研究。NASA JPL开发的实时仿真平台ROAMS［2](Rover Analysis，Modeling and Simulation)应用非线性Hunt-Crossley阻尼模型计算车轮－地面接触法向力，并基于土壤参数代替简易摩擦系数给出了地面附着力计算公式［3];加拿大MDA的Robert B等为欧洲航天局ESA的ExoMars探测车开发了多体动力学仿真工具RCAST(Rover Chassis Evaluation Tool)，应用轮土接触模块AS2TM(AESCO soft soil tyre model)进行了地面力学计算及试验研究［4];英国 Surrey空间中心Patel等开发的探测车移动性能评价系统RMPET(Rover Mobility Performance Evaluation Tool)，针对不同结构的探测器的挂钩牵引力进行了计算，同时对腿式机器人——地面作用进行了研究［5]。

尽管目前国内外分别针对虚拟现实仿真技术及轮土作用地面力学模型的研究成果颇丰，但将结合两者有效结合在同一实时交互仿真平台下的开发工作尚需进一步深入。其难点一方面在于松软土壤/月壤环境下轮土力学作用复杂，月壤模拟及各参数确定需要理论与试验综合分析;另一方面由于包含轮土细观作用的探测器整车动力学数学模型往往过于庞大，无法较好的实现与虚拟现实仿真工具的沉浸及融合。因此，探测器三维虚拟仿真平台的构建需要以试验结果为依据，在保证运算速度的情况下充分考虑模拟月壤变形及其对车轮滑转、沉陷和整车动力性的影响。通过利用动力学物理引擎，可自动、快速、有效的生成系统ODE及DAE方程组，从而加快开发进度。

鉴于以上原因，本文首先利用月面探测器移动性能土槽试验台进行了驱动轮牵引性能试验，针对车轮打滑下陷现象推导了基于滑转率的推土阻力修正模型。随后在Visual C++9.0平台下应用动力学物理引擎Vortex API进行编程建模，实现了基于推土阻力修正模型及Bekker理论的驱动轮和整车仿真，并结合试验数据进行了验证。最后给出了结论。

1 驱动轮牵引性能试验

1.1 土槽试验台概述

月面巡视探测器土槽试验台为满足行走机构地面验证试验需求而设计开发，为真实月面环境下车轮牵引性能预测提供基础和依据。其硬件部分包括土槽、台车、传动/加载装置、驱动控制电路和传感器系统。试验台可对车轮行驶速度、滑转率、轮上载荷等试验条件进行控制，其操作及传感器数据采集、处理和保存均由上位机程序和下位机程序实现。土槽试验台结构及控制流程见图 1［6]。

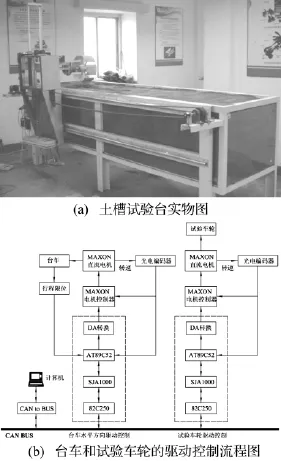
图1 土槽试验台实物图及其控制流程图Fig.1 Wheel-lunar soil interaction test-bed photo and drive control flow chart

土槽试验台试验用壤为北航汽车系基于与真实月壤具有相似矿物组成的吉林靖宇－辉南一带火山灰原料研制的BH－1模拟月壤。表1给出了压实整备后的槽内模拟月壤通过直剪试验得到的力学特性参数试验测量值［7]。

表1 试验用压实后模拟月壤参数测量值Tab.1 Measurements of compaction simulated lunar soil parameters

1.2 试验结果及分析

本试验中，试验轮为直径220 mm，宽度160 mm的刚性驱动轮，如图2所示。通过调整配重质量，控制车轮的垂直负载，以得到不同工况下车轮行走时产生的挂钩牵引力。为在一次试验中得到不同滑转率下的驱动轮牵引性能评价，采用了弹簧水平阻力加载装置获得变牵引载荷的方法。

图2 驱动轮土槽试验台牵引性能试验Fig.2 Traction performance test of driving wheel with test－ bed

车轮挂钩牵引力DP(Drawbar Pull)、驱动转矩T、车轮转速n、台车水平速度v及车轮垂直下陷量Zd可直接由传感器得到，滑转率s需要对直接测量值进行计算间接获得，即有:

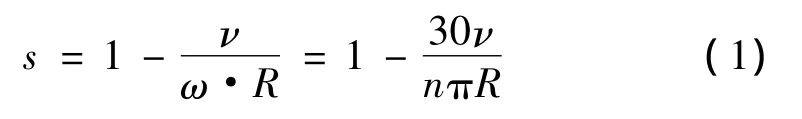
式(1)中，s为车轮的瞬时滑转率，v为台车的水平速度，n为车轮的实际转速，R为车轮的有效半径。

根据《月球探测二、三期工程总体论证初步技术要求》，月面巡视探测器设计质量M为200 kg，有效载荷为77 kg［8]。考虑月球重力加速度为地球的1/6，即1.62 m/s2，因此需要在土槽试验台设置约11.45 kg的负载。试验中通过调整配重质量，分别对负载为3.5 kg、8.0 kg、12.0 kg 及20.0 kg 四种工况进行了测试，车轮转速定为5.0 r/min。每次试验重复三次，分别得到挂钩牵引力DP、沉陷量Zd与滑转率s的变化历程曲线见图3及图4。

对比四种负载下的试验结果，能够看出负载的增大可获得更大的挂钩牵引力并带来更多的沉陷量。由图4可以看出，某一负载工况下的驱动轮沉陷量Zd与滑转率s可用线性关系来表示。当负载增大时，同时表现出最大沉陷量的增加及Zd-s曲线斜率的增加。由此说明滑转率增加使得车轮下陷速度变大，车轮严重打滑将加剧其沉陷现象，行驶阻力也随之增大。当滑转率增大为100%时，轮下模拟月壤出现剪切破坏后的大位移运动并形成流动滑移失效面，使得驱动轮失去附着力，无法继续前进。

图3 四种不同负载下的DP-s曲线Fig.3 DP-s curves of four different loads

图4 四种不同负载下的Zd-s曲线Fig.4 Zd-s curves of four different loads

2 基于滑转率的推土阻力修正模型推导

2.1 驱动轮行驶阻力定性分析

通过试验可以看到，基于滑转率的动态下陷为车轮沉陷的主要成分，决定着驱动轮能否具备更大的牵引能力。由车辆地面力学理论可知［9]，松软土壤下的驱动轮牵引性能主要由挂钩牵引力DP来评价，其值为驱动轮与土壤作用的附着力H与车轮移动时受到的合阻力Ff之差。合阻力Ff主要包括压实阻力Fr、推土阻力Ft及粘着阻力Fs。压实阻力Fr表现为驱动轮在运动过程中土壤被压实而形成轮辙或齿孔。推土阻力Ft指车轮沉陷时轮前隆起土壤被推移而产生的阻力，对软土环境来说，轮缘拥土现象往往不可避免，随着滑转率的增加会加大对DP的影响。粘着阻力Fs指松软土壤由于粘着作用附加在金属车轮上带来的阻力，在本试验中粘着多表现为颗粒间细观力作用，相对于前两者来说可忽略不计。以下重点针对压实阻力Fr及推土阻力Ft进行定量分析。

2.2 驱动轮行驶阻力定量分析

如图5所示，压实阻力Fr为σ(θ)的水平分量在θ1与θ2间的积分，即:

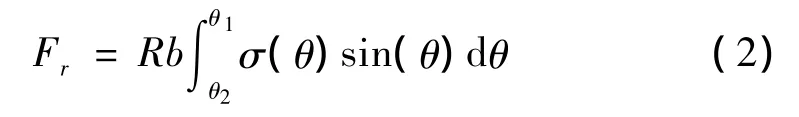
式中R为车轮半径，b为车轮宽度，σ(θ)为θ处的法向应力，θ1、θ2分别为车轮与地面接触时的接近角与离去角。推土阻力Ft的计算由图5所示几何关系，根据太沙基(Terzaghi)浅基础极限承载力 Flimit公式经过整理为［10]:

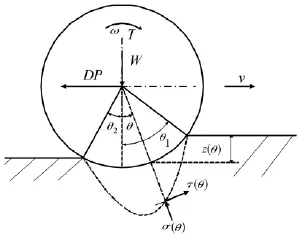
图5 驱动轮与月壤相互作用简图Fig.5 Driving wheel and the lunar soil interaction diagram

即:

其中bZd为作用面积，c为土壤内聚力，γ为土的容重，Nc、Nγ均为土壤内摩擦角φ的函数，可通过查表得到。对于易发生局部剪切破坏的松散土壤来说，太沙基Terzaghi通过降低 c和 φ值来对公式进行修正，即有［11]:

因此:

结合图4可知，某一负载下的沉陷量Zd可由沉陷量与滑转率的线性函数来表示。故设车轮静态下沉量为Z0，斜率为k0，可以得到:

因此基于滑转率的推土阻力修正模型为:

3 基于Vortex的巡视探测器驱动轮建模与仿真

3.1 动力学物理引擎Vortex

以Nasa利用Vortex开发FIDO火星探测器三维仿真平台为代表［12]，Vortex已成功应用于模拟操作训练、机器人远程控制仿真、高真实度地面车辆战场模拟及航天器在轨飞行和着陆器分析等方面。Vortex采用标准c++语言，以轴向包围盒法 AABB(axis-aligned bounding box)进行远场剔除，使用拉格朗日乘子法建立运动副和接触模型，应用LCP法进行动力学解算，在不失精度的基础上通过适当减少步进次数及建立松弛约束条件来保证实时性［13]。

图6所示为基于Vortex API构建月面巡视探测器仿真系统整体框架图。结合Vortex:Vx各类进行力元定义及动力学求解是本系统的特点。下面重点对其中的轮土交互作用部分进行分析。

图6 探测器仿真系统整体框架图Fig.6 Framework diagram of lunar rover simulation system

3.2 推土阻力修正模型下的动力学计算

根据地面力学的基本理论，采用被广泛应用的Bekker承压模型来描述月壤承压特性［9]，根据图5所示几何关系，其表达式为:

式中，σ为法向应力;z为下陷量;kc为土壤粘聚变形模量;kφ为土壤摩擦变形模量;n为土壤变形指数。根据J·Janosi剪切特性模型及摩尔库伦准则建立月壤剪切特性模型，有:

式中，τ、τmax为剪切应力及最大抗剪强度;K为土壤剪切变形模量;j为土壤与轮缘接触面的剪切位移;s为滑转率。由图5可得，车轮法向力W计算公式为:

挂钩牵引力DP为驱动轮与月壤作用的附着力H与合阻力Ff之差，即:

其中驱动轮附着力H为:

合阻力Ff为压实阻力Fr与推土阻力Ft之和，即:

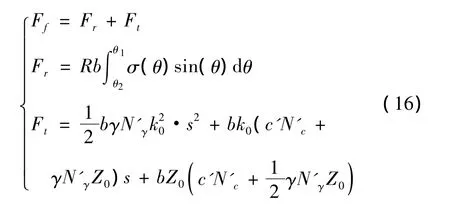
3.3 驱动轮仿真流程

取模拟月壤各参数试验测量值及推荐值如表2所示［10，14]。

表2 模拟月壤各参数测量值及推荐值(其中*为试验测量值)Tab.2 Simulated lunar soil measured parameters and recommended values(*indicate measured parameters)

驱动轮半径110 mm，轮宽160 mm。应用Creator生成三维场景模型(.flt)，并在 Vortex中创建驱动轮物理模型同时将三维地形模型可碰撞化，通过设置松软土壤属性参数定义月面，以进行车轮和地形的碰撞检测和相关动力学解算。初始化后系统实时获取三维场景中物理模型的轮土接触角 θ1、θ2。编程调用①描述Bekker模型的类Vx Pressure Sinkage Params Bekker;②描述软土地面力学剪切应力和剪切应变模型的类Vx Shearing Params Exponential;③描述运动副间的物理材料属性及摩擦运动设置、计算碰撞物体间的法向力、切向力的类VxContactProperties，积分求解 W、H、Fr、Ft，在一个帧显示周期内(60帧/秒)计算驱动轮下一步长的状态量，驱动三维场景模型完成帧显示，同时开始下一周期循环。图7为驱动轮Vortex仿真流程图，图8为沉陷仿真动画截图。

图8 模拟月壤下的驱动轮沉陷仿真Fig.8 Simulation of driving wheel in soft lunar soil

3.4 仿真结果与试验结果对比

基于土槽试验台试验的各个工况，分别进行了单轮变牵引载荷下的试验仿真模拟，并以牵引性能关键指标挂钩牵引力DP来对比仿真结果与试验结果的一致性。图9和图10分别给出了在负载3.5 kg/8.0 kg及12 kg/20 kg不同工况下DP－s仿真曲线。

图9 负载3.5 kg、8.0 kg下的 DP －s仿真曲线Fig.9 DP － s simulation curves of 3.5 kg and 8.0 kg loads

图10 负载12.0 kg、20.0 kg下的 DP －s仿真曲线Fig.10 DP-s simulation curves of 12.0 kg and 20.0 kg loads

其中，点圆线与虚线分别代表了试验数据95%的置信上线和置信下线，可以看出仿真结果基本落在了该置信区间中。尤其在高滑转率(s＞80%)时误差较小，说明了该模型能够较好的对车轮动态沉陷引起的牵引性能变化进行描述。

4 基于vortex的月面巡视探测器整车仿真

依据上述方法，同时对整车进行了建模和仿真。基于北航汽车系自主研发的月面巡视探测器样机结构图及参数［15](见图 11、表 3)，在 Creator下分别进行了整车建模和场景建模。为与设计内容一致，建模时四轮均定义为转向轮，分别由前后两个输入转向角控制，其铰接与约束拓扑结构如图12所示。

表3 月面巡视探测器结构参数Tab.3 Structural parameters of lunar rover

图11 月面巡视探测器结构简图Fig.11 Structural diagram of lunar rover

编程仿真中，分别定义了键盘“↑↓”键对整车进行加速、减速控制，“A、D”键控制前转向角，“← →”键控制后转向角;或通过shift+鼠标左键或右键单击对物体进行拖拽移动。初步实现了探测器在虚拟现实环境的巡游，仿真动画截图如图13所示。

图12 整车建模拓扑图Fig.12 Topology of lunar rover simulation model

图13 月面巡视探测器整车仿真动画截图Fig.13 Screenshot of lunar rover simulation animation

5 结论

本文通过土槽试验台驱动轮牵引性能试验得到了基于滑转率的沉陷量模型，并推导了松软模拟月壤环境下推土阻力修正模型。在VC9.0平台下，利用虚拟现实工具Vortex API进行了基于地面力学的驱动轮单轮牵引性动力学仿真，仿真结果与试验结果的对比验证了其一致性，尤其在滑转率大于80%的情况下该模型具有较好的精度。同时对自主研发的摇臂式探测器进行了整车建模，初步实现了软土环境下的实时交互仿真。本文的研究为开发模拟月壤下月面巡视探测器三维动力学仿真平台提供了有效方法。

［1] Kheddar A，Tzafestas K S，et al.Multi-robot teleoperation using direct human hand actions［J] .Advanced robotics，1998，11(8):799－825.

［2] Jain A，Balaram J，Cameron J，et al.Recent developments in the ROAMS planetary rover simulation environment［A] .IEEE Aerospace Conference［C] .Big Sky，Montana，2004:1－16.

［3] Sohl G，Jain A.Wheel-terrain contact modeling in the roams planetary rover simulation［A] .ASME international design engineering technical conference［C] .Long Beach，USA:DETC，2005:1－9.

［4] Robert B，Winnie L，Tim B.Development of a dynamic simulation tool for the Exo Mars rover［A] .ISA IRAS conference［C] .Munich，Germany，2005:1 －8.

［5] Patel N，Scott GP.Application of bekker theory for planetary exploration through wheeled，tracked and legged vehicle locomotion［A] . Space conference and exhibit［C] .California，2004:1 －8.

［6] 高 峰，孙 鹏，孙 刚，等.适用于行星探测车辆车轮移动性能测试的土槽装置［P] .中国发明专利:ZL200610076322.X.

［7] 孙 刚.月面巡视探测器行走机构通过性地面验证试验方法及装置研究［D] .北京:北京航空航天大学，2008.

［8] 国防科工委月球探测工程中心.月球探测二、三期工程总体论证初步技术要求［R] .2005.

［9] Bekker M G.Introduction to terrain-vehicle systems［M] .Michigan:The University of Michigan Press，1969.

［10] 邹 猛.月面探测车辆驱动轮牵引性能研究［D] .吉林:吉林大学，2008.

［11] Wong JY.Theory of ground vehicle［M] .John Wiley，1978:113.

［12] Melchior N A，Kwak JY.Particle RRT for path planning in very rough terrain［A] .NASA Science Technology Conference［C] ，2007.

［13] 龚 飘，刘子建，曾晓梅.虚拟环境中基于多体动力学的实时仿真［J] .计算机仿真，2004，6:96－99.

［14] Oravec H A.Understanding mechanical behavior of lunar soils for the study of vehicle mobility［D] .Ohio:Case Western Reserve University，2009.

［15] 崔 莹.可变直径轮月球车及关键技术研究［D] .北京:北京航空航天大学，2008.