金属热防护系统动力学建模研究①

王 亮，陈怀海，贺旭东

(飞器结构力学与控制教育部重点实验室，南京航空航天大学振动工程研究所，南京 210016)

0 引言

近年来，高超声速技术已从概念和原理探索阶段进入了以高超声速巡航导弹、运载火箭、跨大气层飞行器和空天飞机等为应用背景的先期技术开发阶段。高超飞行器在大气中飞行时，将遭受强烈的气动加热，这种气动加热对结构动力学特性的影响主要分为2个方面:一是温度场的不均匀分布，会造成热应力，使飞行器内部产生受拉或受压的效应，导致结构振动频率发生改变，尤其是温度场突然变化造成的热冲击，会诱导结构产生振动;二是温度变化直接改变结构弹性模量等物理特性参数，从而改变结构振动特性。

前人在研究温度场对结构动力学特性的影响时，均在假设结构温度场已知的条件下，计算其热模态，而未考虑热防护系统的建模及热力学响应分析。史晓鸣和杨炳渊［1］以变厚度板为研究对象，进行了热载状态下结构的瞬态温度场和振动特性分析。李增文等［2］使用热刚度计算理论，进行了不同温度场和不同结构材料的热颤振特性研究。通过热应力分析理论，获得结构在不同温度场作用下的热模态。王宏宏等［3］以变厚度导弹翼面模型为研究对象，通过有限元仿真，分析了加热状态下翼面模型的瞬态温度场和振动特性的变化过程，并与试验结果做了比较。Avsec和Oblak［4］研究了温度场对简支梁和悬臂梁振动影响，考虑了弹性模量、泊松比、线胀系数、剪切模量随温度的变化。结果表明，较小的温度变化，将导致梁振动频率发生较大变化。

现代的热防护系统研究中，金属热防护系统(Metallic Thermal Protection System，MTPS)是高超飞行器热防护系统的理想候选方案。目前，金属热防护系统的研究，主要集中在蜂窝夹层结构传热性能的优化［5－6］及中间纤维层传热的优化设计［7－8］，而缺乏金属热防护系统整体结构动力学特性的相关研究。范绪箕［9］叙述了蜂窝结构的传热计算的分层计算法、热网格法和有限元法，均无法作为动力学模型进行模态计算。因此，需对金属热防护系统动力学特性展开研究。

本文将金属热防护系统建模与结构热模态计算结合。给出金属热防护系统热力学和动力学建模，对表面覆盖金属热防护系统的结构进行热力学分析，并研究整体结构的热模态及其简化计算方法，探讨了温度对弹体结构弯曲模态的影响。

1 MTPS结构型式及材料选择

本文采用如图1所示的MTPS模型式［9］，外部面板采用Inconel 617的高温合金蜂窝夹芯结构，内部面板采用Ti15合金蜂窝夹芯结构，中间隔热层采用轻质低热导率的Saffil纤维隔热材料。内外金属蜂窝面板通过连接通道焊接，MTPS通过nomex应变隔离层与承力结构连接。

图1 MTPS模型式示意图Fig.1 Schematic diagram of the MTPS

由于一维热分析模型可满足初步的TPS热分析精度要求［10］，且MTPS各功能层材料的热物性参数随着温度变化是改变的。因此，该传热过程是瞬态非线性问题。导热微分方程描述如下:

式中 c(T)为比热容，J/(kg·K);k(T)为热导率，W/(m·K);T为温度，℃;t为时间，s。

2 蜂窝面外等效参数预测

金属热防护系统建模时，难以将所有蜂窝胞完全建立，因此考虑蜂窝面外参数等效，对其一体化建模。

2.1 蜂窝面外等效热参数确定

2.1.1 蜂窝面外等效热导率

一般忽略芯内的对流换热，也不考虑蜂窝芯侧壁的辐射换热。蜂窝芯内的传热可分为蜂窝芯材料的固体导热、封闭腔内的气体导热和上下两面板间的辐射换热3种方式。将3种传热的总热阻视为3个热阻并联，据此可算得蜂窝芯的当量热导率［11］:

等效热导率ke是蜂窝芯几何尺寸和材料热物性参数的函数。其中，kc为蜂窝胞壁材料的热导率，kg为蜂窝腔内气体的热导率，krad为蜂窝芯体辐射换热等效热导率，ƒ为密度百分比，即单位面积的蜂窝面板质量除以相同体积的金属质量，对于正六边形蜂窝，有ƒ=

空腔内气体导热的热导率:

式中 kg*为随温度而变的气体热导率;a为适应系数;γ为气体比热比;λ为气体分子平均自由行程;Pr为普朗特数，Lc=h为特征长度。

式中 Kb=1.38×10－23J/K，为波尔兹曼常数;dg为气体分子碰撞直径;p为蜂窝空腔内气体压强;T为空腔内气体的绝对温度。

上下两面板间的辐射换热等效热导率为

式中 σ为斯特藩波耳兹曼常数。

蜂窝内腔的统一的发射率ε由式(6)给出:

2.1.2 蜂窝面外等效比热容与密度

根据体积混合率原理，等效密度为

式中 ρc、Vc、ρg、Vg分别为蜂窝芯与腔内气体的密度与体积。

等效比热容为

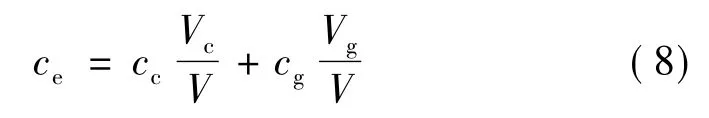
式中 cc、cg分别为蜂窝芯与腔内气体的比热容。

2.1.3 蜂窝面外等效热导率验证

以Inconel 617材料［12］的蜂窝结构为算例，考虑2种蜂窝胞的计算模型:

(1)腔内气体，蜂窝壁板分别建模;

(2)蜂窝使用等效参数进行整体建模。

正六边形蜂窝上下面板厚度为0.14 mm，壁厚度为0.14 mm，高度12 mm，边长为1.75 mm。设上面板1 000℃，其他部分的初始温度20℃，有限元计算得下面板温度结果如表1所示。从表1可看出，由于将3种热传导方式简化为一种，传热起始段2种建模方法误差较大，最大出现在第10 s，达到26.3%，但随后误差逐渐减小，从60 s开始，相同时刻2种方法得出右表面的温度基本一致，误差减小至5%以内，证明该简化方法用于长时间传热分析是可行的。

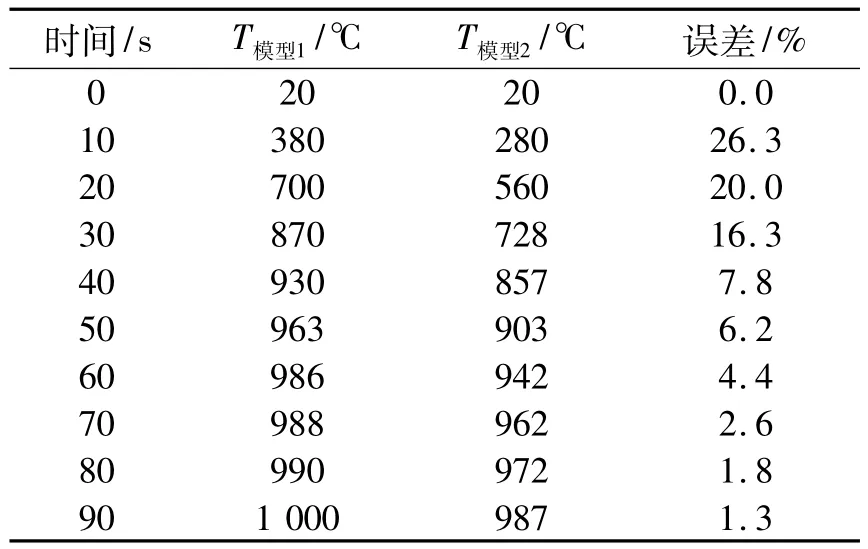
表1 2种计算模型各时刻下面板温度Table 1 Temperature of the lower panel fov two kinds of models at any time

2.2 蜂窝面外等效弹性系数

蜂窝壁厚t、蜂窝内切圆直径d及蜂窝层高度h。根据最小势能原理与最小余能原理，分别确定了金属蜂窝高度方向的等效剪切模量G23、G13与蜂窝材料的剪切模量Gs的关系式，又由体积混和律确定高度方向的弹性模量值E3与υ3，故蜂窝结构9个弹性参数的等效公式如式(8)所示［6］。

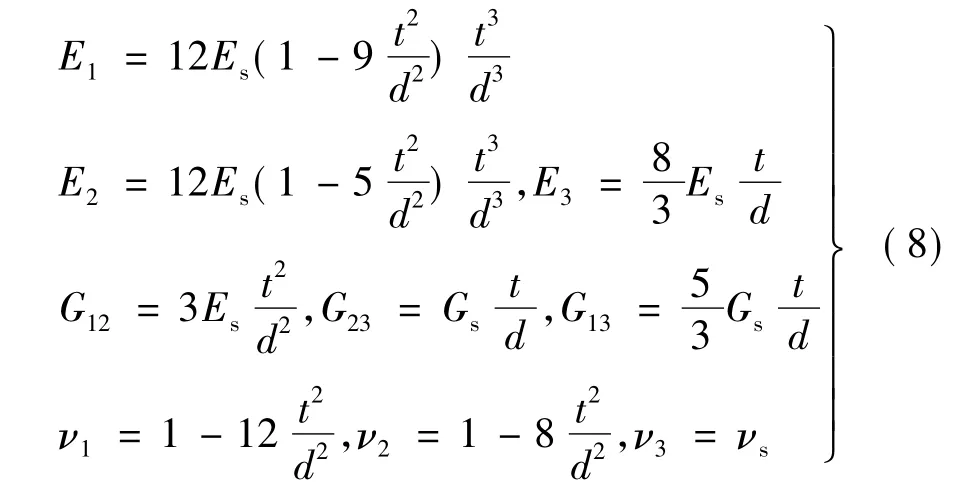
3 MTPS整体动力学建模与简化

考虑圆柱形的承力结构，横截面外直径400 mm，厚10 mm，长2 700 mm，MTPS块的面积为296 mm×196 mm，结构覆盖在承力结构表面，且各MTPS块间留有4 mm间隙，间隙由聚氨酯泡沫［13］填充。MTPS中内外蜂窝结构高度均为 12.28 mm，Saffil［14］隔热层与 Nomex［12］隔离层厚度分别为30 mm 和0.2 mm。整体模型如图2所示。其中，承力结构采用曲2D面建模，金属热防护系统采用3D实体建模。

图2 带MTPS的结构模型Fig.2 The structure model with MTPS

3.1 热力学响应

承力结构使用四边形单元划分，金属热防护系统各层结构采用六面体单元划分，热力学计算模型共408 240个自由度。当外表面施加1 000℃的温度载荷，初始温度20℃，使用 MSC.Nastran计算得时刻2 000、4 000、6 000、8 000、10 000 s时的温度场如图 3所示。从图3可见，从0～6 000 s，承力结构温度维持在20℃，从6 000 s才开始逐渐升高，在10 000 s时到达134℃。

3.2 热模态计算及简化

火箭等细长体结构，弯曲模态是主要模态，对导航与控制意义重大，直接影响飞行弹道与命中精度。因此，本文仅考虑模型在自由边界条件下的弯曲模态。

在计算结构的模态时，使用与上节相同的网格，模型的自由度数为210 924。由于自由度数较多，因此考虑以下的简化方法:将MTPS系统当作附加质量连接在承力结构上，计算热模态时，只需考虑承力结构的几何非线性与材料的物理非线性。通过以下方法算例验证简化方法的可靠性。

(1)将MTPS当作附加质量的简化模型A。此时，计算模型仅为承力结构的网格模型，自由度数为17 010。

(2)带有MTPS的未简化模型B。

图4和图5分别给出了常温下2种模型的前三阶弯曲模态。图6和图7分别给出了10 000 s时温度场下2种模型的前三阶弯曲模态。

图4 常温下简化模型前三阶弯曲模态Fig.4 The first three order bending modes of model A with room temperature

图5 常温下未简化模型前三阶弯曲模态Fig.5 The first three order bending modes of model B with room temperature

图6 10 000 s时简化模型前三阶弯曲模态Fig.6 The first three order bending modes of model A(t=10 000 s)

图7 10 000 s时未简化模型前三阶弯曲模态Fig.7 The first three order bending modes of model B(t=10 000 s)

根据以上所述计算结果，表2给出了各阶固有频率的比较。比较2种计算模型的计算结果，发现前三阶误差最大为6.45%，出现在常温模态的第三阶弯曲模态，从振型上看出，未简化模型中MTPS出现了局部模态，使得计算得到的对应的固有频率发生较大误差，而其他各阶的误差均小于5%，证明使用简化模型是可行的。因此，当分析模型的弯曲模态时，使用简化方法，不仅结果精度较高，而且节省计算时间。

表2 2种模型弯曲模态频率比较Table 2 Comparison of the bending modally frequencies between the two models Hz

同时发现，当施加温度载荷后，结构的固有振型基本不变，结构的前三阶弯曲频率都有所下降，而且变化均在4%以上，尤其是简化模型的第三阶变化达到了9%以上，下降超过50 Hz。原因是计算热模态时，需同时考虑材料的物理非线性与MTPS和承力结构的几何非线性。根据热弹性理论［15］，温度影响下的金属弹性模量可表示为

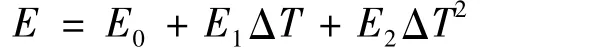
式中 E0、E1、E2是材料常数。

因此，温度升高材料的刚度会下降，导致固有频率下降。结构的几何非线性表现为当结构受热时，各部分将会发生热变形，即在温度作用下产生线应变。当结构各部分温度变化不均匀，或者存在外在约束或多个结构连接时，各结构在温度下伸缩不协调而相互抑制，热变形不能完全自由地涨缩，产生热应力。热应力的存在，改变结构的刚度分布，从而影响结构的动力学特性。因此，温度场对结构的模态具有较大影响，而影响的大小取决于结构的几何非线性与材料的物理非线性的共同作用效果。

4 结论

(1)给出了蜂窝结构面外的等效热传导系数、比热容、密度和弹性系数的数学表达式。算例结果表明，传热起始段2种建模方法误差较大，但随后误差逐渐减小，误差减小至5%以内。

(2)讨论了表面覆盖有金属热防护系统的承力结构的传热分析和弯曲模态分析，研究了2种建模方法(包括简化建模与非简化建模)对结构整体弯曲模态与固有频率的影响，提出了模型弯曲模态计算快速有效的算法。比较2种计算模型的计算结果，发现前三阶误差基本均小于5%，验证了简化方法。

(3)研究了结构的弯曲热模态，发现温度场对结构的模态具有较大影响。在10 000 s温度场下，结构的前三阶弯曲频率比常温下都有所降低，而且变化均在4%以上，尤其是简化模型的第三阶变化达到了9%以上，下降超过50 Hz。

［1］史晓鸣，杨炳渊.瞬态加热环境下变厚度板温度场及热模态分析［J］.计算机辅助工程，2006，15:15-18.

［2］李增文，林立军，关世义.超声速全动翼面热颤振特性分析［J］.战术导弹技术，2008(5):36-39.

［3］王宏宏，陈怀海，等.热效应对导弹翼面固有振动特性的影响［J］.振动、测试与诊断，2010，30(3):275-279.

［4］Jurij Avsec，Maks Oblak.Thermal vibrational analysis for simply supported beam and clamped beam［J］.Journal of Sound and vibration，2007，308(3-5):514-525.

［5］赵剑，谢宗蕻，张磊.高温合金热防护系统设计与分析［J］.宇航学报，2008，29(5):1679-1683.

［6］史丽萍，赫晓东，等.MTPS金属蜂窝夹芯结构尺寸效应的数值分析［J］.南京航空航天大学学报，2005，37(1):121-124.

［7］闫长海，孟松鹤，等.金属热防护系统多层隔热材料的稳态传热分析［J］.航空动力学报，2006，21(5):472-475.

［8］闫长海，孟松鹤，等.金属热防护系统纤维隔热材料的传热分析［J］.吉林大学学报(工学版)，2006，36(4):800-804.

［9］范绪箕.气动加热与热防护系统［M］.北京:科学出版社，2004.

［10］David E Myers，Carl J Martin，et al.Parametric weight comparison of advanced metallic，ceramic tile and ceramic blanket thermal protection systems［R］.NASA/TM-2000-210289.

［11］Robert T Swann，et al.Analysis of effective thermal conductivities of honey comb-core and corrugated-core sandwich panels［R］.NASA Technical Note D-714，1961.

［12］Mark P Gorton，John L Shideler，et al.Static and aero-thermal tests of a superalloy honeycomb prepackaged thermal protection system［R］.NASA Technical Paper 3257，1993.

［13］Design guide for use of last-a-foam fr-3700 for crash＆fire protection of radioactive material shipping containers［R］.General Plastics Mfg.Co.White Paper.

［14］袁政禾.“Saffil”氧化铝纤维的制造、性能及应用［J］.国外耐火材料，1995(7):10-16.

［15］Frostig Y，Thomsen O T.On the free vibration of sandwich panels with a transversely flexible and temperature-dependent core material［J］.Composites Science and Technology，2009，69(6):856-862.