真空绝热板纤维芯材等效热导率计算模型
2020-09-16于明志葛晨刘云苹胡静毛煜东
于明志葛晨刘云苹胡静毛煜东
(1.山东建筑大学 热能工程学院,山东 济南250101;2.南京市建筑设计研究院有限责任公司,江苏 南京210014)
0 引言
近年来,真空绝热板因低导热性已广泛地应用于保冷、保温等领域[1-2]。 真空绝热板的芯材种类主要有气凝胶—纤维复合材料和纯纤维材料(通常为叠层纤维)。 生产实践中发现,高真空条件下纯纤维芯材的热导率有时比气凝胶—纤维复合芯材的热导率更低,但是这种具有更低热导率纯纤维芯材的生产不够稳定性,因此亟需深入认识纯纤维芯材的传热机理,为提高生产工艺和产品性能稳定性提供理论依据和指导。
学者们对气凝胶以及气凝胶复合材料的研究已经比较深入[3-5],但对真空条件下纯纤维芯材导热性能的研究较少。 Zhao 等[6]采用修正的异常衍射理论,研究了纤维材料中辐射衰减系数的影响因素及变化规律。 何超等[7]、Xie 等[8]和方文振等[9]提出纤维等效结构的计算机生成法,基于生成的纤维结构求解了纤维增强气凝胶纤维复合材料的热导率。 夏德宏等[10-11]建立了纤维多孔介质热导率分形模型,分析了常压下孔隙面积、孔隙率分形维数和孔隙通道曲线分形维数等对其热导率的影响规律,并采用二值化阵列法计算热导率。 阚安康等[12]基于格子玻尔兹曼方法 LBM (Lattice Boltzmann Method)构建了纤维状芯材的等效结构,分析了热导率随着真空度的变化关系。 李辉等[13]采用有限元法建立碳纤维束微观结构模型,研究了纤维直径和间距对材料热导率的影响。 庞旭明等[14]利用最小热阻法和并串联模型建立了复合材料等效热导率计算模型。 聂荣华等[15]与陆思达等[16]分别采用等效热阻法、数值方法研究了结构参数对编织纤维材料等效热导率的影响规律。
上述研究中,有的等效热导率计算模型能较好描述材料的复杂结构,但计算工作量通常很大;有些模型对计算工作量要求不高,但通常只能计算结构较为简单的材料。 另外,目前关于真空条件下纤维导热性能的研究,大都只在较高温度时考虑热辐射作用,温度不高时则予以忽略。 但很多情况下真空绝热板的应用环境温度并不高(如建筑和冷储领域),在高真空条件下,芯材整体导热系数极低,此时热辐射作用通常不应忽略。 鉴于此,文章针对真空绝热板叠层纤维芯材,建立了能较好反映芯材复杂结构、计算比较简单、计算结果又较为准确的模型,并在此基础上分析了芯材导热性能影响因素及机理。
1 叠层纤维多孔材料结构模型
已有研究表明:纤维在垂直于热流方向排列时,其等效热导率最小[17],因此制备纤维芯材时应尽可能使纤维平行于芯材平面。 叠层纤维芯材结构的扫描电镜SEM(Scanning Electron Microscope)图如图1所示,可以看出绝大部分纤维直径近似相等,弯曲较少,可近似为等径直纤维;纤维沿厚度方向主要呈层铺结构,一层层叠合在一起,纤维可视为平行于芯材平面,而沿芯材平面方向(垂直于厚度方向)纤维则呈杂乱无章的随机分布。
为简化计算分析,根据SEM 分析结果,将纤维芯材结构简化为纤维为等径直纤维,并呈平行于芯材平面的一层层排列,每层厚度与纤维直径相等,且同一层内纤维呈随机布置,同层内不同纤维相交处为相接融合。 基于此假设,根据给定的纤维体积分数和直径等,采用计算机程序随机生成两个纤维层,其结构如图2 所示。

图1 叠层纤维结构的SEM 图

图2 随机生成的两层纤维分布示意图
2 叠层纤维材料等效热导率计算模型
由于纤维芯材内孔隙大都为微米量级,可忽略其内部对流传热[18],其等效热导率λeff由式(1)表示为

式中:λgs为纤维多孔材料中的气固耦合热导率,W/(m·K);λr为辐射热导率,W/(m·K)。
2.1 气固耦合热导率
由于叠层纤维各层厚度相同,层内纤维均呈随机布置,根据传热学和统计学基本原理可知,其相邻两层纤维的等效热导率与纤维芯材的有效热导率是相同的。
两个纤维层接触面处,会存在3 种接触形式(如图3 所示),即(1) 纤维层I 中的纤维与纤维层II 中的纤维接触,如图3(a)所示;(2) 纤维层I 中的纤维与纤维层II 孔隙中的气相接触(或反之),如图3(b)所示;(3) 两个纤维层气相接触,如图3(c)所示。 对于这3 种接触形式,两层纤维层间的热量传递方式分别为纤维到纤维的热量传递、纤维到气体的热量传递以及气体间的热量传递。 通过分析计算机生成的纤维结构,可以得到两层纤维间3 种传热方式的单元体在纤维层中所占的比例。

图3 相邻两个纤维层间的接触形式示意图
由于真空绝热板传热方向是沿厚度方向进行的,即热流传递方向为由纤维层I 到II,根据傅立叶定律可得到上述3 种传热形式的热导率。
纤维到纤维传热的热导率λff由式(2)表示为

式中:r为纤维半径,m;λf和λg分别为纤维块材和气相的热导率,W/(m·K)。
纤维到气体传热的热导率λfg由式(3)表示为
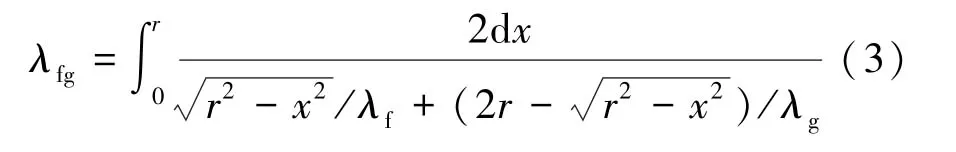
气相热导率λg为受限空间中的气相热导率,由式(4)[18]表示为

式中:λ0为大空间中静止气体热导率,W/(m·K);β为常数,取1.5;Kn为努森数,由式(5)表示为

式中:de为孔隙特征尺寸,m;L为气体分子平均自由程,由式(6)表示为

式中:KB为玻尔兹曼常数,KB=1.38×10-23J/K;T为温度,K;Pg为气相压力,Pa;dg为气相分子直径,m。
基于计算机生成的两层纤维结构,可以统计出其接触面间3 种接触形式分布占比,结合式(1)~(6),可以得到相邻纤维层间的气固耦合导热率λgs,由式(7)表示为

式中:a、b、c分别为纤维层间3 种接触方式分布的占比。
2.2 辐射热导率
由于纤维芯材厚度通常为厘米量级,满足光学厚近似,其辐射热导率λr由式(8)[19]表示为

式中:σ=5.67×10-8W/(m2·K4);ρt为纤维芯材的密度,kg/m3;Ke为平均衰减系数,由式(9)表示为

式中:fv为纤维体积分数。
分别计算出气固耦合热导率和辐射热导率后,代入式(1)即可得到纤维芯材的有效热导率。
3 结果与分析
3.1 模型的验证
为验证建立模型的有效性,利用文献[20]中的数据计算玻纤叠层纤维芯材随压强的变化关系,并将计算结果与其中的实验数据和模型计算数据进行对比。 温度为298 K、纤维直径为6 μm、纤维体积分数为5%时,压强对等热效率的影响如图4 所示,数据对比结果见表1。 可以看出,根据文章模型计算得到的结果比文献[20]模型计算结果更加接近其提供的实验数据。

图4 压强对等效热导率的影响图

表1 文章模型计算结果与文献[20]数据比较表
3.2 各参数对纤维芯材等效热导率的影响规律及机理
以玻璃纤维芯材为例,研究其等效热导率影响规律,并分析影响机理。 玻璃纤维块材密度2 600 kg/m3,则其纤维芯材密度ρt为块材密度与纤维体积分数的乘积,纤维热导率λf=1.1 W/(m·K)。
3.2.1 压强对等效热导率的影响
在温度为300 K、纤维体积分数为16%、纤维直径为6 μm 时,气固耦合热导率和芯材等效热导率随压强的变化如图5 所示。 随着压强的降低,等效热导率和气固耦合热导率先急剧下降,至100 Pa 时下降趋势逐渐变缓。 这是由于压强降低时,气体分子平均自由程变大,因此孔隙对气体分子运动的限制作用增强,即气体分子间的碰撞作用减弱,导致气相热导率下降,故芯材的等效热导率降低。

图5 压强对气固耦合热导率和等效热导率的影响图
3.2.2 纤维体积分数对等效热导率的影响
纤维直径为6 μm、压强为10 Pa 时,等效热导率随纤维体积分数的变化如图6 所示。 随着纤维体积分数的增加,等效热导率先减小后增加,存在最佳体积分数值使得等效热导率最小。 这是由于体积分数较小时,通过辐射传递的热量较多,占据主导地位。 随纤维体积分数的逐渐增大,纤维对辐射的遮蔽作用逐渐增加,使芯材等效热导率随辐射热导率的减小而减小;随着体积分数的继续增加,气固耦合热导率逐渐占据主导地位,因而体积分数增加,等效热导率随着气固耦合热导率的增加而增加。 由图6还可看出,最佳纤维体积分数随着温度的升高而增大,温度为253、300、323 K 时,其值分别为11%、13%和15%。

图6 纤维体积分数对等效热导率的影响图
3.2.3 温度对等效热导率的影响
压强为10 Pa、纤维直径为6 μm 时,气固耦合热导率、辐射热导率和等效热导率随的变化趋势如图7 所示。 当纤维体积分数低于某一数值时,同一体积分数下,温度越高,等效热导率越大。 这是由于体积分数较低时,辐射热导率占等效热导率份额较大(如图7(a)所示),因此温度升高时,辐射热导率增加量大于气固耦合热导率减少量,使等效热导率增大。 而体积分数较大时,温度越高,等效热导率将会越小,这是由于辐射热导率占等效热导率份额较小,几乎可以忽略,如图7(b)所示,由于此时气固耦合热导率受温度的影响更大,温度升高,气固耦合热导率减少量大于辐射热导率增加量,使得等效热导率减小。
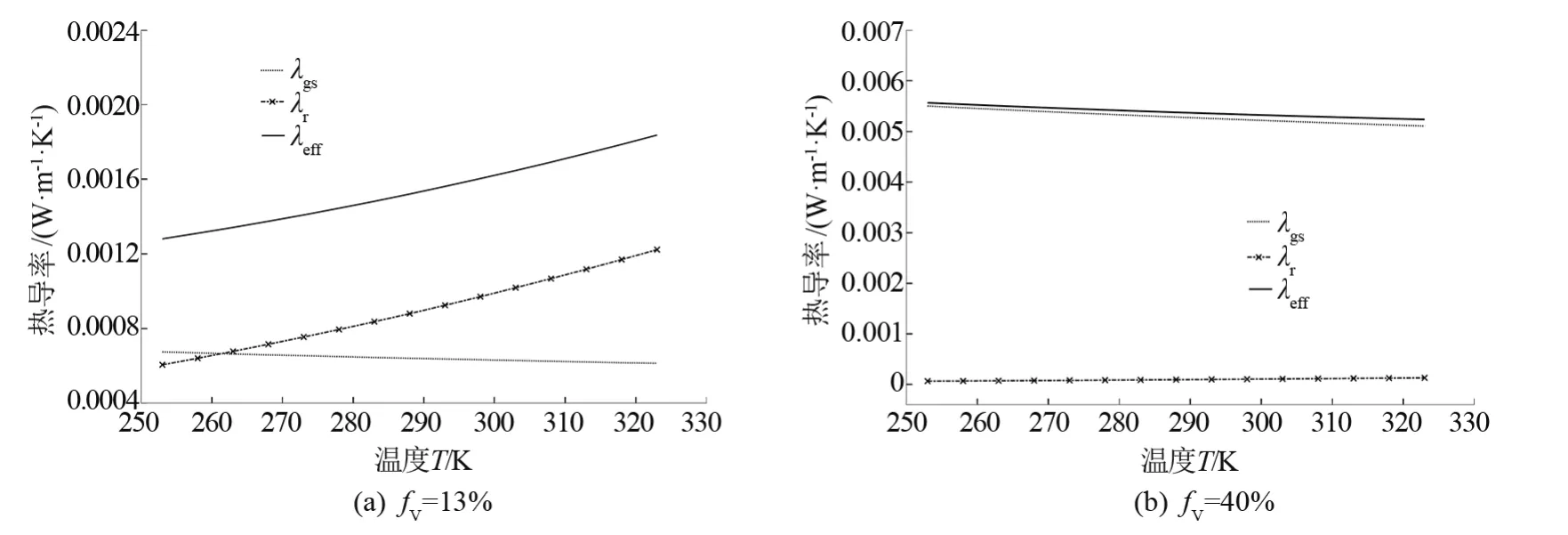
图7 温度对等效热导率的影响图

图8 纤维直径对热导率的影响图

图9 纤维直径对最佳体积分数的影响图
3.2.4 纤维直径对等效热导率和最佳体积分数的影响
温度为300 K、压强为10 Pa、纤维体积分数为13%时,气固耦合热导率、辐射热导率和等效热导率随纤维直径变化如图8 所示。 体积分数相同时,辐射热导率不随直径的变化而变化,气固耦合热导率随着纤维直径的减小而减小,使得等效热导率减小。体积分数不变时,直径的减小使得多孔材料孔隙尺度变小,由于温度和压强保持不变,所以气体分子平均自由程不变,由式(4)~(6)可知,孔隙尺寸变小则气相热导率变小,从而导致纤维芯材等效热导率减小。
温度为300 K、压强为10 Pa 时,最佳体积分数随纤维直径的变化如图9 所示。 纤维直径不同,最佳体积分数不同,最佳体积分数随着纤维直径增大而减小,纤维直径为2、12 和20 μm 时,最佳纤维体积分数分别为16%、13%和9%。
4 结论
基于叠层纤维结构电镜分析结果,建立了叠层纤维结构模型,在此基础上,利用傅里叶定律和分子运动论,建立了叠层纤维芯材等效热导率计算模型,并分析了等效热导率随纤维体积分数、直径、压强、温度等的变化规律及机理。 主要结论如下:
(1) 叠层纤维芯材的等效热导率随着纤维直径的减小和气相压强的降低而减小,当压强<100 Pa时,等效热导率随压强降低而减小的幅度趋缓。
(2) 叠层纤维芯材的等效热导率随纤维体积分数增呈非单性调变化,先减小后增大,存在使芯材等效热导率最小的最佳纤维体积分数,压强为10 Pa、纤维直径为6 μm,温度分别为253、300 和323 K时,最佳纤维体积分数分别为11%、13%和15%;最佳纤维体积分数随纤维的增大而减小,温度为300 K、压强为10 Pa,纤维直径分别为2、12 和20 μm时,最佳纤维体积分数分别为16%、13%和9%。
(3) 纤维体积分数较小时,叠层纤维芯材等效热导率随温度的增加而增加;当纤维体积分数较大时,叠层纤维芯材等效热导率随温度的增加而减小。
