一种适用于小推力轨控发动机“二次变轨”机动突防方案①

李红霞，李新其，，强洪夫，黄海平

(1.第二炮兵工程学院，西安 710025;2.96301部队，怀化 418008)

0 引言

利用地基动能拦截弹(ground based interceptor，GBI)在大气层外拦截远程弹道导弹的方案，是美国经过长时间研究的一种弹道导弹防御方案［1－2］。从20世纪70年代末，美国国防部开始研究第一代地基中段防御动能拦截弹技术开始，至克林顿政府在“国家导弹防御”的名义下开始发展第三代地基中段防御拦截弹技术为止，美国的“地基拦截弹”技术已经相对成熟［2－4］，对远程弹道导弹的生存能力构成的威胁也日益突出。发展具有自主突防能力的机动变轨突防技术，是应对反导防御系统日益增长的威胁的最佳突防技术手段。当前，对于弹道中段的机动突防，所设想的机动时机都选择在大气层外动能拦截器(EKV)的末制导段，因此成功突防对突防弹头机动过载的要求是很高的。国内外已有的研究成果表明［5－6］，突防弹成功突防所需的机动过载大约是EKV最大过载的一半，否则，选择在EKV末制导段内机动，只能算是无效机动。

考虑在目前发动机技术条件下，突防弹要想在弹道中段进行多次机动，那么轨控发动机的设计将不得不考虑采用液体发动机。这是因为液体发动机具有灵活控制推力大小和开/关机次数及工作时间较长等优点，从而能够满足弹道中段对多枚拦截弹进行机动规避的要求。然而，液体轨控发动机的推力较小，一般为几百牛顿，如果弹头质量达到1 t，轨控推力产生的最大机动加速度只能在0.1～1.0 m/s2。显然，凭借如此小的机动加速度，想在EKV末制导段实现以比拼机动性能为特点的变轨突防，是不现实的。在此种背景下，迫切需要研究与实际机动性能相符的机动突防技术。

本文在分析反导拦截系统固有战术、技术性能弱点基础上，提出避开EKV机动性能最强的末制导段，而在EKV自由飞行段和末制导结束后分别实施“二次机动”的规避突防方案，旨在解决突防弹成功突防所需的机动过载、脱靶量和落点偏差满足战略导弹突防作战的战术、技术要求。

1 弹道中段“二次变轨”机动方案的描述

1.1 对EKV拦截作战的战术、技术性能弱点分析

通过分析文献［7－12］，对EKV拦截作战性能弱点归纳如下:

(1)EKV对目标的探测距离有限。EKV和助推器分离后，在末制导段只能依靠自身的探测设备对目标弹头进行探测，探测距离仅数百公里。在EKV无法实时探测到目标相对距离信息的情况下，只能依靠此前对目标当前飞行信息的估计来维持自身的飞行状态。如果突防弹头在EKV视线距离以外实施某种机动，EKV是无法及时获取目标状态信息的，也就无法及时引导自身校正飞行状态。

(2)EKV的持续机动能力有限。目前飞行器的轨控发动机主要有液体燃料发动机和固体燃料发动机。前者推力较小，可控制推力的大小并灵活开关机，可多次使用;后者推力大，但其推力的大小和持续时间不可控，发动机工作时间短，且只能一次性使用。由于EKV采用固体燃料发动机，持续工作时间短，故EKV在末制导段的最大可机动能力是很有限的，约为1 000 m。

(3)EKV长达数分钟的无控飞行给突防弹头实施机动突防提供很好的机会。EKV与助推火箭分离后，即进入无控飞行阶段，此时EKV仅受重力作用。EKV进入无控飞行之前，GBI为保证对目标具有较高的拦截成功率，已将EKV送入了零控拦截弹道，因此只要进攻弹不改变飞行状态，就可实现成功拦截。但当进攻导弹进行变轨机动时，EKV受发动机可持续工作时间限制和EKV红外导引头探测视场有限等条件限制，无法相应进行变轨机动，这给突防弹头利用EKV的无控飞行阶段实施变轨机动规避提供了良好的机会。

1.2 突防弹“二次变轨”规避突防原理

突防弹头实施2次机动变轨的规避突防策略是指为突破同一枚EKV的拦截，突防弹头在EKV自由飞行段和末制导段结束后分别进行1次变轨机动。第1次变轨机动是利用EKV对目标的探测距离有限的技术缺陷，以较小燃料消耗达到足够大的零控脱靶量;二次机动是利用EKV固体燃料发动机可持续工作时间较短，发动机一旦使用将无法再次开机的缺陷，在EKV发动机燃料耗尽之后，再次处于无控飞行状态情况时，突防弹头进行第2次机动，产生达到规定要求的脱靶量，并通过对突防弹头机动方向等轨控发动机参数的优化设计来修正第1次机动规避引起的落点偏差。

“二次变轨”规避突防方案的原理如图1所示。

图1 EKV与突防弹头相对位置关系图Fig.1 Relative position of EKV and penetration warhead

图1中p1点是突防弹头如果不机动，沿原弹道mp1飞行时，必将会被EKV拦截的点。m点是突防弹头在EKV自由段飞行开始时实施的机动变轨位置，经过数分钟的无控飞行后，到达B点。被EKV在i处探测到，EKV估算出如果继续沿原弹道飞行，将产生Rmiss－1的脱靶量。为了消除这个因突防弹头在EKV自由飞行内机动引起的零控脱靶量，EKV需要采用末制导来实现。EKV的末制导主要控制轨控发动机的开机时间和推力方向，本文主要分析脱靶量 Rmiss－1对EKV轨控发动机开机时刻的影响。

一般情况下，即Rmiss－1小于EKV最大机动距离时，对于EKV而言，由于轨控发动机点火之后无法进行再次点火，为防止在EKV轨控发动机停止工作之后，突防弹头会利用碰撞拦截之前EKV又将处于无控飞行状态而再次实施变轨机动，故EKV应尽量把轨控发动机关机之后至拦截之前的剩余飞行时间压缩至最短。因此，EKV会在耗尽关机之前拦截机动中的突防弹。

当Rmiss－1大于EKV最大机动距离的情况下，EKV仅靠末制导段的机动是无法完全消除Rmiss－1的，要消除剩下的零控脱靶量偏差，只能靠EKV末制导结束后的剩余飞行时间来解决。这就为突防弹成功突防提供了一个时间窗口。

令EKV的机动加速度为aI，EKV轨控发动机的最大持续工作时间为ΔTmax，剩余飞行时间为tIs，则tIs与Rmiss－1的关系如下:

显然，由突防弹头在EKV自由飞行段因机动引起的 Rmiss－1越大，tIs就越大;而 tIs越大，突防弹头所能产生的脱靶量就越大。

1.3 “二次变轨”突防中的落点偏差的修正

每次机动都会产生相应的落点偏差，“二次变轨”突防对落点偏差的控制是用第2次机动所产生的落点偏差来修正前一次机动的落点偏差。可用图2所示的突防弹机动引起的落点偏差示意图来说明其思路。

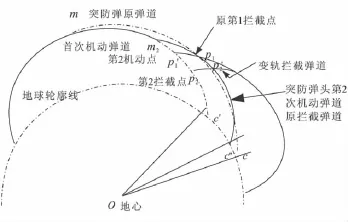
图2 突防弹机动引起的落点偏差示意图Fig.2 Fall point windage brought by penetration missile maneuver

图2中c点是突防弹不机动时的落点(不考虑突防弹的再入机动)，拦截系统选择p1点作为第1拦截点;m点为突防弹的第1次机动点，m点的地心矢径令为rm，突防弹首次机动后产生的零控脱靶量为，机动后的落点为c'，c'与原落点c之间的纵向落点偏差为ΔLmc，横向偏差为ΔHmc。EKV在末制导段选择突防弹机动后新弹道上的p2点作为第2个拦截点;突防弹在EKV末制导结束后于m2点处实施新的机动变轨，m2点处的地心矢径令为rm2，突防弹第2次机动后产生的脱靶量为，机动后的落点为 c″，c″与 c'之间的纵向落点偏差为 ΔLm2c'，横向偏差为 ΔHm2c'。为此，只要 c″与原弹道落点c之间的落点偏差能够控制在可容许的落点偏差阈值ΔΓ内就能满足突防规避参数设计对落点精度的要求。

ΔLm2c'与ΔHm2c'的产生必须满足约束条件:

2 机动规避参数的综合规划模型

突防弹头机动规避的轨道优化参数包括:发动机燃料质量秒耗量、推力作用方向和作用时间。显然，应以发动机燃料消耗量最小为优化指标;而约束条件则是指机动后产生的突防脱靶量和落点精度要求。令突防弹在EKV与助推火箭分离后立即实施机动，第1次机动持续时间为t1;第2次开始时间发生在EKV轨控发动机熄火之后，令第2次机动的持续时间为t2。且令突防发动机推力为PM，第1次机动突防发动机推力方向与射击平面的夹角为σmt1，推力在射击平面内的投影与ox的夹角为θmt1;第2次机动推力方向与射击平面的夹角为σmt2，推力在射击平面内的投影与ox的夹角为 θmt2。显然，t1、t2、σmt1、θmt1、σmt2和 θmt2就是待优化的轨控发动机的参数。

根据以上分析可以很容易建立其优化模型。

目标函数:

使J最小的终端约束条件:

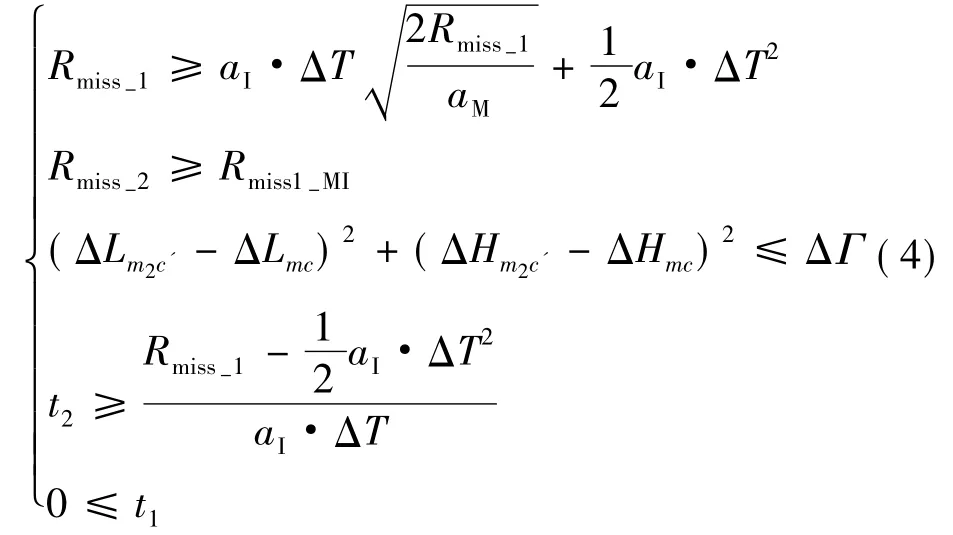
其中，ΔΓ≤(1+20%)·ε(3σ)。

导弹质量变化方程:

式中 ε(3σ)表示精度;m0为突防弹开始机动时的初始质量;m'为发动机燃料秒流量。

3 基于遗传算法的突防规划决策算法

考虑遗传算法具有通用性、鲁棒性及全局最优性等优点，适用于处理传统搜索方法难以解决的复杂非线性问题，因而采用遗传算法设计以上优化模型的算法。本文需要解决的优化问题具有较多约束条件，因此在算法的设计中引入惩罚函数方法，并通过动态改变算法参数来改进优化的收敛性。

本文求解的是最小值问题，故目标函数值越小，其适应度越好，所以适应度函数取为

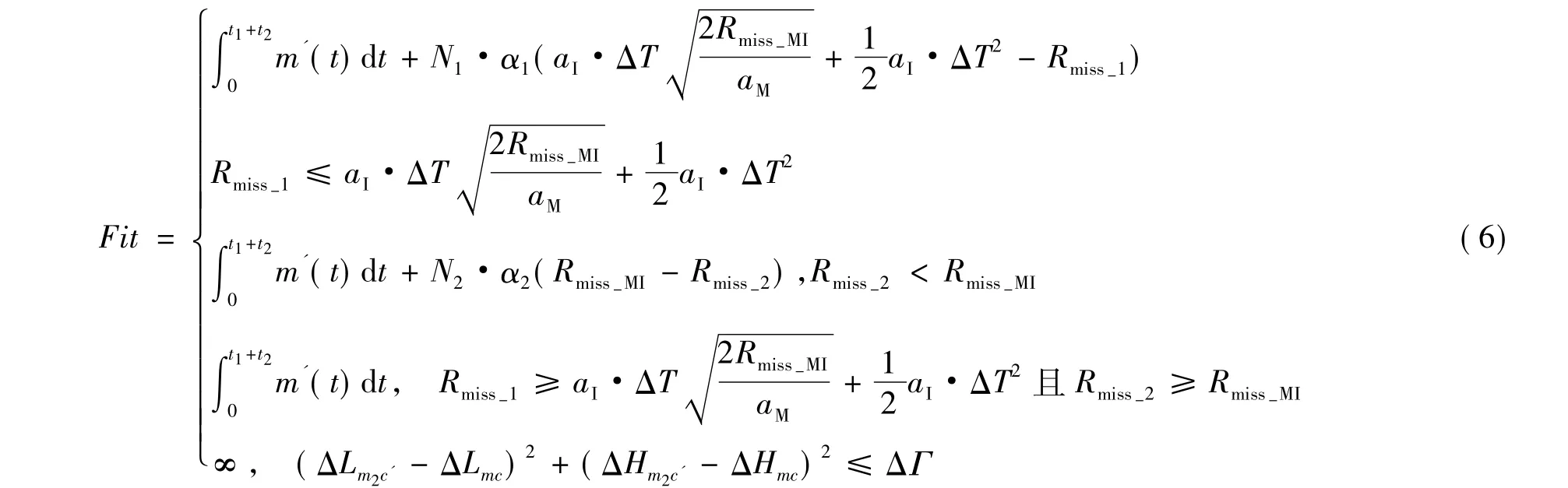
其中，α(Rmiss－0－ Rmiss)为惩罚函数:

4 仿真结果与分析

4.1 仿真初始参数的设定

假设突防弹在头体分离后不久，部署于目标点附近的导弹拦截系统的GBI拦截弹在预警系统的支持下开始准备起飞拦截，EKV与助推火箭分离时刻即为对抗开始时间。突防弹与EKV初始运动参数设定见表1。EKV在沿零控拦截流形弹道飞行479.03 s后，将对突防弹头实施准确拦截，其原拦截点数据如表2所示。

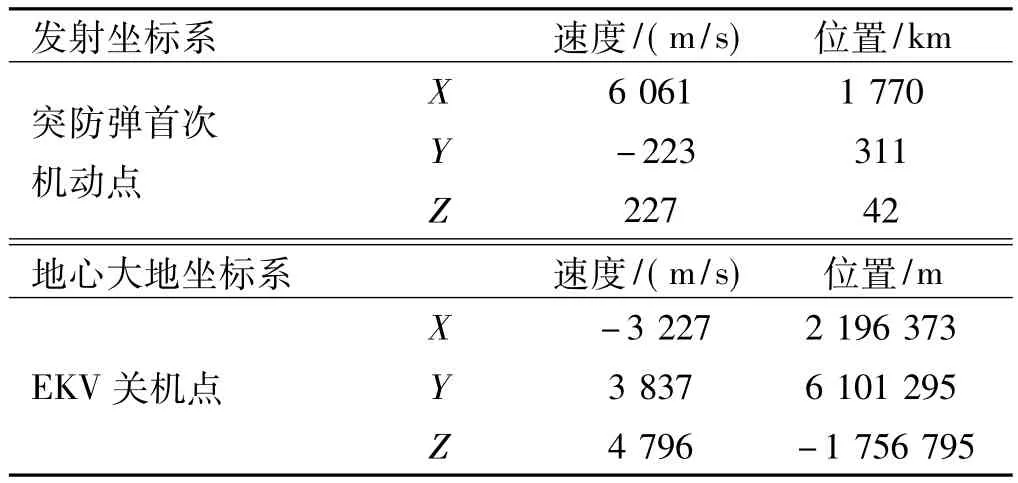
表1 突防弹/EKV初始运动参数Table 1 Initial motor parameters of penetration missile/EKV

表2 EKV零控拦截初始参数Table 2 Initial parameters of EKV zero-control interception

根据突防弹头二次机动规避的原理，知突防弹头进行机动规避时，需要控制的参数主要是每次机动的持续时间和机动方向(机动方向包含有2个决策参数)，共6个主要参数。在进行突防弹头机动规避参数优化设计时，本文将分二阶段进行。

4.2 突防弹头第一次机动轨控参数控制仿真

令突防弹头的机动加速度为aM，EKV的最大机动加速度为aI，EKV的最大机动时间为Δt，成功突防所需要的脱靶量为Rmiss－MI，则突防弹头第1次机动需要产生的零控脱靶量计算公式为

这里，突防弹头的最大机动加速度取0.3 m/s2，EKV最大机动过载取为4 gn，EKV的最大机动时间取为7 s。采用本文所建立的基于遗传算法的突防弹头机动参数最优控制模型来编程计算，获得突防弹头要达到所需零控脱靶量时，第1次机动持续时间、轨控发动机推力与射击平面偏角、轨控发动机推力在射击平面内投影与发射系X轴倾角3个控制参数的满意解。

突防弹头第1次机动持续时间及产生的零控脱靶量与遗传代数关系如图3所示。从图3可以看出，当遗传进化至第100代时机动持续时间和因此而产生的零控脱靶量都能实现较好的收敛。计算表明，突防弹头第1次机动所需要持续时间为:14.65 s，产生的零控脱靶量3 202.98 m，符合突防弹头机动规避的控制要求，这验证了利用遗传算法求解该问题的有效性。

突防弹头的机动方向的优化结果见图4和图5。

多次计算表明，突防弹头推力在射击平面的投影与X轴之夹角θP1大概在±(90±10)°之间变动，突防弹头推力方向与射击平面所成夹角σP1则在(0±6)°之间变动。这里 σP1= － 2.862°，θP1= － 95.63°。产生的纵向落点偏差为20 139.67 m，横向落点偏差为10.45 m。

4.3 突防弹头第2次机动轨控参数控制仿真

突防弹头第2次机动时轨控发动机的3个控制参数:机动持续时间tjM2、轨控发动机推力在弹道平面内的投影与突防弹发射系X轴的倾角(θPM2)和发动机推力与弹道平面的偏角(σPM2)。在计算轨控参数的最优值时，需确定EKV末制导段机动时刻。在此假设EKV选择在905.046 3 s时实施第2次拦截，经计算，其脱靶量为0.041 m。

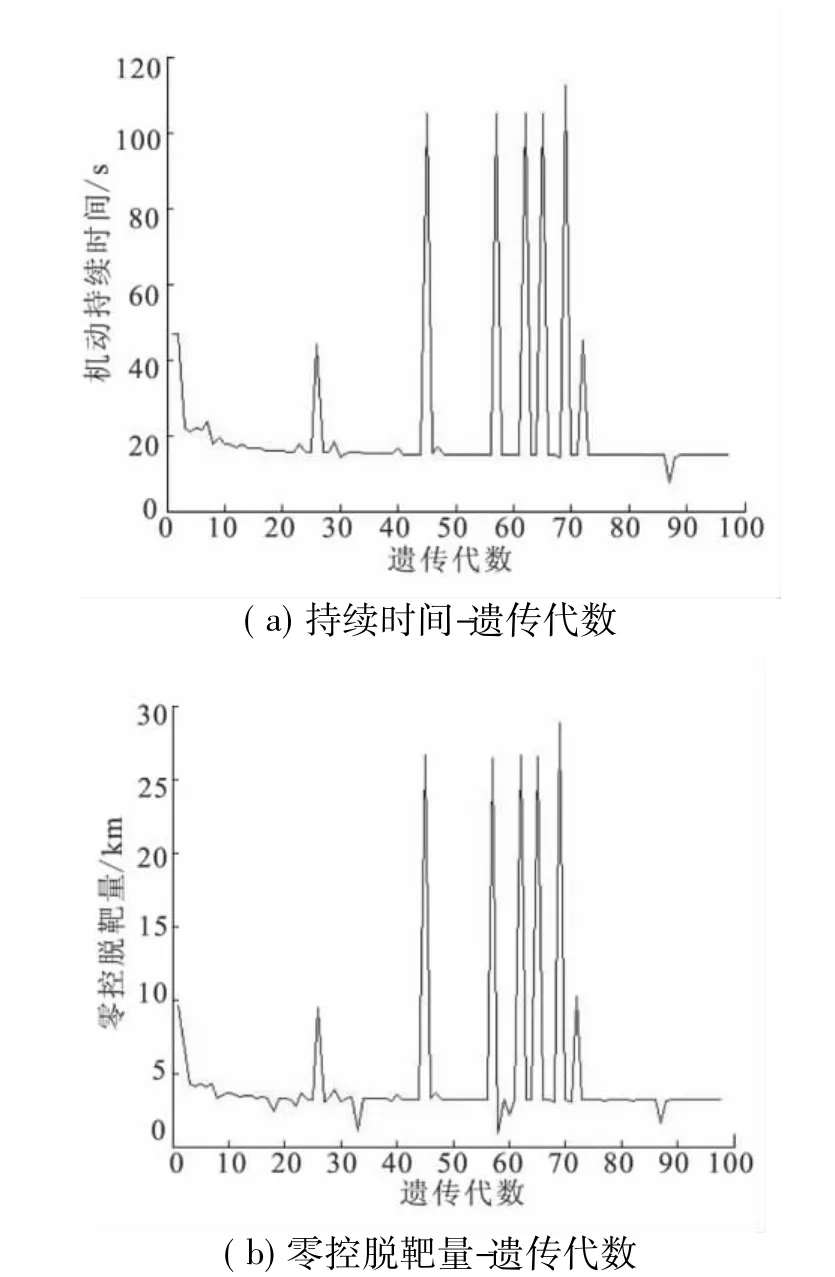
图3 突防弹头第1次机动持续时间及产生的零控脱靶量与遗传代数关系图Fig.3 Relation of duration time and zero-control undershoot capacity brought of the first maneuver of penetration warhead and inherited algebra

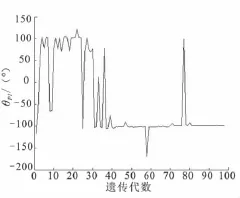
图4 突防弹头推力在射击平面的投影与X轴之夹角θP1与遗传代数关系图Fig.4 Relation of angle θP1by X axis and projection of penetrationwarhead thrust in fire planeand inherited algebra

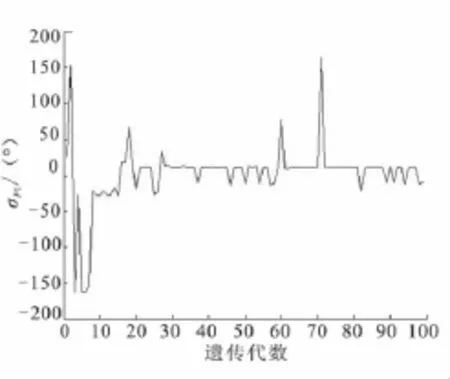
图5 突防弹头推力方向与射击平面所成夹角σP1与遗传代数关系图Fig.5 Relation of angle σP1by fire plane and thrust direction ofpenetration warhead and inherited algebra

图6 机动持续时间tjM2、推力方向σPM2及θPM2随遗传代数变化关系图Fig.6 Relation of tjM2，σPM2and θPM2changing with inherited algebra

仍采用遗传算法计算突防弹头第2次机动时的轨控参数，优化结果见图6。突防弹头第2次机动产生的脱靶量及综合落点偏差的优化结果如图7和图8所示。从图6～图8可看出，决定突防弹头第2次机动弹道的3个主要控制参数:发动机持续工作时间tjM2、轨控发动机推力倾角θPM2和推力偏角σPM2在遗传至第100代时都能实现较好收敛。2个约束条件:成功突防所需的脱靶量和落点精度要求也都能较好的实现。其中，突防弹头的机动持续时间为11.679 s，轨控发动机推力的 θPM2= －3.356 4°，σPM2= －51.555°，产生的脱靶量为19.439 m，前后2次机动形成的综合落点偏差为997.43 m，落点偏差增加量控制在原弹着点散布精度的0.25范围内，从而证明遗传算法能够有效解决突防弹头轨控发动机的优化控制问题。

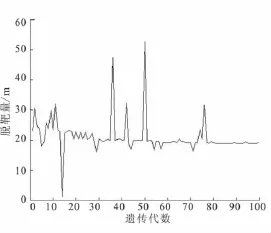
图7 突防弹头第2次机动产生的脱靶量与遗传代数关系图Fig.7 Relation of zero-control undershoot capacity brought by the second maneuver of penetration warhead and inherited algebra

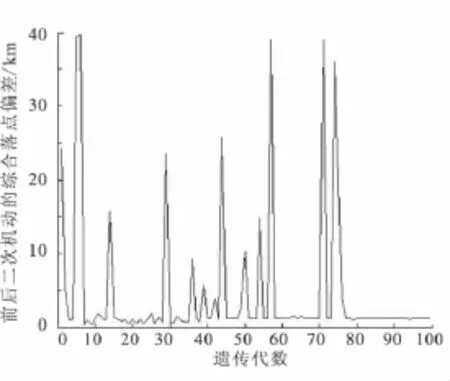
图8 突防弹头前后2次机动形成的综合落点偏差与遗传代数关系图Fig.8 Relation of synthetic fall point windage brought by two maneuvers of penetration warhead and inherited algebra

5 结论

(1)突防弹进行“2次机动”的小推力机动规避突防能达到成功突防所需的脱靶量要求，能够实现对机动引起的落点偏差的纠正，二次机动所需的轨控发动机累计机动时间不超过26.33 s，最终产生的脱靶量达到了19.439 m，满足导弹突防作战的战、技术要求。

(2)“2次机动”规避突防显著降低了成功突防所需的机动过载。突防弹头的最大机动加速度取为0.3 m/s2，能够实现突防，突防所需的机动过载降低了1个数量级以上。

(3)利用遗传算法进行突防弹头轨控发动机控制参数的优化设计是有效的。进化算法能够解决突防导弹在EKV自由飞行和末制导结束段2个阶段内轨控发动机工作时间、机动方向等6个机动弹道控制变量的优化设计问题，实现战术要求的脱靶量和落点精度，较好地满足突防弹头轨控发动机优化控制的智能决策要求。

［1］董汉权，陆铭华.针对国家导弹防御系统突防措施研究［J］.现代防御技，2004，32(3):15-18.

［2］Brett Newman.Exo-atmospheric intercepts using zero effort miss steering for midcourse guidance［C］//Proceedings of the AAS/AIAA Spaceflight Mechanics Meeting.Pasadena，CA:AIAA，1993:415-433.

［3］Daniel B，McAllister.Planning with imperfect information:interceptor assignment［R］.C104-1816，5.Jul.06.

［4］Kubilay Uzun.Requirements and limitations of boost-phase ballistic missile intercept systems［R］.0704-0188，Monterey:Center for Joint Services Electronic Warfare Naval Postgraduate School，2004.

［5］Paul Zarchan.Tactical and strategic missile guidance［M］.AIAA Tactical Missile Series，Vol.124.

［6］李新其.弹道导弹突防规划与控制研究［D］.西安:第二炮兵工程学院，2010.

［7］Midcourse Missile Defenses Advance on Interceptor Fronts［N］.Aerospace Daily，2003-8-19.

［8］MDA Test Flies Orbital Sciences Booster for GMD Program［N］.Defense Daily，2003-8-19.

［9］陈义光.美国国家导弹防御系统与俄罗斯的应对措施［J］.导弹与航天运载技术，2001(4):54-60

［10］POSTOL TA.Why missile defense won＇t work［EB/OL］.［2005-05-02］.http://www.Pbs.org/.

［11］Full scale exoatmospheric kill vehicle［EB/OL］.［2005-05-02］.http://www.Ammodel.Com/.

［12］赵秀娜.机动弹头的智能规避策略研究［D］.国防科学技术大学，2006.