穿越文化隧道 赏析中考试题

243000 安徽省马鞍山市成功学校 范宏业

穿越文化隧道 赏析中考试题

243000 安徽省马鞍山市成功学校 范宏业

在《义务教育数学课程标准》中,“数学是人类的一种文化,它的内容、思想、方法和语言是现代文明的重要组成部分”.也就是说,数学教育,不仅是教学生基本的数学内容和解答数学题目,而且还要将教学内容涉及的文化部分要从隐性状态转化为显性状态,这就需要广大教师在教学中注意挖掘教材隐藏的文化现象,通过恰当的方式传授给学生,从而“促进学生全面、持续、和谐地发展.”当然,这不仅仅可以在教学环节中实施,而且可以在中考命题环节实施,从而更好地发挥中考试题的正面的导向作用.

1 “勾股文化”,灿烂夺目

千古第一定理——勾股定理,是中考命题的永恒话题.在每年中考中,都会有一些新颖别致的试题,今年也不例外.

例1 (2011年台山)如图1,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用X,Y表示直角三角形的两直角边(X＞Y),请观察图案,指出以下关系式中不正确的是

图1

2 七巧板,新作为

图2

七巧板是中国传统玩具之一,七巧板除“七巧板”的名称外,还有不少名称：“益智图”、“智慧板”、“唐图”等都是七巧板的别称.它起源自宋朝的“燕几图”,经过明清两代的发展,逐渐演变成现在的结构.

七巧板对思维力、想象力、图形分析、创意逻辑等方面有很大的促进作用,是开发智力、锻炼思维的一种好工具.它的制作及玩法都很简单,只须按图示剪出七块图形,然后拼出各类图案即可.因此,七巧板也成为命题专家们的选材对象.

例3 (2011年温州)七巧板是我们祖先的一项卓越创造,用它可以拼出多种图形.请你用七巧板中标记为①,②,③的三块板(如图3)经过平移、旋转拼成图形.

(1)拼成矩形,在图4中画出示意图;

(2)拼成等腰直角三角形,在图5中画出示意图.

注意：相邻两块板之间无空隙,无重叠;示意图的顶点画在小方格顶点上.

图3

图4

图5

3 法国的“小九九”,浪漫情长

法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.下面两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国“小九九”计算7×9,左右手依次伸出手指的个数是2,4.

图6

图7

这样一种计算方法,对法国人的基本计算能力形成有着重要的促进作用;同时,作为一种文化现象,引起命题专家们的兴趣.用这样的素材作试题,增强了试卷的趣味性,体现了试卷中文化内涵的多元性.

若F′表示某种成本,则参与者1的目标是使F′最小化,而参与者2的目标是使F′最大化,据此可写出二人零和博弈模型为

而这种借助手势计算有理数的乘法,能够考查考生的信息获取能力,多项式的乘法,能够考查考生的基本运算能力、思维能力以及动手能力,有助于促进同学们生动、活泼、主动的学习.

例4 (2011年滨州)在快速计算法中,法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计算8×9时,左手伸出3根手指,右手伸出4根手指,两只手伸出手指数的和为7,未伸出手指数的积为2,则8 ×9=10 ×7+2=72.那么在计算6×7时,左右手伸出的手指根数应该分别为

A.1,2 B.1,3 C.4,2 D.4,3

本题需要学生能够根据提示语,探究并发现规律,然后作简单的运算.事实上,左、右两手未伸出的手指数与这两个数的和为10,发现这一规律后,从5×6直到9×9,均可按照题目中的提示语求得结果.因为6×7=10×3+4×3=42,所以,未伸出的手指数的积为12,只能为1和2,那么两手伸出的手指数和为3,分别为5-1=4和5-2=3.

这种阅读式探究题,读懂题目的信息很关键,正确理解题意才能分别列出伸出和未伸出的手指数.学生先耐心阅读,认真审题,把问题中所隐含的隐性条件挖掘出来,最终掌握所讲知识,再利用其解决问题.题目中蕴含着变化中有不变,不变中又有变化的辩证统一关系.

4 “杨辉三角”,图算的典范

杨辉三角形,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列.中国古代数学家在数学的许多重要领域中处于遥遥领先的地位,而杨辉三角的发现就是十分精彩的一页.

例5 (2011年凉山州)我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则：两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.

图8

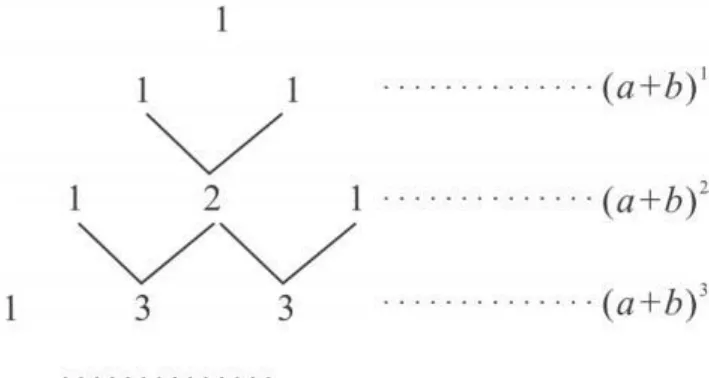
图9

(1)根据上面的规律,写出(a+b)5的展开式;

(2)利用上面的规律计算：25-5×24+10×23-10×22+5 ×2-1.

杨辉三角形与二项式定理是一对天然的数形趣遇,它把数形结合带进了计算数学.求二项式展开式系数的问题,实际上是一种组合数的计算问题.用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”.“式算”与“图算”趣遇,各扬所长,各补所短.杨辉三角形本来就是二项式展开式的算图.对杨辉三角形熟悉的考生,比如他熟悉到了它的第6行：那么他可以心算不动笔,算式到算图,一望而答.

杨辉三角形作为中考的试题,这正是义务教育课程标准中强调的“多想少算”、“逻辑思维与直觉思维并重”的结果.这类考题都与二项式展开式的系数相关,说明数形结合思想正在中考命题中进行深层次的渗透.

5 地方特色文化,在互动中升华

在中国五千年的灿烂文化中,祖先给我们留下众多的宝贵遗产,体现了中华民族各族儿女对美好生活的向往和追求,其中留存至今的各种建筑物等,仍然和我们生活在一起,成为我们的生活中不可缺少的组成部分.既是宝贵的物质财富,更是难得的精神财富,深深地扎根于当地人们的心中,成为当地人们的精神支柱,成为当地人们的精神文化的象征.弘扬她们、保护她们,成为当地人们义不容辞的责任.各地的命题专家拿她们来“说事”,也是再自然不过了.

例6 (2011年扬州)古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工作队每天整治12米,B工程队每天整治8米,共用时20天.

(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下：

根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组：

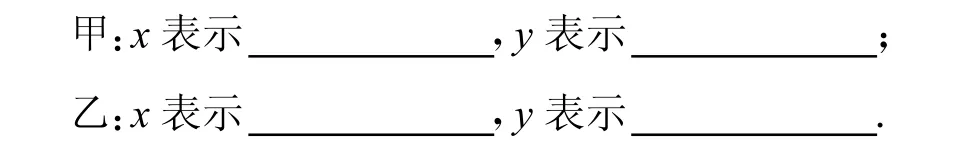
(2)求A,B两工程队分别整治河道多少米.(写出完整的解答过程)

例7 (2011年永州)永州市新田县的龙家大院至今已有930多年历史,因该村拥有保存完好的“三堂九井二十四巷四十八栋”明清建筑,而申报为中国历史文化名村.如图是龙家大院的一个窗花图案,它具有很好的对称美,这个图案是由：①正六边形;②正三角形;③等腰梯形;④直角梯形等几何图形构成,在这四种几何图形中既是轴对称图形又是中心对称图形的是_______(只填序号).

图10

6 回文句,中华文化的奇葩

例8 (2011年岳阳)下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是

A.上海自来水来自海上

B.有志者事竟成

C.清水池里池水清

D.蜜蜂酿蜂蜜

在本题中,“上海自来水来自海上”等三句,是用“回文”体现数学中的对称,用文学的趣味增强数学的趣味,用文学美衬托数学美.

回文,也写作“回纹 ”、“回环”.它是汉语特有的一种使用词序回环往复的修辞方法和艺术表现形式,是中国古代独特的文化现象,具有典型的对称美,文体上称之为“回文体”.回文,充分展示并利用了汉语以单音节语素为主和以语序为重要语法手段这两大特点,有形式变化的美丽,读来回环往复,绵延无尽,妙趣横生,不仅颇具欣赏价值,以颇有意兴盎然的情趣与美感.回文,不失为中华文化独有的一朵奇葩.回文,虽为文字游戏,诚然意境悠远,出神入化,令人发美不胜收之叹,也陶冶了学生的情操.

总之,通过学习、思考这些清新扑面、趣味盎然中考试题,感受到不仅仅是在解答中考试题,更像是参加一次文化盛宴,享受着文化的熏陶,接受着五千年文化的洗礼.通过解答这些中考试题,也在吸收着文化,提升自我的文化底蕴.

20110722)