对一道中考试题的解法探究
2011-08-25277223山东省枣庄市第十一中学张建响
277223 山东省枣庄市第十一中学 张建响
277200 山东省枣庄市第十八中学 李耀文
对一道中考试题的解法探究
277223 山东省枣庄市第十一中学 张建响
277200 山东省枣庄市第十八中学 李耀文
对中考试题的探究是教师们在教学和复习中常做的一件有益事情.本文以2011年一道中考试题进行探究,供读者们赏析参考.
1 试题呈现
江苏省连云港市2011年高中段学校招生统一文化考试数学试题第28题:
(1)有一条边对应相等的两个三角形的面积之比等于这条边上的对应高之比;
(2)有一个角对应相等的两个三角形的面积之比等于夹这个角的两边乘积之比;
……
现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)

问题2 若有另一块三角形纸板,可将其与问题1中的△ABC拼合成四边形ABCD,如图2,Q1,Q2三等分边 DC.请探究 S四边形P1Q1Q2P2与S四边形ABCD之间的数量关系.
检视父母教养范式的适切性,就是检视其合理性和有效性。“鞋子合不合脚,脚知道”。与孩子的个性和成长需求契合的家庭教育,对孩子成长产生积极的正向影响,反之亦然。检视家庭教育范式的适切性,要检视家长的家庭教育动机、教育目标,检视日常生活中亲子双方的情绪体验和行为反应等。如果消极的劣性的情感体验多,就要对家庭教育多加注意,及早发现问题和解决问题。

图1

图2
问题3 如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边 DC.若 S四边形ABCD=1,求 S四边形P2Q2Q3P3.
问题4 如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.请直接写出含有 S1,S2,S3,S4的一个等式.

图3

图4
点评 该试题是以“有一条边对应相等的两个三角形的面积之比等于这条边上的对应高之比;有一个角对应相等的两个三角形的面积之比等于夹这个角的两边乘积之比”为知识的生长点,考查了学生的基础知识、基本技能和基本方法,以及知识的迁移能力和灵活运用知识的能力.从问题的设计到解决方式上,呈现出知识的多样性、灵活性和拓展空间,较好地考查了学生的数学思维能力和综合运用知识分析问题、解决问题、提出问题的能力.本题的确是一道层次分明,梯度合理,具有很好区分度的中考试题.
2 试题答案回放
下面给出命题者提供的参考答案.
问题1



图5
所以

由P1,P2三等分边AB,R1,R2三等分边AC,Q1,Q2三等分边DC,

点评 由上述参考答案可以看出命题者的意图.充分体现出该试题所考查的是学生解决探究数学问题的重要思想方法——化归(即“化未知为已知”)和类比思想.
3 试题解法再探
学习数学,离不开解题.从不同的角度,用不同的方法,去探索解答同一道数学问题的途径,开展一题多解活动,是提高解题能力、培养创新精神的有效方法.它有利于牢固掌握数学的基础知识和基本技能,有利于提高分析问题和解决问题的能力,有利于发展思维的灵活性和创造性.下面给出本试题参考答案以外的多种解法,供读者们鉴赏.
问题1 (略)
问题2
别证1 如图6,连接AQ1,P1Q2,P2C,再设 h1,h2,h3分别是A,P1,P2到CD的距离.由P1,P2三等分边AB,可知2h2=h1+h3.
又DQ1=Q1Q2=Q2C,则有

图6


别证2 如图7,设P,Q分别是AB,CD的中点,连接PD,PQ1,PQ2,PC,易证知

图7

别证 3 如图 8,连接AQ1,P2Q1,P2C,由于 P1,P2三等分边 AB,Q1,Q2三等分边DC,则易知有

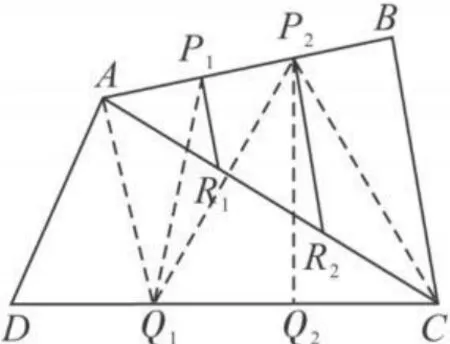
图8


别证4 如图9,取四边形ABCD的四边AB,BC,CD,DA的中点 P,N,Q,M,并设PQ与MN的交点为O,且所成的角为 α.则有:
易证知O是PQ和MN的中点,MN平分P1Q1和P2Q2,
且有MR=RT=TN.由四边形面积公式有:


图9
别证 5 如图 10,设BA,CD的延长线相交于O点,且记AB=3a,CD=3b,OA=c,OD=d,∠BOC=α,则有


图10

点评 此法是借助面积计算的方法,无需特殊的技巧和繁杂的运算,确实为一种简便易行的方法,但运算中应用到“三角形的面积等于三角形任意两边与其夹角正弦积的一半”.
问题3的别解
如图11,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC,P1Q1,P2Q2,P3Q3,P4Q4将四边形ABCD分成五个部分,面积分别为S1,S2,x,
S3,S4.由问题2的结论,易知有2x=S2+S3,


图11
问题4的别解
如图12,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3将四边形ABCD分成四个部分,面积分别为S1,S2,S3,S4.由问题2的结论,易知有:2S2=S1+S3
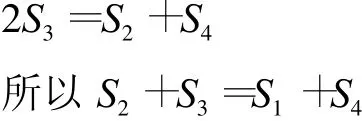
点评 通过上面我们清楚地看出,问题3,4的别解,其实是对问题2结论的直接运用.这可能是命题者设计的初衷(其中问题4只要求直接写出含有S1,S2,S3,S4的一个等式,不作理由阐述,可能是为了降低试题难度).

图12
20110810)
