杨辉三角形模5的绝对最小余数分布的分形结构特征

朱桂静， 吴 康

(华南师范大学 数学科学学院，广东 广州 510632)

杨辉三角形模5的绝对最小余数分布的分形结构特征

朱桂静， 吴 康

(华南师范大学 数学科学学院，广东 广州 510632)

定义杨辉三角形中一些特殊的三角形：n度基三角、n度零三角、n度倍三角、n度反三角、n度叁倍三角、n度三角，并在此基础上猜想和证明了杨辉三角形中n+1度基三角可由n度三角通过某种特定的排列得到，从而论证了杨辉三角形中组合数模5的绝对最小余数分布具有自相似结构特征.

杨辉三角形；自相似结构；模5

0 引言

目前对于杨辉三角形中组合数整除性的研究十分丰富,如杨辉三角形被素数整除的组合数及个数等.然而针对杨辉三角形模5分布的结构特征的研究较少,而在将杨辉三角形中的每个组合数换做模5的绝对最小余数后，其分布图似乎与谢尔宾斯基三角具有某种相似性[1].是否杨辉三角形模5的分布结构具有某种特殊结构呢？

1 引理[2]

引理1设p是质数，m为正整数，n为非负整数.m,n的p进制表示为

m=(asas-1…a1a0)p，n=(bsbs-1…b1b0)p，

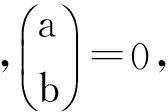
2 杨辉三角形中的相关新定义

图1 2度基三角Fig.1Two dimension based triangles

图2 2度零三角Fig.2 Tow dimension zero triangle

定义6n度三角:将所有的n度基三角、n度零三角、n度反三角、n度倍三角、n度叁三角统称为n度三角.

3 杨辉三角形模5分布的分形结构猜想

由定义可知，n+1度基三角有5n行，即有5个5n-1行.不妨将n+1度基三角平分为5层，称其第i·5n-1行到第(i+1)·5n-1-1行为n+1度基三角的第i层，其中0≤i≤4.如i=1时，第5n-1行到第2·5n-1-1行为n+1度基三角的第1层.

下面猜想，n+1度基三角可由n度三角通过以下方式组合得到：

1)n+1度基三角第0层是一个n度基三角；

2)n+1度基三角第1层是n度基三角+n度零三角+n度基三角顶行对齐的排列.

3)n+1度基三角第2层是n度基三角+n度零三角+n度倍三角+n度零三角+n度基三角顶行对齐的排列；

4)n+1度基三角第3层是n度基三角+n度零三角+n度叁三角+n度零三角+n度叁三角+n度零三角+n度基三角顶行对齐的排列；

5)n+1度基三角第4层是n度基三角+n度零三角+n度反三角+n度零三角+n度基三角+n度零三角+n度反三角+n度零三角+n度基三角顶行对齐的排列.

例如当n=1时，3度基三角第0层和第1层如图3所示.若用一个△或▽表示一个n度三角,则n+1度基三角可表示成图4所示的形式. 由此猜想：杨辉三角形模5分布具有自相似结构(分形中的一种常见结构).

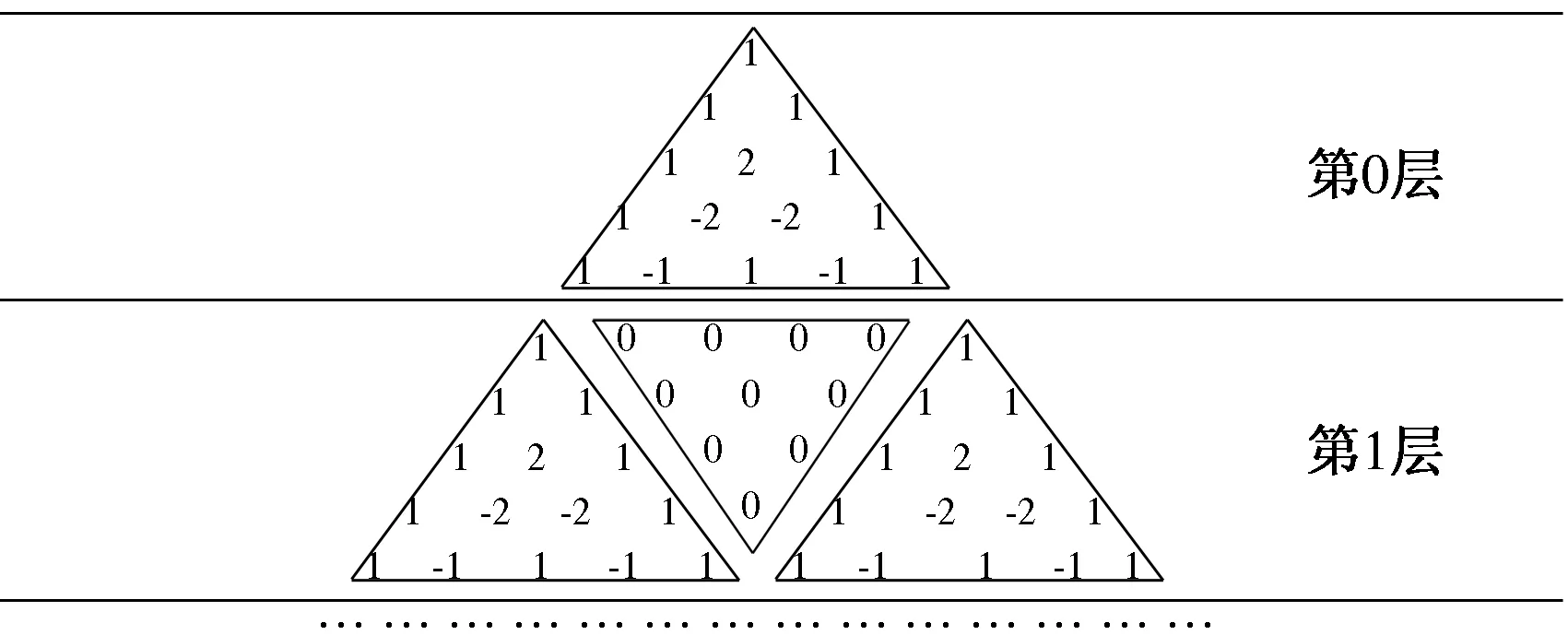
图3 3度基三角(部分)Fig.3 Three dimension based triangles(part)

图4 由n度三角构成的n+1度基三角Fig.4 The triangle formed by 3 dimension based triangles

4 杨辉三角形模5分布的自相似结构证明

定理1在n+1度基三角中，第i层第j行第k+1项恒有

(1)

故命题得证[3-5].

推论1在n+1度基三角中，第i层第j行第j+i·5n-1-k+1项恒有

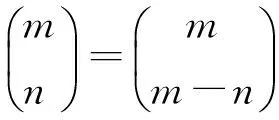
定理2在n+1度基三角中，第4层第j行第k+2·5n-1+1项恒有

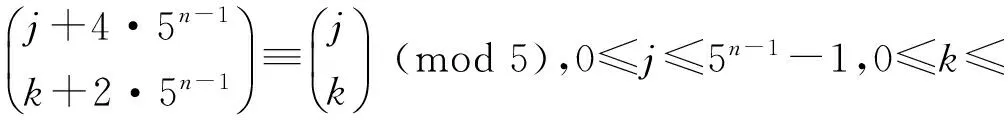
由引理1可得

所以命题得证.

定理3在n+1度基三角中，第i层第j行第k+1项恒有

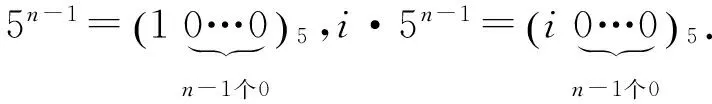
由引理1可得

所以命题得证.

推论2在n+1度基三角中，第i层第j行第j+i·5n-1-k+1项恒有

同理可得

定理4在n+1度基三角中，第i层第j行第k+1项恒有

定理5在n+1度基三角中，第2层第j行第k+5n-1+1项恒有

定理6在n+1度基三角中，第4层第j行第k+5n-1+1项恒有

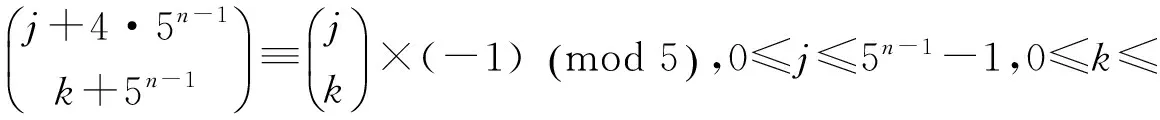
推论3在n+1度基三角中，第4层第j行第j+3·5n-1-k+1项恒有

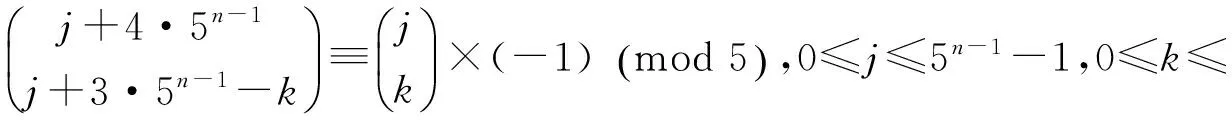
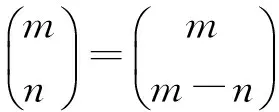
定理7在n+1度基三角中，第3层第j行第k+5n-1+1项恒有

5 结束语

从分形数学的角度研究杨辉三角形中模5分布的结构特征，从看似杂乱无章的分布中揭示出其隐藏的规律性、层次性，可以通过杨辉三角形模5分布的局部认识整体.再者，杨辉三角形模5的自相似结构，可以类比推广到杨辉三角形模p的余数分布结构中，其中p为任意素数.

[1] 陈颙，陈凌．分形几何学[M]．北京：地震出版社，2005:163-180．

[3] 胡圣团.关于组合数的几个整除问题[J].中等数学,2010(5):7-10.

[4] 胡恩良,朱维宗.杨辉三角形中的几条组合性质[J].云南民族学院学报:自然科学版,2002,11(3):132-135.

[5] 曹汝成.组合数学[M].广州：华南理工大学出版社,2001.

The Self-similar Structure of the Distribution of Absolute Minimum Remainder of Combinatorial Number Mod Five of Pascal Triangle

ZHU Gui-jing, WU Kang

(SchoolofMathematicsSciences,SouthChinaNormalUniversity,Guangzhou510632,China)

Some specific triangles in Pascal Triangles are defined, namelyndimension based triangle,ndimension zero triangle,ndimension double triangle,ndimension contrary triangle,ndimension contrary-double triangle andndimension triangle. Based on these definitions, a hypothesis is put forward. It proves thatn+1 dimension based triangle in Pascal Triangle can be achieved through some particular arrangement ofndimension triangle. Thus, the distribution of absolute minimum remainder of combinatorial number mod five shows a self-similar structure.

Pascal Triangle; self-similar structure; mod five

2014-11-04

朱桂静(1990—)，女，广东梅州人，华南师范大学数学科学学院在读硕士研究生.

10.3969/j.issn.1007-0834.2015.01.007

O1

1007-0834(2015)01-0021-04