巧用特例法解选择题
2011-08-25225700江苏省兴化市第一中学
225700 江苏省兴化市第一中学 杭 静
225700 江苏省兴化市教育局教研室 陈德前
巧用特例法解选择题
225700 江苏省兴化市第一中学 杭 静
225700 江苏省兴化市教育局教研室 陈德前
选择题的特点是小而灵活、知识覆盖面广、考查面宽、求解方法灵活、答案明确、评分客观,同时也便于阅卷,因而测试的信度高,操作方便.在各地的中考试卷中,每份试卷都有选择题,掌握选择题的解题方法与技巧是提高中考成绩的关键因素之一.根据“只有一个选择支是正确的”这一重要信息,在含有一般元素的选择题中,结合选择支的特点,利用符合条件的特例,代入题干和选择支中,分别进行分析、思考、计算、推理,其中数值相等或符合条件者即为选择的答案,这就是特例法,它是解答选择题的一个常用方法与技巧.下面举例说明如何运用特例法解选择题,供研讨.
1 取特殊值
例1 若m+n=3,则2m2+4mn+2n2-6的值为
A.12 B.6 C.3 D.0
解析 解决本题的一般方法是将已知条件转化为m=3-n(或n=3-m)代入或将求值式转化为2(m+n)2-6再整体代入.但如果注意到题目的已知条件m+n=3,可以巧用取特殊值的方法来简捷求解:取m=0,则n=3,原式 =0+0+18-6=12,选A,口算即可得到答案.

解析 本题的一般解法是去分母,转化为整式方程后求出x,再由x为正数得到不等式,进而求出a的取值范围,再结合分式方程的增根的概念就可以得到答案.但注意到选择支的特征,可借助于取特殊值的方法来简便处理:取a=1,代入原方程,可知解为负数,不符合要求,所以排除A,B;再将a=-2代入,此时方程无解,所以C也要排除,所以选D.
A.和为60° B.和为45°
C.互为补角 D.互为余角
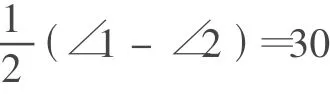
2 取特殊点
例4 如图1,把图1中的⊙A经过平移得到⊙O(如图2),如果图1中⊙A上一点P的坐标为(m,n),那么平移后在图2中的对应点P′的坐标为
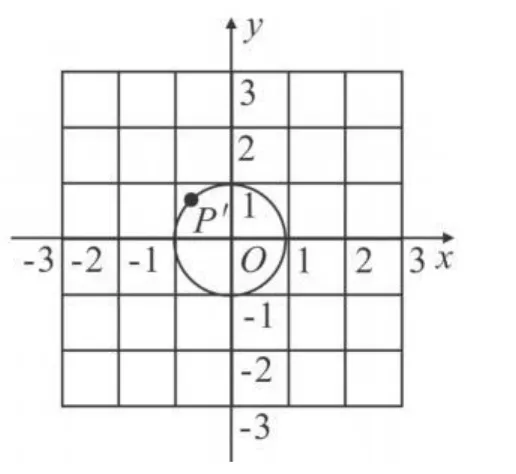
图2
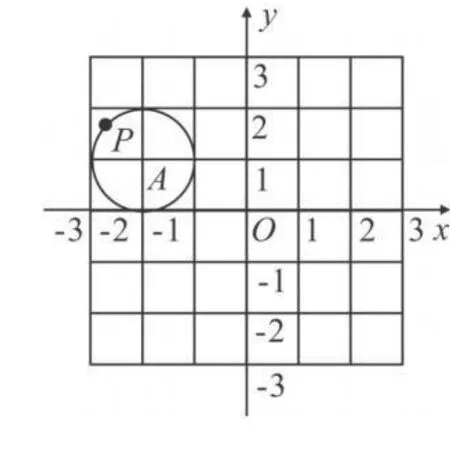
图1
A.(m+2,n+1) B.(m-2,n-1)
C.(m-2,n+1) D.(m+2,n-1)
解析 仅从点P到点P′的变化是难以得到结论的,考虑特殊的点——圆心的变化,就可以发现,圆心A的坐标为((-2,1),经过平移后到点O,其圆心为(0,0),即将点A先向右平移了2个单位,再向下平移了1个单位(或先向下平移了1个单位,再向右平移了2个单位),因此,点P(m,n)到点P′也是先向右平移了2个单位,再向下平移了1个单位(或先向下平移了1个单位,再向右平移了2个单位),所以点P′的坐标为(m+2,n-1),选 D.
例5 (天津市中考题)在平面直角坐标系中,先将抛物线y=x2+x-2关于x轴作轴对称变换,再将所得的抛物线关于y轴作轴对称变换,那么经两次变换后所得的新抛物线的解析式为

解析 在y=x2+x-2的图象上取一个特殊点(2,4),它关于x轴的对称点为(2,-4),所得的点(2,-4)关于y轴的对称点为(-2,-4),将点(-2,-4)代入各个选择支,只有选择支C符合,所以应选C.
例6 如图2,⊙O是正方形ABCD的外接圆,点P在⊙O上,则∠APB等于
A.30° B.45° C.55°
D.60°
解析 取点P为特殊点C(或点 D),易知∠APB=∠ACB=45°,选B.
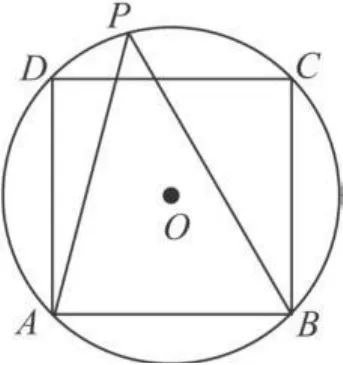
图2


图3


3 取特殊图形
例8 (甘肃省庆阳中考题)如图4,在宽为20米,长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为
A.1 米 B.1.5 米 C.2 米 D.2.5 米
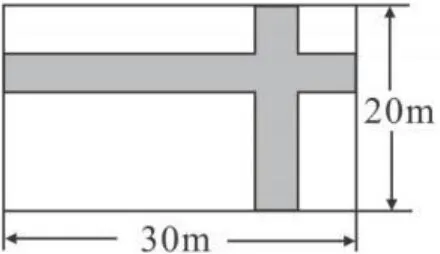
图4
解析 本题的一般解法是设修建的路宽应为x米,从矩形总面积中减去两条道路的面积,得到方程:30×20-[30x+(20-x)x]=551,得x=1,选A.有些考生重复减去交叉部分的面积,得到30×20-30x-20x=551的错误方程.为了减少这种错误,可以考虑特殊图形——利用平移的方法将它转化为规则图形来思考:由题意转化为图5,设道路宽为x米,根据题意,可列出方程为,(30-x)(20-x)=551,整理得x2-50x+49=0,解得x1=49(舍去),x2=1.所以道路宽为1米,选A.

图5
例9 (江苏省扬州市中考题)AD为△ABC中BC边上的中线,则AD与(AB+AC)的关系是
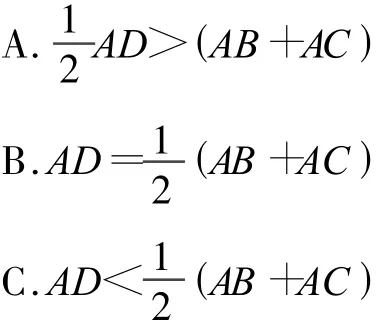
D.不能确定大小

例10 (四川省绵阳市中考题)如图6,在正方形ABCD的外侧,作等边△ADE,BE,CE分别交AD于G,H,设△CDH,△GHE的面积分别为S1,S2,则
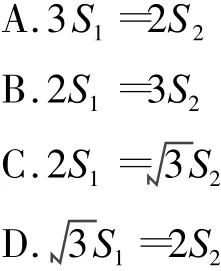

图6
在用特例法解题时,要注意以下三点:①取特殊值尽可能简单,有利于计算;②各选择支均应检验;③若在某特殊值情况下有两个或两个以上的选择支与题目结论相符,则应另选一特殊值再检验,若选择支无交叉关系,则可一次到位.
20111012)
