基于极化变换的极化匹配滤波器及其通带理论

刘 涛 胡生亮 陈 旗 黄高明 高 俊

(海军工程大学电子工程学院,湖北武汉430033)

1.引 言

极化滤波的关键在于利用目标信号和干扰噪声信号在极化特征上的差异,在数学上可以建模为带有约束的线性或者非线性最优化问题。在现在雷达极化滤波中一般所提的滤波概念为以信干噪比(SINR)最大化准则的极化滤波器,传统上基于SINR准则的滤波器可以看作是匹配滤波器,可以称SINR最大化为准则的极化滤波器为极化匹配滤波器[1]。

延承电磁波传播与接收的研究思路,对完全极化信号,Guili,Boerner等研究了最优极化叉,即共极化零点,交叉极化零点和交叉极化最大点形成了一个极化叉,极化叉所在的平面处于poincaré球面上某个大圆上;对于部分极化信号,Van Zyl借助laglange乘子法获取了其最优解,但是,需要求解六次方程的根,计算比较复杂;Czyz提出利用相干法和非相干法两种方法来消除部分极化杂波;在同时存在部分极化信号和干扰时,Poelman研究了多凹口逻辑极化对消器(MLP)。Gherardelli提出了多凹口自适应极化对消器(MLP-SAPC),并与单凹口极化对消器和MLP进行了比较;当同时存在完全极化的信号和干扰,以及白噪声时,Stapor定义了信干噪比(SINR)等式,并提出了几种最优化策略,指出SINR的最优极化点位于一个圆上[1]。王雪松等推导了局部最优接收极化解,杨运甫等提出了基于极化椭圆参数的三步搜索比较法的数值求解方法[2]。当同时存在噪声、部分极化的信号和干扰时,王雪松等利用Lagrange乘子法求取了SINR最优化的两个备选解,同时提出了SINR极化滤波器通带的概念[3-4]。徐振海等利用矢量梯度方法求取了SINR等式的解析解[5]。王雪松等以SINR极化滤波器为参照标准,提出了极化滤波器的优选方案和判别条件[6]。作者对部分极化电磁波统计特性的研究也为极化滤波器的设计提供了指导[7]。但是目前极化滤波处理存在的问题主要是:一滤波原理与算法只能针对二维数据,不能处理高维极化散射的数据处理,没有给出极化白化滤波与匹配滤波的衔接;二极化通带表征复杂,需要在三维球面上表征,简化通带的表达将是极化滤波处理的理论的一个实际需求。

2.极化匹配滤波器的Jones矢量解

在经典的Stokes矢量的表征理论中,干扰和噪声是分开计算的,并且将白噪声的极化假设为未极化波。实际上,噪声随着环境和接收机内部扰动的变化,都会呈现出一定的极化状态,可见白噪声的极化实际上也未必是未极化波[4]。因此,可以将干扰和噪声叠加起来,构造新的基于总体干扰信号的极化表达式。在干扰和噪声不相关的情况下,通过干扰信号和噪声信号的Stokes矢量叠加就能得到总体干扰极化形式。

假设雷达接收到的电磁波的复矢量表示为Jones矢量形式[8],即

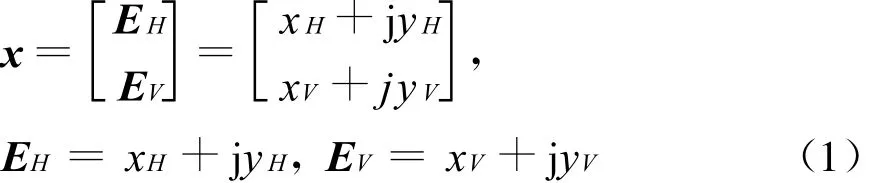
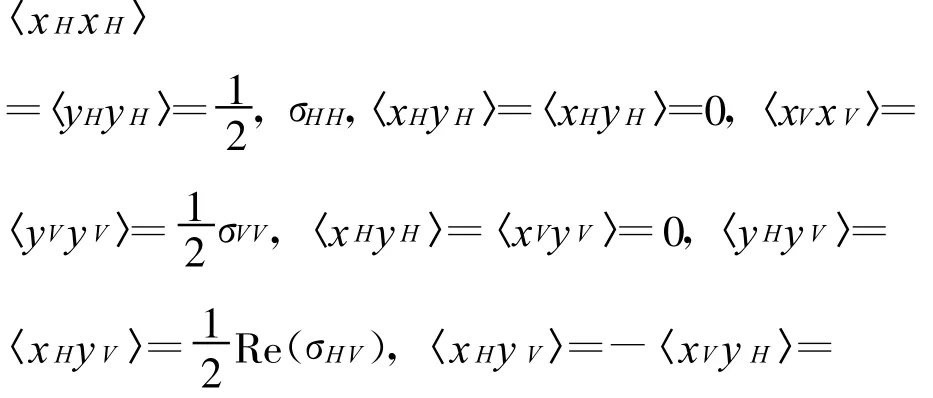
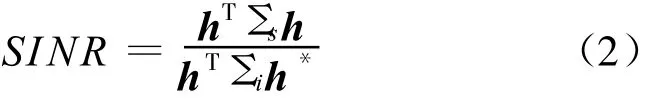
显然,寻求信噪比最大化的最优接收极化与相干矩阵的绝对强度是没有关系的,最优接收极化一般划归为矩阵的特征值问题.

式中,h是最大特征值λ所对应的特征向量。根据部分极化相干矩阵的正定性上式变换为

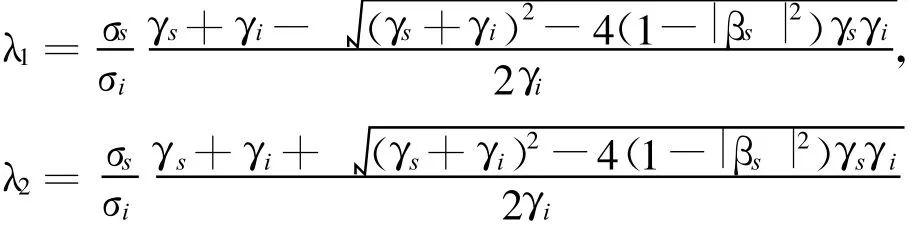
可见最大的特征值为

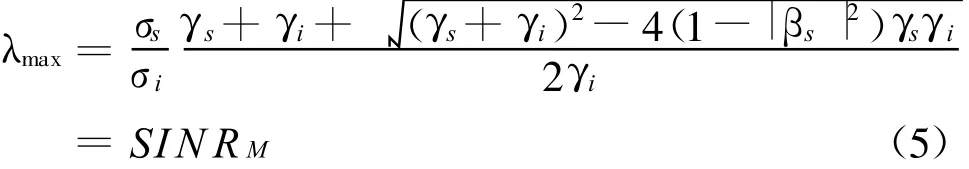
最大特征值对应的特征矢量为

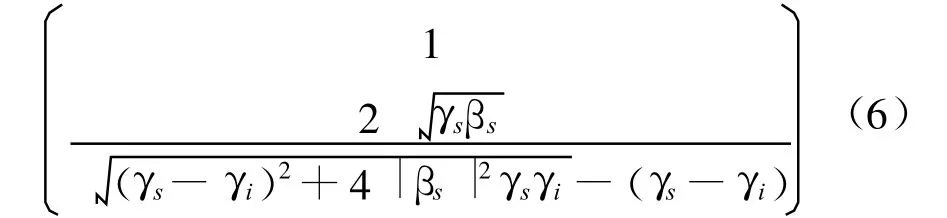
附录A证明了通过Stokes参数计算的与通过极化复平面计算的最优极化的一致性。同时可以得到,最优极化与特征极化基下信号相干矩阵相位是相同的。

由式(6)得到

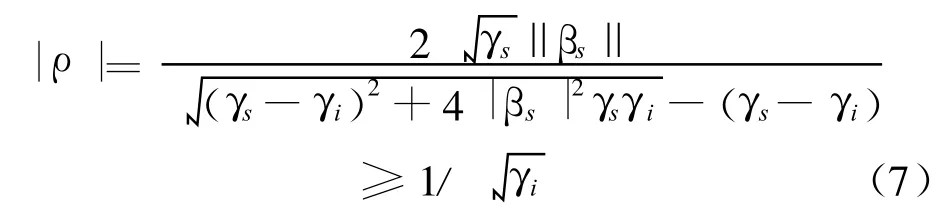
可见如果干扰噪声相干矩阵对角化后γi≤1,那么,在极化复平面上极化匹配滤波器的最优极化必定在单位圆上或者圆外。

另外,值得说明的是在二维的电磁波极化特性上利用了极化基变换的方法简化了最优极化的求解,得到了与已有结论完全一致的结果,验证了方法的正确性。同时,在极化合成孔径雷达(SAR)图像处理中,给出的往往是3×3或者4×4甚至也有更高维数据处理的需求[10-11],这是传统的Stokes矢量分析方法难以解决的,同时现有文献针对的极化SAR数据处理给出的都是假设3×3矩阵交叉元素为0的特殊情况[12],对于一般情况的分析由于其复杂性没有给出理论分析与结果。这里提出的相干矩阵酉对角化思想可以完全适用于高维极化匹配情况,这为在实际中高维极化匹配滤波的应用提供了简单可靠的技术途径。其过程就是首先将高维噪声相干矩阵酉对角化(对应极化基变换),然后根据最大信噪比的Jones矢量表达形式求取最优极化,最后通过相应的逆变换就可以得到原极化基下的表达方式。

3.极化白化-匹配联合滤波器

极化白化滤波器的提出是基于线性滤波器噪声起伏性最小的原则[12],在数学上极化白化滤波器的线性变换等价于特征值分解理论中的迷向圆变换[8,13]。根据极化白化滤波器的定义,将经典的三维模型降为两维,极化白化滤波器的接收天线为全极化天线,那么根据噪声的相干矩阵 ∑i=,那么相干矩阵的酉矩阵对角化为:∑i=UHA i U,易得极化匹配滤波器的线性变换矩阵为A-1/2i U,这样本质上干扰噪声就变成了完全未极化波,在这里考虑已经通过极化基变换对角化。此时信号相干矩阵变为干扰噪声相干矩阵记为,那么 线性变换公式为

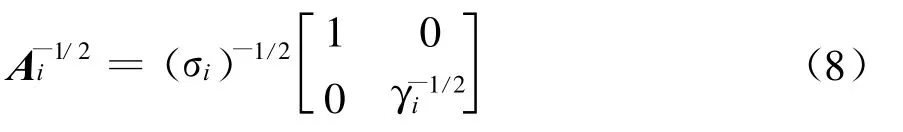
那么极化白化滤波器的全极化输出信噪比为

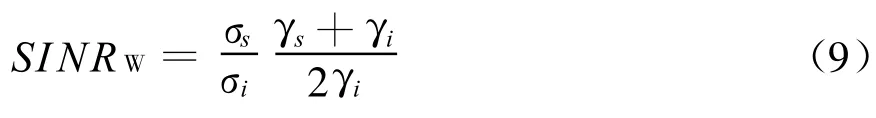
可见,经过极化白化处理后,滤波后全极化信噪比未必比原来的全极化信噪比更大。在极化SAR数据处理中极化白化滤波器到此取模后并未接着对信号进行继续增强[12]。为了让信噪比能够达到最优,在信号极化状态已知的前提下,可以在极化白化滤波器后串联一个极化匹配滤波器,为了区别已有的极化白化滤波器称之为极化白化-匹配滤波器。那么利用式(5),容易得到通过联合滤波器的输出信噪比为

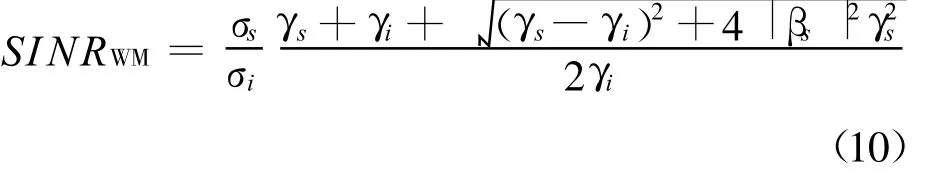
利用附录B相同的方法,可以得到极化白化-匹配联合滤波器的输出信噪比不低于全极化信噪比的结论。那么极化匹配滤波器与极化白化-匹配滤波器相比,哪个滤波器能够获得更大的信噪比呢?首先对两种信噪比表达式进行变形,得到两种信噪比的表达式变换为

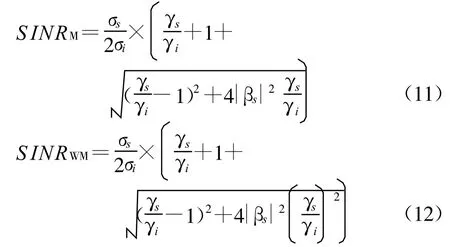
易知 γs≥γi时,SINRWM≥SINRM;γs＜γi时,.那么两种信噪比随的变化规律如图1所示(不妨假设共有系数=2)。依据极化滤波器的选择与判决原则[6],以上分析为实际应用中极化滤波器的构建和选择提供了理论依据。

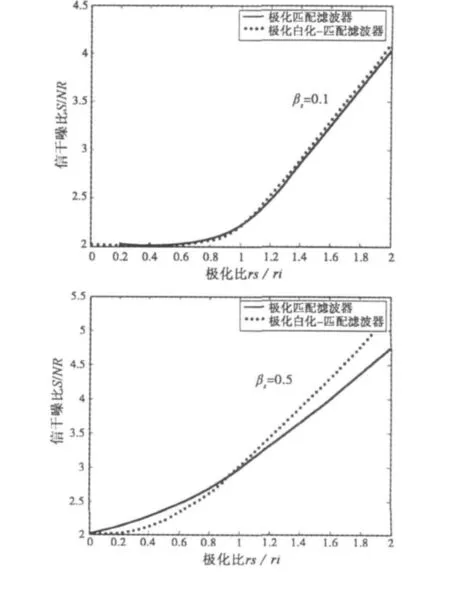
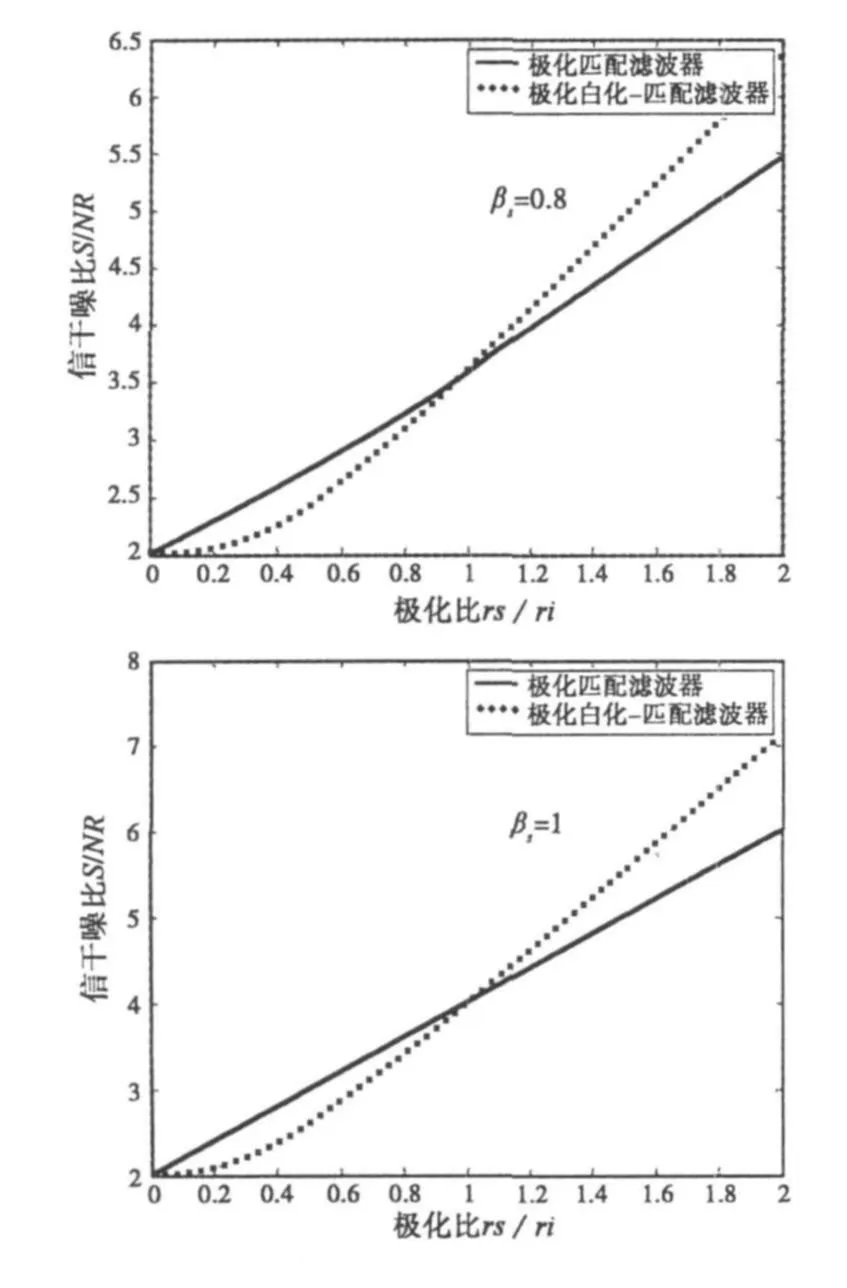
图1 极化匹配滤波器与极化白化-匹配滤波器的性能比较

4.极化复平面上的极化通带理论

Poincaré球上所定义的极化通带是一个极化球冠,对电磁波极化滤波的表征和分析是十分有用的工具。但是由于它是一个三维球面,所以有时很难将球面上各点对应的极化状态进行可视化处理,特别是利用计算机绘图技术进行表征与分析时,总体上来讲通过计算机绘出的Poincaré球上的三维极化状态点集远不如一张平面图看起来直观和易于理解[13]。因此,利用第3节得到的极化复平面上的最优极化方法来求解极化复平面上极化通带的具体表征形式。但是到底极化通带在极化复平面上表现为何种形式呢?理想的情形当然是圆,这样滤波器非常容易判决。

根据极化通带的概念,在极化复平面上可以表征为

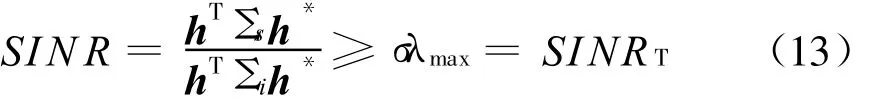
这里0≤σ≤1,根据附录C可以给出极化复平面上的极化通带一般为一个圆的内部或者外部。不妨给出一组普通的极化参数实例,信号与干扰噪声的相干矩阵为

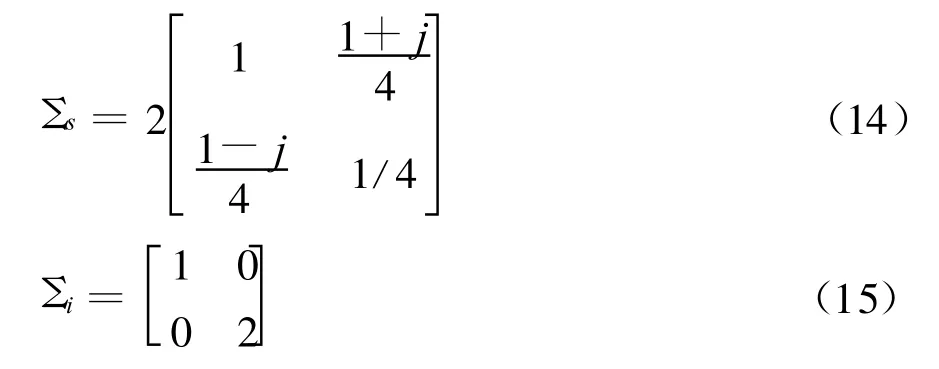
可见极化通带圆心在一条直线上,即在与信号相干矩阵相位完全相同的直线上。随着通带门限的降低,极化通带将逐渐覆盖半个极化复平面,如图2所示。

那么附录C中式(2)变为

表示通带为平面极化域上直线的上半平面区域,如图3所示。

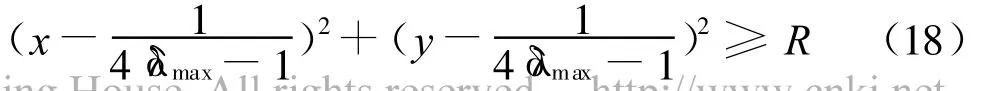
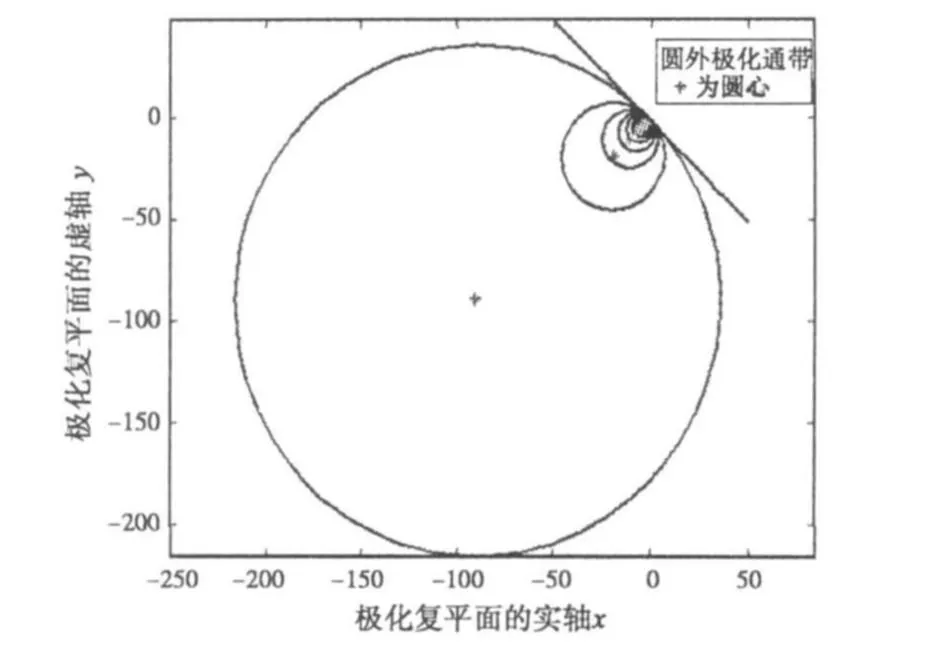
图4 圆外极化通带

可见随着所需信噪比数值的不断减少,通带在极化复平面上由圆内区域逐渐变换为某一直线之上的半平面区域,然后变化为另半平面内圆外的所有区域,最后达到最小值后成为全通状态。同时值得指出的是,最优极化点始终在通带内,但是与圆心并不重叠,这一点从极化通带圆的相切可以看出。极化通带表征模式简单直观,易于理解并对相应数据处理非常有利(可对比文献[1])。

5.结 论

主要利用相干矩阵的可酉对角化特点,借助极化基变换思想,通过矩阵特征值与特征矢量的方法求取了极化匹配滤波器的极化天线最优化接收解析解,也就是信干噪比(SINR)等式的最优极化Jones矢量解,所提的极化基变换思想可以推广到一般高维极化匹配滤波的数据处理中。然后在不同背景下分析了极化白化滤波器与匹配滤波器的性能差异,提出了可通过信号处理方法虚拟实现的极化白化-匹配联合滤波方法,对实际工程应用中极化滤波器的分析与选择具有一定指导价值。针对极化匹配滤波器,分析了其最优极化接收Jones矢量在极化复平面上的表征,同时在极化复平面上分析了极化通带的特性,得出在poincaré球上的极化球冠的通带映射到极化复平面变化为极化圆的表征模式。随着所需信噪比数值的不断减少,在极化复平面上通带由圆内区域逐渐变换为某一直线之上的上半平面区域,最后变化为下半平面圆外的区域,最后成为全通状态。在表达形式上简单直观,物理意义明确,特别适合于计算机仿真与实际计算,这些为部分极化信息的滤波处理提供了简单有效的技术手段。随着极化技术在雷达对抗中应用的不断深入[14],如何通过实验充分利用最优极化滤波特性提高雷达极化目标的检测与识别能力,将是下一步研究的重点内容。

附录A 极化复平面上的极化匹配滤波器与部分极化下SINR最优的一致性证明

利用已有Stokes矢量参数进行最优化处理结果,经过重新组织,得到物理意义明确的表达结果为[1]

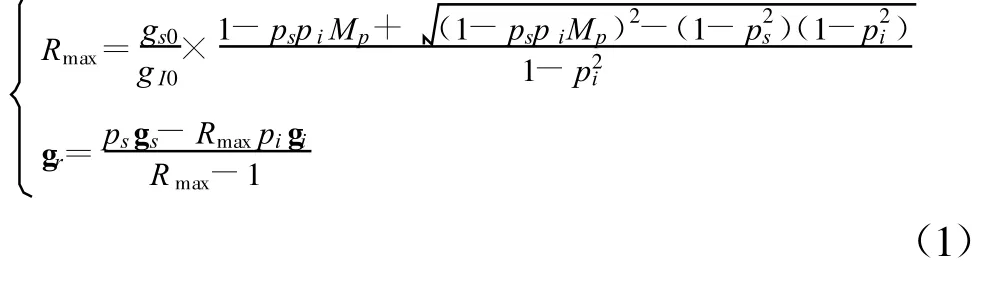
式中:R max为最大SINR;gs0为信号平均功率;g I0为干扰噪声(包含色噪声、各极化通道噪声不同的一般情况)总平均功率;g s为信号Stokes子矢量;g i为干扰(包含噪声)的信号Stokes子矢量;p s和p i分别为表示信号极化度和噪声干扰共同的极化度,定义为信号与干扰噪声整体极化匹配系数,且 ‖Mp‖ ≤1。可见,将环境噪声、接收机内部噪声和干扰信号全部整合到干扰信号中,形成统一的干扰功率和干扰Stokes子矢量,得到了形式简洁、物理意义明确的最优化结果。这个重新整理的结果比以前的结果简洁明了,影响因素也非常明确。

利用特征极化基下相干矩阵与Stokes参数的转化关系,易得

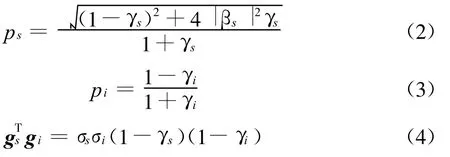
那么将式(A.2-A.4)代入式(A.1),经过简单的推导可以得到

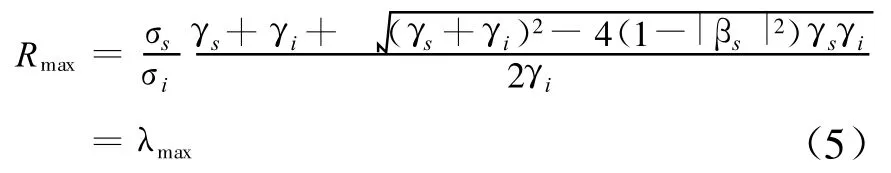
这就验证了两种解法结果的一致性,同理可以得最优极化的一致性。其实从变形出来的式(A.1)也可以看出,最优极化的值R max其实与极化基的选择或者变换是无关的,同时最优接收极化在极化基变换上满足经典Stokes子矢量的变换公式,极化基变换为极化匹配滤波器的最优化求解与简化运算提供了很好的途径。

附录B 极化匹配滤波器的输出信噪比不低于全极化信噪比的证明

由正文式(5)知

全极化信噪比一般定义为两个接收极化通道的信号能量和的比值,即

那么式(1)变形得到

下面分两种情况来讨论:

1)如果γs≥γi,那么式(3)变化为

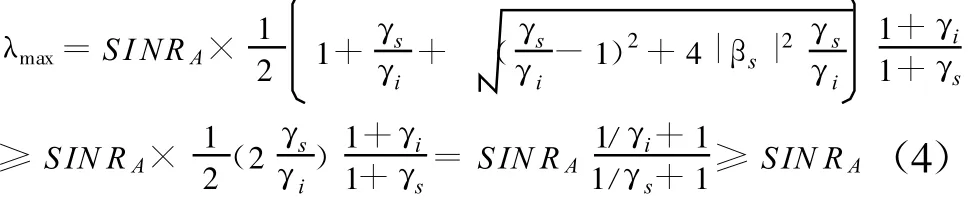
2)如果γs＜γi,那么式(4)变化为

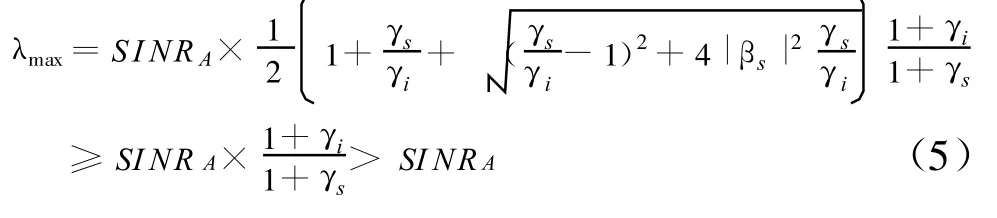
综合两种情况可见,极化匹配滤波器的接收信噪比不仅不低于任何某一极化通道的信噪比,同时还不低于全极化信噪比。

附录C 在极化复平面上极化通带约束表现为极化圆的证明

根据极化通带的概念,得极化复平面上极化通带的判决式为

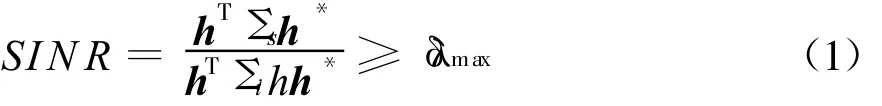
式中,0＜δ≤1,这里用直角坐标系来表征参量。不妨在干扰噪声的特征极化基下考虑极化优化问题,这样干扰噪声的极化在复平面上位于坐标原点。令接收极化中复数ρ=x+jy,信号相干矩阵互相关系数为βs=a+jb,那么式(C.1)变为

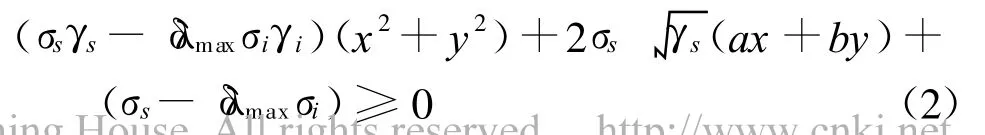
下面分三种情形进行讨论:

1)如果 Δ =σsγs-σλmaxσiγi ＜0,

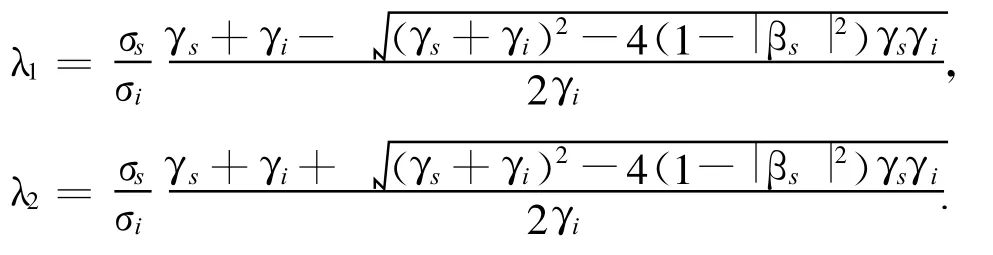
那么式(2)变为

表示通带为平面极化域上直线的上半区域。同时可以看出,如果 βs=0,那么式(4)变为 γs ≤γi,δ=γs/γi;如果此时 γs＞γi,那么,δ=1,通带就只是最优极化那么一个状态点。

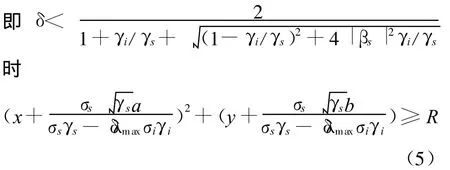
这里,

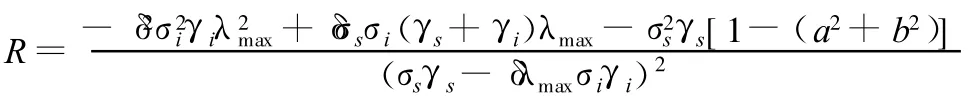
可见R为δλmax的二次曲线形式,且开口向下。它的两个根就是第二节所得到的两个非负特征值 λ1、λ2:

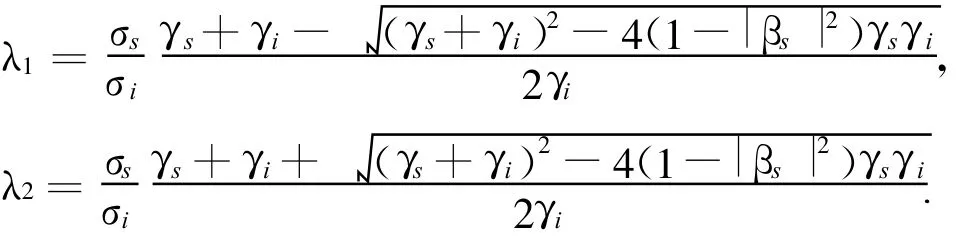
[1] 杨运甫,陶 然,王 越.部分极化情况下SINR最优极化滤波器特性分析[J].自然科学进展,2007,17(3):370-378.

YANG Yunfu,TAO Ran,WANG Yue.Optimal Polarization for SINR equation in partially polarized case[J].Progress in Natural Science(Chinese Edition),2007,17(3):370-378.(in Chinese)

[2] YANG Yunfu,TAO Ran,WANG Yue.A new SINR equation based on the polarization ellipse parameters[J].IEEE Transactions on Antennas and Propagation,2005,53(4):1571-1577.

[3] 王雪松,徐振海,代大海,等.干扰环境中部分极化信号的最佳滤波[J].电子与信息学报,2004,(4):593-597.

WANG Xuesong,XU Zhenhai,DAI Dahai,et al.Optimal filtering of partially polarized signals in theinterference background[J].Journal of Electronics and Information Technology,2004,(4):593-597.(in Chinese)

[4] WANG Xuesong,CHANG Yuliang,DAI Dahai,et al.Band characteristics of SINRpolarization filter[J],IEEE Transactions on Antennas and Propagation,2007,55(4):1148-1154.

[5] 徐振海,王雪松,施龙飞,等.信号最优极化滤波及性能分析[J].电子与信息学报,2006,(3):498-501.

XU Zhenhai,WANG Xuesong,SHI Longfei,et al.Optimal polarization filtering and its performance analysis[J].Journal of Electronics&Information Technology,2006,(3):498-501.(in Chinese)

[6] 王雪松,代大海,徐振海,等.极化滤波器的性能评估与选择[J].自然科学进展,2004,(4):442-448.

WANG Xuesong,DAI Dahai,XU Zhenhai,et al.As-sessment and choice of polarization filters[J].Progress in Natural Science(Chinese Edition),2004,(4):442-448.(in Chinese)

[7] LIU Tao,HUANG Gaoming,WANG Xuesong,et al.Statistics of the polarimetric weibull distributed electromagnetic wave[J].IEEE Transactions on Antennas and Propagation,2009,57(10):3232-3248.

[8] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[9] GOODMAN N R.Statistical analysis based on a certain complex Gaussian distribution(an introduction)[J].Annals of Mathematical Statistics 34,1963,152-177.

[10] 徐 丰,金亚秋.目标散射的去取向理论和应用(一)去取向理论[J].电波科学学报,2006.21(01):6-15.

XU Feng JIN YaQiu.Theory and application of deorientation for target scattering Part I:deorientation theory[J].Chinese Journal of Radio Science,2006.21(01):6-15.(in Chinese)

[11] 徐 丰,金亚秋.目标散射的去取向理论和应用(二)地表分类应用[J].电波科学学报,2006,21(2):153-160.

XU Feng JIN YaQiu.Theory and application of deorientation for target scattering Part II:application to terrain surface classification[J].Chinese Journal of Radio Science,2006,21(2):153-160.(in Chinese)

[12] NOVAK L M,BURL M C,IRVING W W.Optimal polarimetric processing for enhanced target detection[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(1):234-244.

[13] 庄钊文,肖顺平,王雪松.雷达极化信息处理及其应用[M].北京:国防工业出版社,1999.

[14] 丁晓松,金亚秋.海面上方运动目标和人造箔条云干扰的多普勒频移仿真[J].电波科学学报,2004,19(4):431-437.

DING Xiaosong,JIN Yaqiu.Simulation of doppler frequency shift for a moving targetand chaff cloud above theoceanic surface[J].Chinese Journal of Radio Science,2004,19(4):431-437.(in Chinese).