多径环境下海面低空目标检测技术研究

杨 勇 王雪松 张文明 肖顺平

(国防科学技术大学电子科学与工程学院,湖南 长沙 410073)

1.引 言

现代战争中飞机和导弹的低空、超低空入侵,给雷达探测提出严峻挑战,同时也给对方的地面和海面目标构成极大的威胁。对海监视雷达因受地球曲率、强烈的背景杂波(海浪、气象杂波等)和电波多径效应的影响,要在较远的距离上对掠海飞行的目标“保证发现”和“精确定位”是相当困难的。海面低飞目标的检测跟踪一直是雷达技术研究的热点问题。

雷达探测低空目标时,多径效应导致雷达波瓣分裂,从而给雷达检测、跟踪测角都带来一定影响。为了消除多径效应给雷达跟踪测角带来的严重影响,诸多学者在这方面开展了大量研究[1-4]。多径效应对雷达检测的影响相对较弱,从统计意义上讲,多径效应对雷达接收信号具有增强效果,有利于雷达对低飞目标的检测。在研究多径对雷达性能的影响效果时,首先要对多径散射进行合理建模。文献[5]较早较全面地建立了雷达多径散射模型;在总结前人研究成果的基础上,文献[6]以评估半主动雷达导引头制导性能为背景,对比分析了各种多径散射模型的优缺点,得出了不同场景下的最佳多径模型。在多径条件下雷达检测技术研究方面,文献[7]首先建立了多径散射的参数化模型,然后通过大量检测试验和分析评估,提出了具有最佳检测性能的频率分集算法。文献[8]分别针对起伏目标与非起伏目标,推导了多径环境下雷达接收信号的概率密度函数,仿真得到了特定场景下针对不同目标的最佳检测方案;文献[9]研究了天基雷达利用多径效应检测机载目标的方法,其巧妙地利用多径干扰对天基雷达接收信号的幅度调制这一现象,通过测量幅度调制频率,从而检测出目标。文献[10]综合考虑目标的多径效应以及海杂波的影响,建立了雷达目标后向散射模型,在此基础上,研究给出了不同海面粗糙度下的雷达检测性能。国内的研究主要集中在多径环境下雷达跟踪测角技术方面,在多径环境下雷达检测技术方面的研究相对较少。

以对海监视雷达探测低空飞行目标为背景,研究了多径环境下对海监视雷达采用双门限(M-N)检测器的检测性能,给出了不同环境、不同虚警概率下不同M-N检测器的检测性能曲线,对自由空间和多径环境下的雷达性能进行了对比,得到了雷达具有最佳检测性能时的最佳M值。文章第二节研究了低空环境下的目标多径散射模型,第三节推导了多径条件下雷达检测低空飞行目标的检测概率表达式,第四节结合具体场景,给出了仿真结果,总结出了各种情况下的最佳M值。

2.多径散射建模

研究多径效应对雷达检测性能影响的首要环节是对多径散射进行建模。雷达在低仰角探测海上目标时,除了海面不均匀水蒸气引起的电波折射效应外,还有海面产生的镜反射和漫散射引起的多路径干涉效应。雷达接收的回波信号是目标直接反射回来的信号与海面反射信号的叠加信号。其中,反射信号分为镜面反射信号和漫反射信号。因此,雷达接收信号可表示为

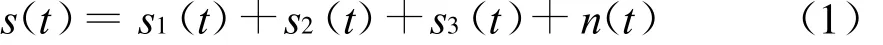
式中:s1(t)为直达波信号;s2(t)为镜面反射信号;s3(t)为漫反射信号;n(t)为噪声。

当目标高度较高时,多径效应可忽略不计,而当目标高度较低时,经海面反射的回波幅度与直达波相当,此时,须对目标信号的多径散射进行详细建模。当反射面较平坦或掠射角很小时,反射波主要以镜面反射为主,而对于粗糙表面,随着掠射角的增大,反射波的镜面反射成分逐渐减弱,漫反射成分逐渐增强。文中主要研究平静海面下雷达对掠海飞行目标的检测问题,此时,多径反射可视为理想反射,在对雷达接收信号建模时,主要考虑镜面反射回波。多径反射示意图如图1所示。

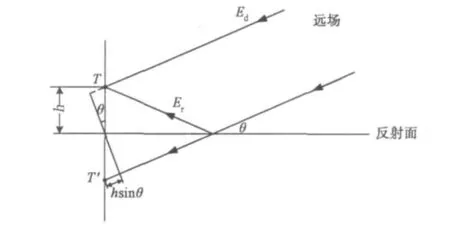
图1 多径反射几何示意图

多径散射建模的重点是对反射信号的建模,反射信号幅度主要由传播因子决定。定义传播因子v为

式中:E0为自由空间中经目标反射后雷达处的信号场强;E1为多径环境下经目标反射后雷达处的信号场强。

假定发射信号为水平极化,传播因子v可表示为[11]

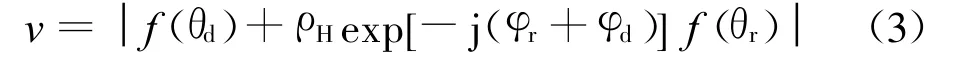
式中 :f(·)为天线方向图;θd、θr分别为直达波、镜面反射波与波束最大方向的夹角;ρH为水平极化下的反射系数;φr为反射系数的相位;φd为直达波与反射波的路程差引起的相位差。当目标仰角较低时,对于水平极化波,可以认为反射系数的幅度ρH=1,相位φr=π.直达波和反射波总的相位差可表示为

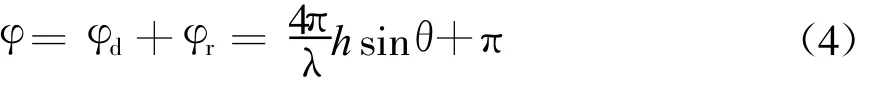
多径环境下雷达处的场强为

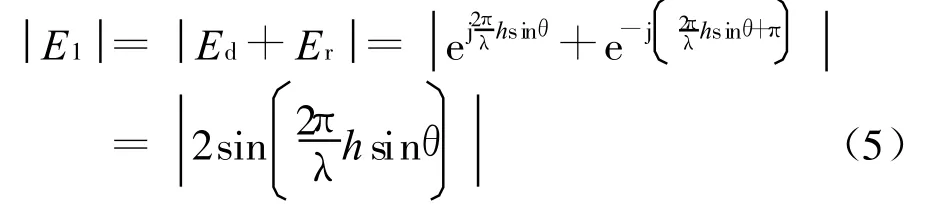
由于目标的高度和距离未知,z未知,从而传播因子未知。通常情况下,假设直达波与反射波的相位差φ服从[0,2π]均匀分布[4],即z服从[0,1/2]均匀分布。而由式(6)可以看出,z服从[0,1/2]均匀分布与z服从[0,1/4]均匀分布,对于|E1|而言是等效的。当电波传播的单程距离变化λ/4时,即z变化1/4时,接收信号的相位即发生180°翻转,在微波频段内,λ/4的取值在15～30 cm 之间,这一测量精度目前雷达是很难达到的。但在一些具体场景下,可认为z服从特定分布。例如:雷达工作中心频率为3.3 GHz,带宽为300 MHz,目标飞行高度为100 m,掠射角θ=1°,则z的取值范围为18.33～20.07此时,可认为接收信号的,则相位在[0,2π]内服从均匀分布,等效于z在[0,1/4]内服从均匀分布。而若雷达工作中心频率为500 MHz,带宽为50 MHz,雷达高度为 20 m,θ=1°,z的取值范围为0.55～0.61,z max-z min＜0.25·,此时,不能认为接收信号的相位在[0,2π]内服从均匀分布。所以,假设接收信号相位服从[0,2π]内均匀分布或者z服从[0,1/4]内均匀分布,雷达工作参数和工作场景需满足一定条件,具体可归纳为:

1)海面平静,目标掠射角足够低,可以满足反射系数近似为1;

2)反射波与直达波被同一波束接收;

3)雷达工作场景下z的取值范围为1/4的若干倍;

4)反射波与直达波的路程差小于雷达距离分辨单元。

在下面研究过程中,假定以上要求均能满足。

为了更加直观的理解多径效应对雷达接收信号的影响,图2给出了雷达接收信号矢量图。

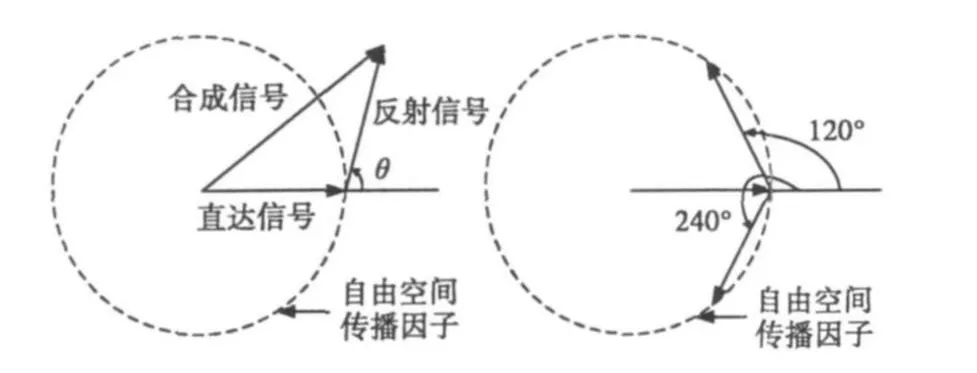
图2 雷达接收信号矢量图

从图2可以看出,当两矢量的夹角θ∈[-120°,120°]时,合成矢量幅度大于 1,目标信号被增强,当θ∈ [120°,240°]时 ,合成矢量幅度小于 1,目标信号被衰减。因此,多径散射对目标信号既有增强效果,又有衰减效果,但从统计的角度看,多径效应对雷达检测有利。

3.检测概率计算

直观上来看,多径条件下的雷达检测概率计算需建立在自由空间中雷达检测概率计算的基础上,飞机等起伏目标的检测概率计算要以非起伏目标的检测概率计算为基础,为此,首先研究自由空间中非起伏目标的雷达检测概率问题。

考虑自由空间中高斯白噪声环境下固定目标M-N检测,雷达接收信号y可表示为

式中:m=m～ejθ为目标回波信号;w为高斯白噪声,功率为β2.易得信噪比

在假设H0下,目标不存在,y=w,z=y 的概率密度为瑞利分布[12],即

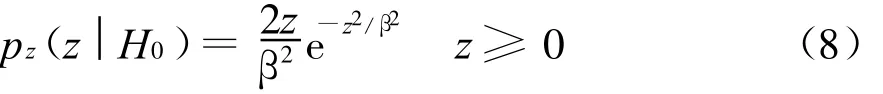
在假设H1下,目标存在,z服从莱斯分布,即

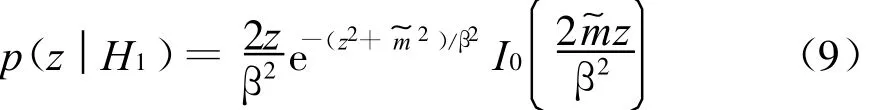
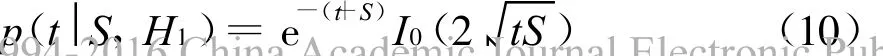
对式(10)关于t积分,可得单次检测概率

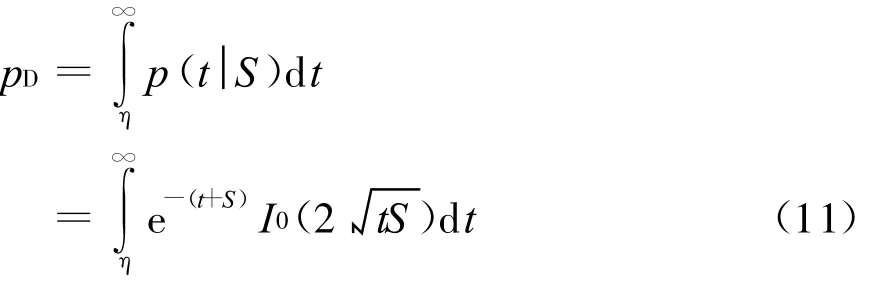
式中η为检测门限。

以上分析的是自由空间中的单次检测概率,针对多径环境下的起伏目标检测,由于存在镜面反射信号、目标雷达散射截面(RCS)起伏等特点,雷达接收信号幅度与传播因子、目标瞬时RCS有关,因此,检测概率与传播因子、平均信噪比、瞬时信噪比有关。为了得到多径条件下的检测概率,首先需要计算传播因子、回波信号幅度关于瞬时信噪比以及瞬时信噪比关于平均信噪比的概率分布函数。

定义功率传播因子μ为多径条件下雷达接收信号功率与自由空间中雷达接收信号功率之比。假定经归一化后的f(θr)=f(θd)≈1,则功率传播因子

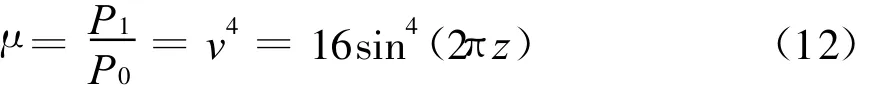
式中:P0为自由空间中雷达接收信号功率;P1为多径条件下雷达接收信号功率。

μ的概率密度为

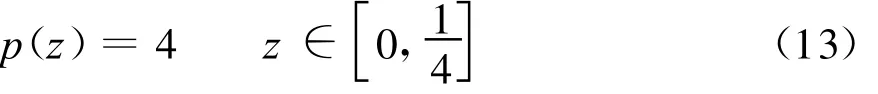
于是传播因子v的概率分布函数为

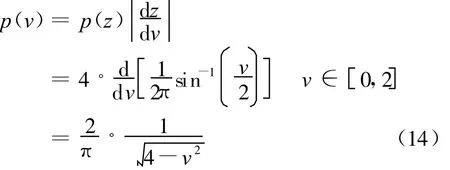
直达波和反射波叠加后的合成信号功率与传播因子v的四次方成正比[11],采用式(14)的方法可计算出功率传播因子μ的概率分布函数为

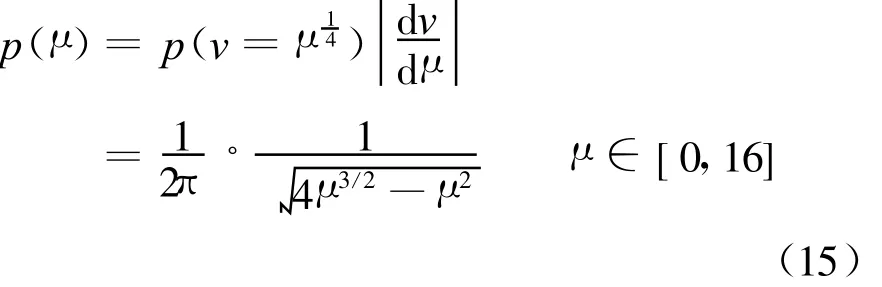
假设目标为RCS起伏服从SwerlingⅡ型分布的飞机,自由空间中,飞机的信噪比均值为S,瞬时信噪比为σ,则[8]

多径条件下飞机的瞬时信噪比为S′=μσ,其概率分布函数为

式中:Ω为功率传播因子μ的取值范围。

在S和μ已知的情况下,多径条件下目标瞬时信噪比的条件概率分布函数为

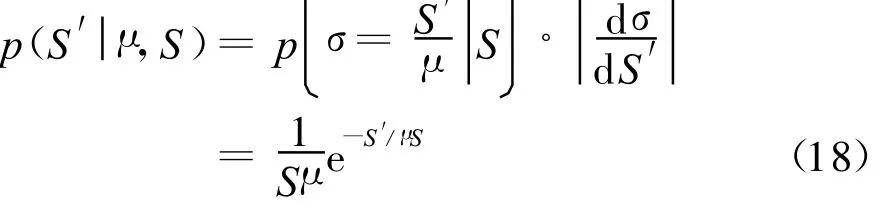
式(18)关于 μ积分,得到 μ未知、S已知情况下的目标瞬时信噪比的条件概率分布函数

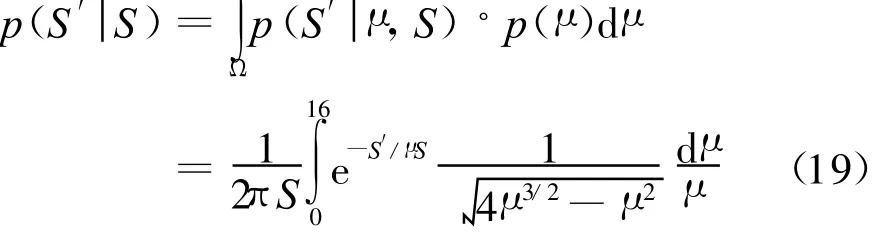
多径条件下雷达接收信号幅度关于平均信噪比S的条件概率分布函数可表示为

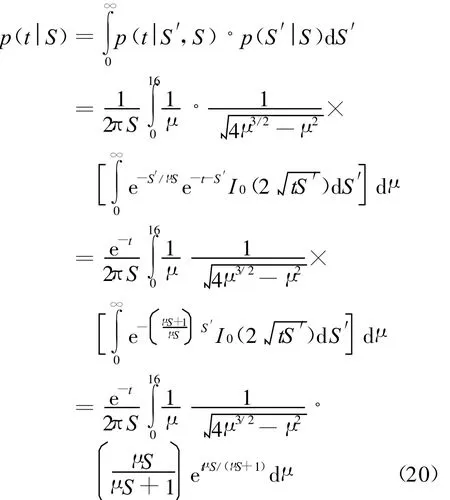
式(20)关于t积分,可得多径环境下的雷达单次检测概率

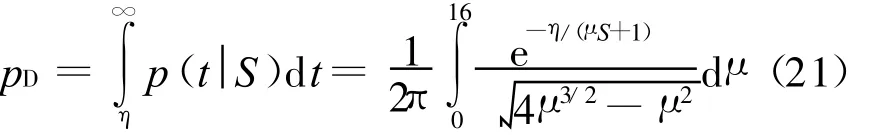
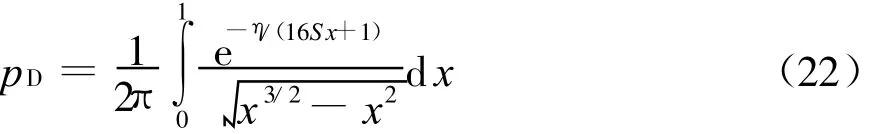
通过积分的方法很难得到p D闭合形式的解,在仿真中,采用复化辛普森公式对其进行数值积分。

最终N次检测概率为

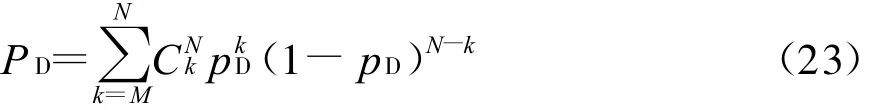
式中CNk为k组合。

4.仿真结果与分析

假设噪声归一化功率为1,在总的虚警概率一定的情况下,单次检测所允许的虚警概率p f可通过式(24)反推得到。

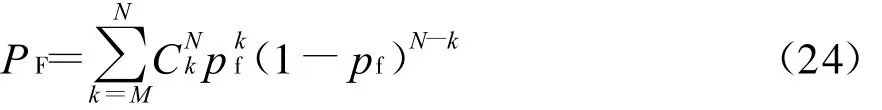
在求得单次检测的虚警概率之后,单次检测的门限η=-ln p f即可得到[12]。

为了更好的说明雷达在多径条件下的检测性能,在此,将雷达在自由空间中和在多径环境下的检测性能曲线进行了对比。其中,自由空间中的雷达单次检测概率为[12]

仿真分别给出了虚警概率PF=10-6、10-9,N=6、8时,雷达在两种不同环境下的检测概率曲线,如图3所示。图中实线、滑线、虚线、点滑线分别为M=1、2、3、4时的雷达检测概率曲线。

从图3可以看出,当M=1时,多径条件下的雷达检测性能都是最佳的,而且比自由空间中的雷达检测性能好,特别是在信噪比较低时,在相同的检测概率下,多径环境中检测所需的信噪比比自由空间中所需的信噪比低10 dB左右;随着信噪比的提高,相对自由空间,多径条件下的雷达检测性能优势逐渐减弱。对比图3(a)与(b)、(c)与(d)可以发现,在相同的虚警概率下,随着M、N值的变化,自由空间中的雷达检测性能变化不太明显,N值一定时,雷达最佳检测性能与M值之间没有明确的关系;但多径环境中的雷达检测性能对M、N值的变化比较敏感。N一定时,多径条件下的雷达检测性能随着M值的增大下降较快,且N越小,随着M值的增大,雷达检测性能下降越快。当M值较大时,随着信噪比的提高,多径条件下的雷达检测概率将低于自由空间中的雷达检测概率。在虚警概率和M值一定的情况下,N值越大,多径环境中的雷达检测性能越好。对比图3(a)与(c)、(b)与(d)可以看出:在检测器的M、N值一定时,相同信噪比下,两种环境下的雷达检测概率与虚警概率成正比。

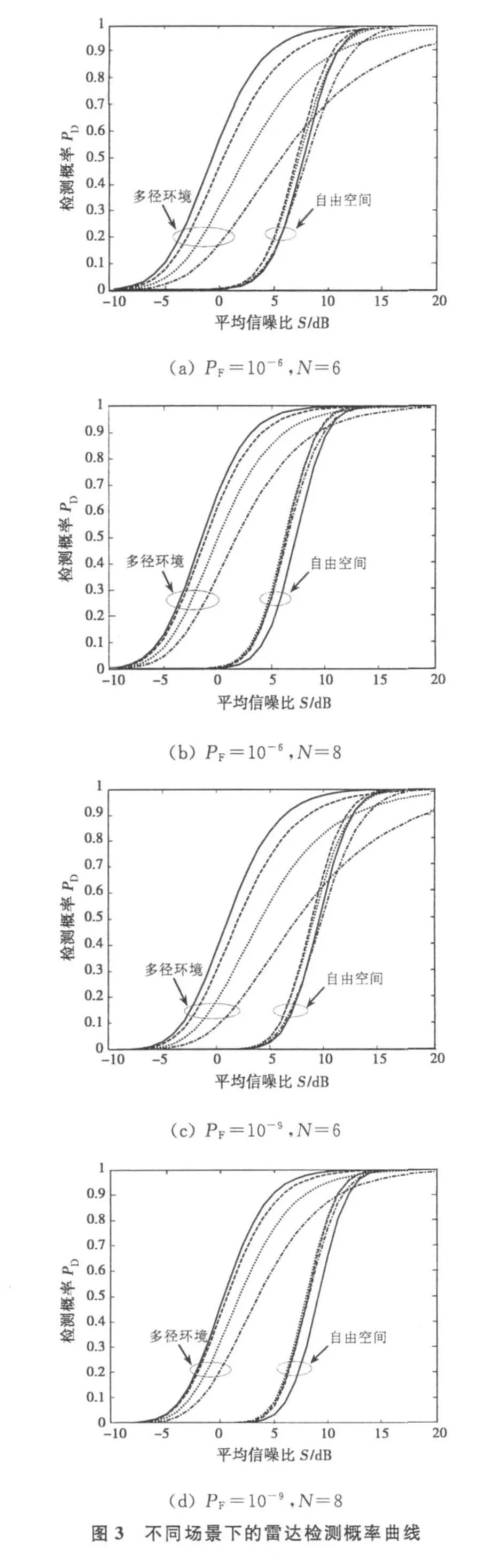
为此,若雷达工作在多径环境下,此时的雷达检测性能受M、N值影响明显,在设计 M-N检测器时,需选择最佳的M、N值以使雷达具有最佳的检测性能;而若雷达的工作环境多径效应不明显,此时的雷达检测性能受M、N值影响不大,在N值一定的情况下,应选择合适的M值以使雷达检测性最佳。为此,本文通过大量仿真总结出了不同环境、不同虚警概率下,雷达 N次探测时,雷达具有最佳检测性能时的最佳M值,如表1所示。

表1 不同条件下的最佳M值

从表1可以看出,多径环境下的最佳M值普遍比自由空间中的小。N取1～8时,多径环境下的最佳M值均为M=1;随着N值的增大,自由空间中的最佳M值也随之增大,但趋势缓慢。从表1还可以发现,虚警概率为10-6和10-9时的最佳M值相同。

5.结 论

通过理论推导与建模仿真相结合的方法,对雷达检测海面低空目标时的检测性能进行了分析,得到了在不同场景下M-N检测器具有最佳检测性能时的最佳M值,结果表明:从统计意义上来讲,低信噪比情况下,多径环境下的雷达检测性能优于自由空间中的检测性能;在 N一定的情况下,多径环境下的雷达检测性能对M值较敏感,自由空间中的雷达检测性能受M值的变化影响不大。为了使雷达在多径环境具有最好的检测性能,N取1～8时,最佳M值均为1。需要指出的是,文章的研究背景为平静海面低掠射角下的目标检测,多径散射以镜面反射为主,漫反射可忽略。通过实验数据对文中的结论进行验证是下一步作者即将展开的研究工作。

[1] WANG Xuezhi,MUSICKI D.Low elevation sea-surface target tracking using IPDA type filters[J].IEEE Trans on AES,2007,43(2):759-774.

[2] 周 围,朱联祥,周正中,等.相干多径环境下信号空间特征及波达方向估计[J].电波科学学报,2007,22(4):685-690.

ZHOU Wei,ZHU Lianxiang,ZHOU Zhengzhong,et al.Estimation of spatial signatureand direction of arrivals for signals in coherent multipath environment[J].Chinese Journal of Radio Science,2007,22(4):685-690.(in Chinese)

[3] 张 瑜,李玲玲.多径条件下雷达到达角的估算及仿真[J].电波科学学报,2004,19(2):215-218.

ZHANG Yu,LI Lingling.Radar arrived angle estimation and simulation under multi-path condition[J].Chinese Journal of Radio Science,2004,19(2):215-218.(in Chinese)

[4] 李 晶,裴 亮,曹茂永,等.一种多径环境的超分辨率TOA定位算法[J].电波科学学报,2006,21(5):771-776.

LI Jing,PEI Liang,CAO Maoyong,et al.Super-resolution TOA algorithm in multi-path environments[J].Chinese Journal of Radio Science,2006,21(5):771-776.(in Chinese)

[5] BARTON D K.Low-angle radar tracking[J].Proceedings of the IEEE,1974,62(6):687-704.

[6] BUCCO D,HU Yiding.A comparative assessment of various multipath models for use in missile simulation studies[C]//AIAA Modeling and Simulation Technologies Conference.Denver,USA,2000,1-10.

[7] SEN S,NEHORAI A.Slow-time multi-frequency radar for target detection in multipath Scenarios[C]//ICASSP 2010 Dallas,TX,USA,2010:2582-2585.

[8] WILSONS L,CARLSON B D.Radar detection in multipath[J].IEE Proceedings Radar,Sonar and Navigation,1999,146(1):45-54.

[9] GRAVES R H W.Detection of airborne targets by a space-based radar using multipath interference[C]//Proceedings of the 1991 IEEE National Radar Conference,Los Angeles,CA,USA,1991:46-49.

[10]TOUGH R JA,BAKER C J,PINK J M.Radar performance in a maritime environment:single hit detection in the presence of multipath fading and non-rayleigh sea clutter[J].IEE Procedings Radar and Signal:Processing,1990,137(1):33-40.

[11]焦培南,张忠治.雷达环境与电波传播特性[M].北京:电子工业出版社,2007:101-105.

[12]RICHARDS M A.Fundamentals of Radar Signal Processing[M].New York:Publishing House of McGraw-Hill,2005.