双基多输入多输出雷达快速目标空间定位算法

郭艺夺 张永顺 童宁宁 沈 堤

(空军工程大学导弹学院,陕西三原713800)

1.引 言

受多输入多输出(MIMO)通信发展及综合脉冲孔径雷达(SIAR:Synthetic Impulse and Antenna Radar)的启发以及雷达对新理论和新技术的需求,Fishler等人提出了MIMO雷达[1-2]的概念。MIMO雷达使用多个发射天线同时发射相互正交的信号波形照射目标,并使用多个接收天线接收目标反射的信号。因此,与MIMO通信系统类似,MIMO雷达系统对于目标的雷达散射截面(RCS)起伏不敏感,具有很好的目标检测性能[3]。此外,MIMO雷达可以实现灵活的发射信号波形设计[4],具有高分辨率的空间谱估计性能[5]。MIMO雷达的概念和信号处理技术受到了越来越多的关注。

MIMO雷达模型按发射阵列和接收阵列之间的配置方式可分为两大类:单基地MIMO雷达和双/多基地MIMO雷达。由于双基地MIMO雷达的回波信号中包含了目标相对于发射和接收阵列的角度信息,因此,可通过估计目标相对于发射和接收阵列的角度来实现对目标的交叉定位。针对双基地MIMO雷达的发射和接收角的估计,国内外学者提出了一些方法。文献[6]采用多信号分类(MUSIC)算法来估计目标相对于发射阵的发射角和接收阵的接收角,但需要二维谱峰搜索;文献[7]基于Capon(Minimum Variance Distortionless Response高分辨方位估计)方法实现了双基地MIMO雷达二维方位角的估计,该方法假设反射因子是任意的,且同样需要二维谱峰搜索;文献[8]采用旋转不变子空间方法把双基地MIMO雷达的二维方位角参数同时估计问题转化为两个一维方位角参数估计问题,分别采用两次信号参数估计(ESPRIT)方法同时估计出目标相对发射和接收阵列的方位角,不需要二维谱峰搜索;文献[9]中提出了一种双基地MIMO雷达的目标发射角和接收角联合估计的算法,该方法采用ESPRIT方法获得了目标发射角和接收角的闭式解,并可实现参数的自动配对。但以上算法都需要多周期目标回波才可实现对角度的正确估计,且上述算法都只考虑了目标相对于发射和接收阵列的一维角,因而不能实现对目标的空间定位。

文中基于双基地MIMO雷达系统,提出了一种快速的多目标空间定位算法。文中建立了双基地MIMO雷达的信号模型,并通过理论推导导出了目标空间坐标的闭式解。该算法避免了数据协方差矩阵的估计,不需要多维谱峰搜索和参数配对,在保证参数估计性能的基础上,降低了算法的计算量。

2.双基地MIMO雷达信号模型

考虑一发射和接收阵列均采用L型配置的双基地MIMO雷达系统,其中发射阵元数为3,分别位于坐标原点、X轴和Y轴上,各发射阵元同时发射同频相互正交的相位编码信号,即满足

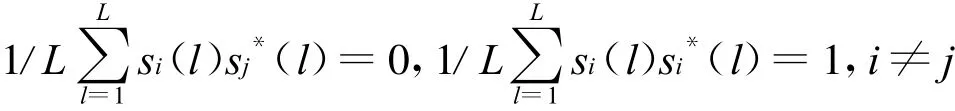
且i,j=1,…,3,L为在每个发射信号重复周期内的相位编码个数;接收阵元总数为Mr(Mr=Mr1+Mr2+1,其中位于X轴上的接收阵元数为M r 1,位于Y轴上的接收阵元数为Mr2,位于接收阵原点的阵元数为1),且发射和接收阵元间距均为λ/2(λ为载波波长)。设发射阵和接收阵之间的基线距离为D,且满足D≫λ,并假设在雷达系统的远场同一距离单元内存在N个目标,其与发射阵的X轴,Y轴和Z轴正方向的夹角为αti,βti,γti,与接收阵的 X 轴,Y′轴和Z′轴正方向的夹角为 αri,βri,γri(i=1,2,…,N),且 αti,βti,αri,βri ∈[0,π),γti,γri∈[0,π/2),如图1所示。可以证明 αti,βti,γti,αri,βri,γri满足如下关系

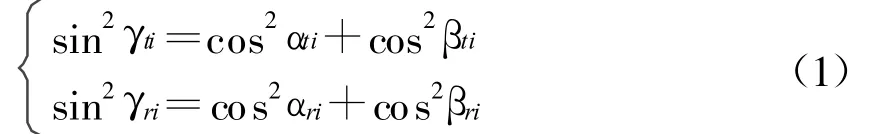
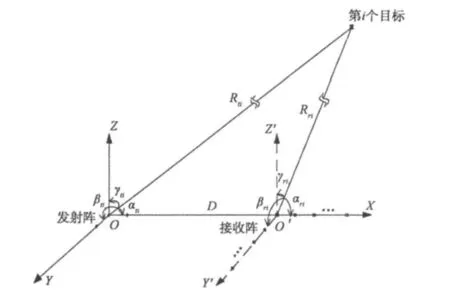
图1 双基地MIMO雷达模型

因此,位于X轴和Y′轴的接收阵列的单周期回波信号可分别表示为

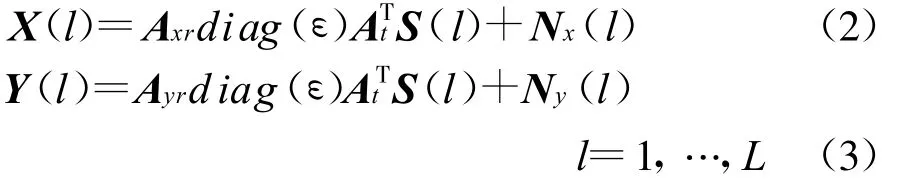
式中 :Axr=[axr(αr1),…,axr(αrN)],axr(αri)为位于X轴的接收阵列对应于第i个目标的导向矢量,a xr(αri)=[1,exp(-jπcosαri), …,exp(-jπMr1 cosαri)]T;A yr=[a yr(βr1),…,a yr(βnN)],a yr(βri)为位于Y轴的接收阵列对应于第i个目标的导向矢量 ,ayr(βri)=[1,exp(-jπcosβri),…,exp(-jπMr2cosβri)]T;A t=[a t(αt1,βt1),…,a t(αtN,βtN)],a t(αti,βti)为发射阵列对应于第i个目标的导向矢量,a t(αti,βti)=[1,exp(-jπcosαti),exp(-jπcosβti)]T;ε=[ε1,…,εN],εi是与第 i个目标的 RCS 相关的复数,diag(ε)表示由矢量ε形成一对角阵;S(l)=[s1(l),s2(l),s3(l)]T为发射信号矢量;Nx(l)和Ny(l)为加性高斯白噪声。上标T表示矩阵的转置。

3.所提算法

3.1 虚拟阵列的形成

因为MIMO雷达发射信号是相互正交的,所以用位于X轴和Y轴的阵列接收数据分别与3个发射信号进行匹配滤波,即可得到6个与发射信号相对应的虚拟阵列

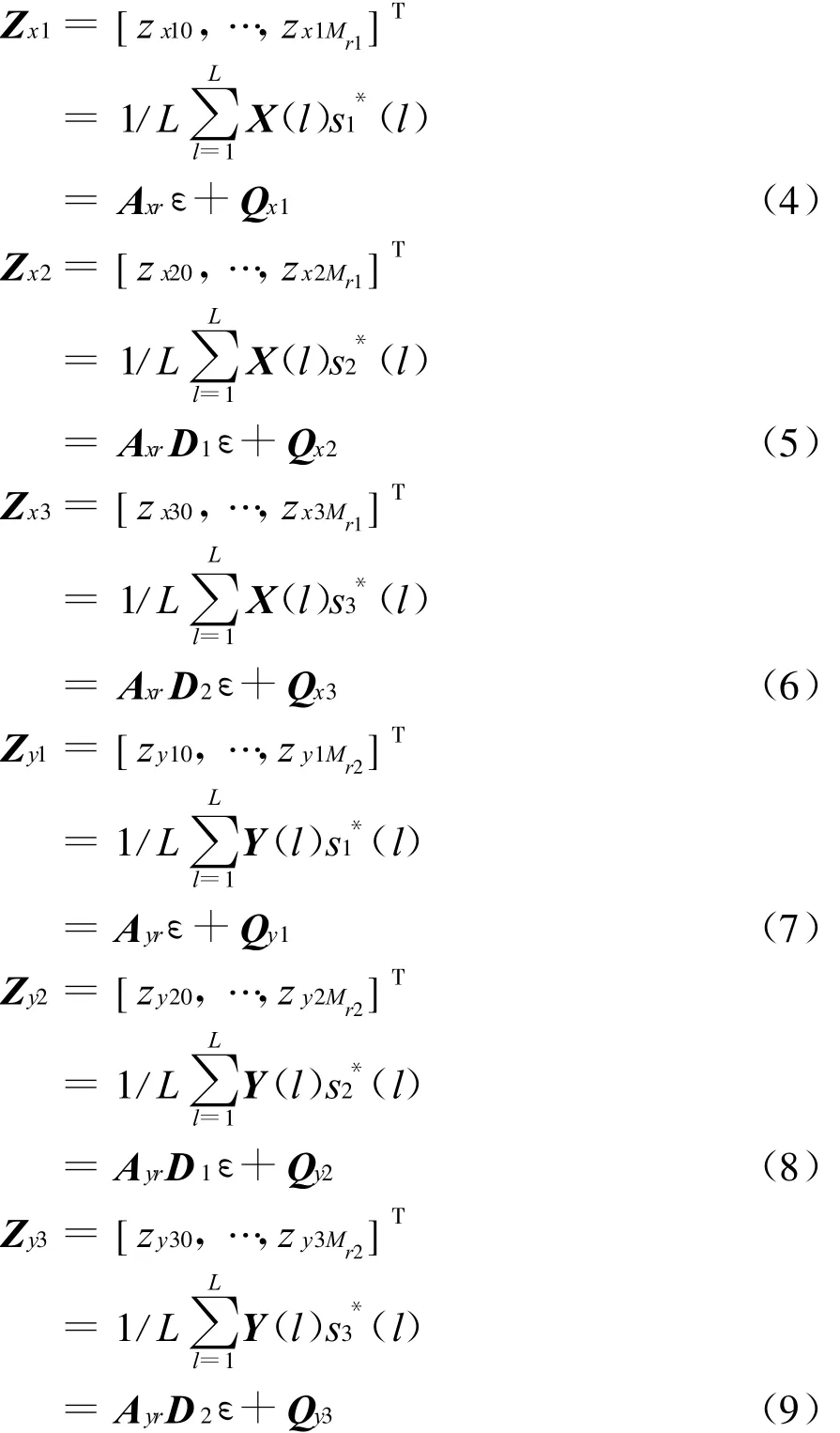
式中 :D1=diag{[exp(-jπcosαt1),…,exp(-jπcosαtN)]};D2=diag{[exp(-jπcosβt1),…,exp(-jπcosβtN)]};Q xi=1/L(l)(i=1,2,3)为各虚拟阵列的噪声,且均为高斯白噪声;上标*表示取共轭。

3.2 目标角度的估计

由式(4～9)可以看出:对于各虚拟阵列来说,目标信号是完全“相干”的。因此,要得到对目标角度的正确估计,必须先进行“解相干”处理。

假设存在p分别满足1≤p≤min(Mr1,Mr2),且p≥N,定义如下选择矩阵J k及J′t

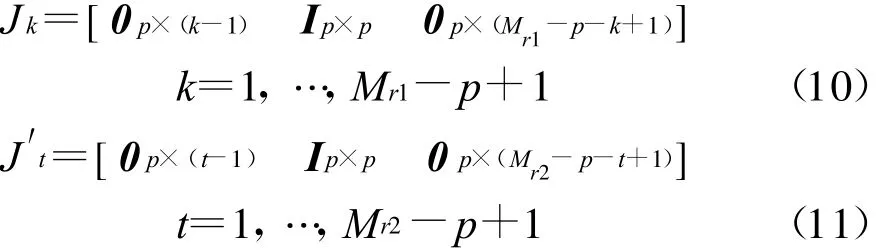
式中 :0p×(k-1)为 p ×(k-1)维的全 0 矩阵 ;Ip×p为p×p的单位阵。

首先构造如下矩阵

式中,JMr1和JMr2为反对角线上元素全为1,其它位置全为0的Mr1×M r1和 Mr2×Mr2的置换矩阵。

由式(12～15)可构造如下矩阵

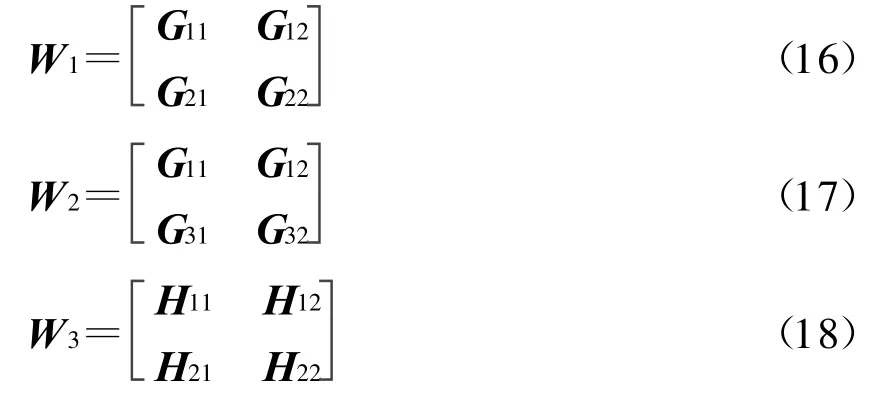
将(4～9)式代入式(16～18)可得

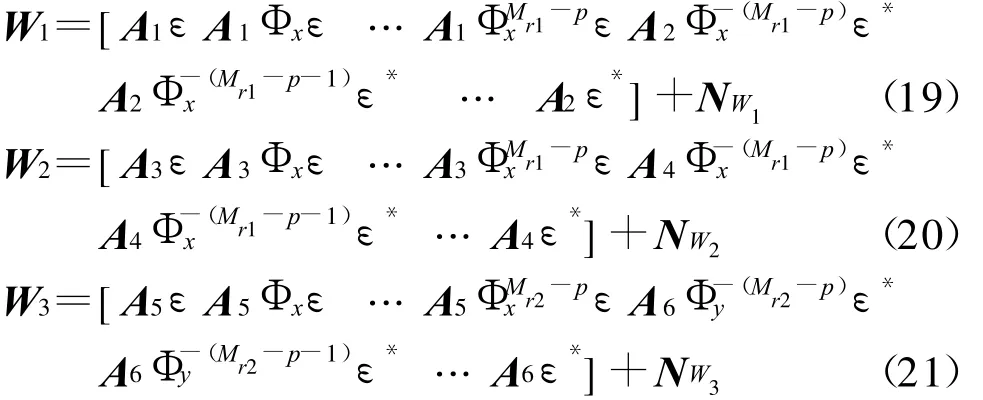
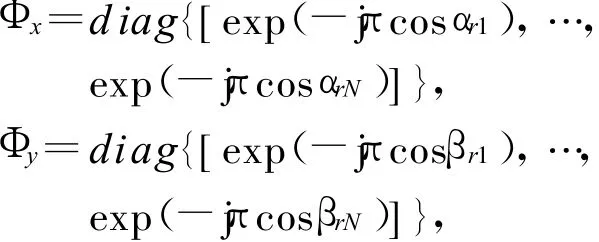
同时可以验证 A1和 A2、A3和 A4及A5和 A6分别满足

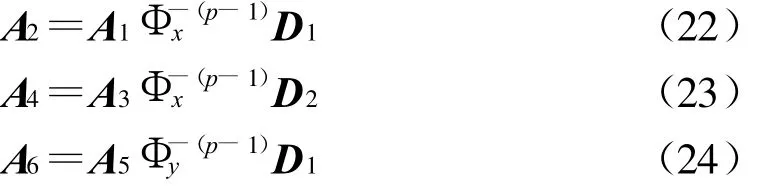
将式(22～24)分别代入式(19～21)可得

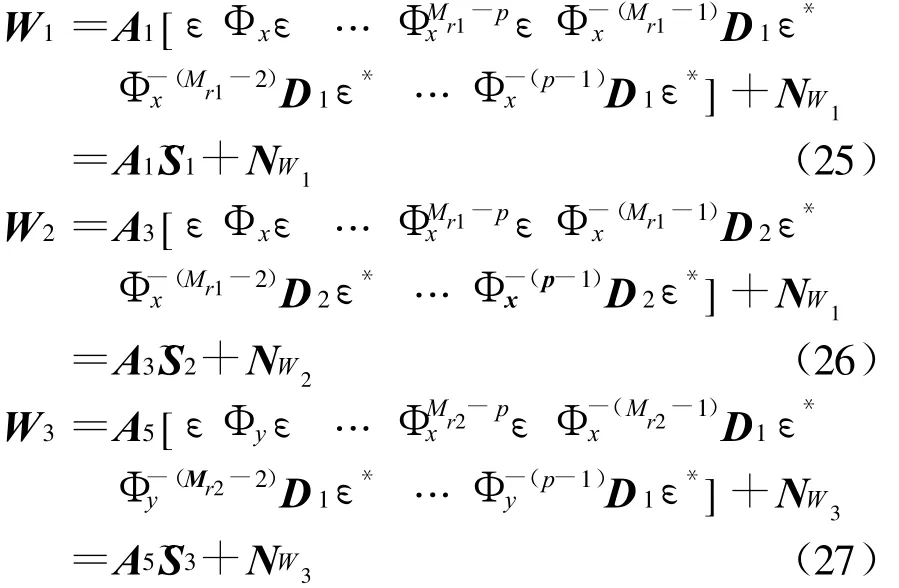
可以证明:当满足2(Mr1-p+1)≥N及2(Mr2-p+1)≥N 时,有 rank(～S1)=rank(～S2)=rank(～S3)=N,即实现了对所有目标信号的“解相干”。

为了减小计算量并构造三个具有特定关系的矩阵,这里采用传播算子法对W1、W2和W3进行处理。设A11和A12分别为A1的前N 行和后2p-N行,则存在矩阵VH1((2p-N)×N维)使得下式成立

称VH1为传播算子[10]。记的前N行和后2p-N 行为W11、W12。不考虑噪声影响时,有

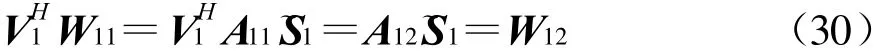
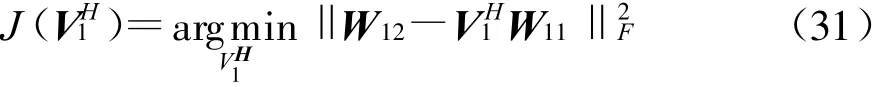
式中‖·‖F表示Frobenius范数。求解上式可得

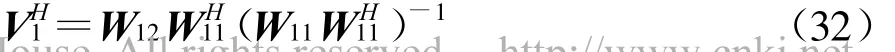
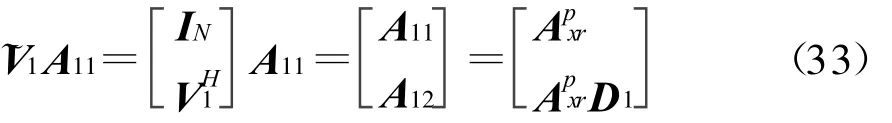
由式(33)可知,～V1可张成信号子空间。分别记 ～V1的前 p行和后 p行为和,有=及～V12A11=ApxrD1,因此 ,可得[10]

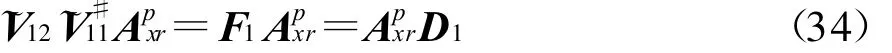
若分别记W2和W3的前 N行和后2p-N行为及、,=()-1;,且～V21、～V22及～V31、～V32分别为 ～V2和 ～V3的前 p行和后p行。同理可得

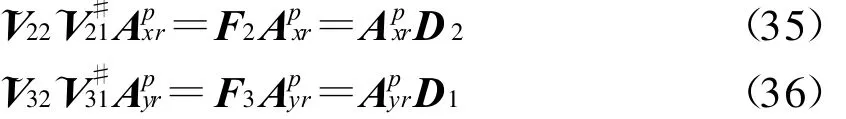
从式(34～36)可以看出:F1和F2有相同的特征向量矩阵,而F1和F3有相同的特征值矩阵。对F1和F3进行特征值分解可得 N个大特征值λ1,λ2,…,λN,其对应的特征向量分别为e1,e2,…,e N及,e′2,…,e′N.由和Apyr的表达式可知

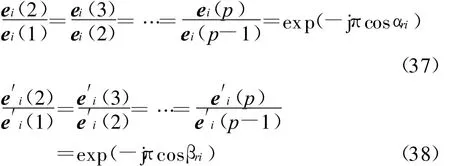
式中:arccos表示反余弦函数;sum表示矢量求和;angle表示求相位角。

由式(35)可知:要得到对 βti的估计,只需获得F2的特征值即可。因此,为了减小计算量且实现对目标参数的自动配对,可以采用如下方法来估计F2的第i个特征值

βti的估计值为

3.3 目标的空间定位

在得到对 ^αri、^βri、^αti及 ^βti的估计后 ,根据式(1),可得和的估计值 。

如图1所示,由正弦定理可得

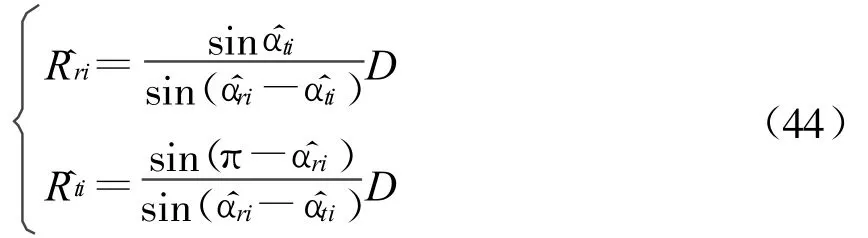
根据图中的几何关系,可得目标在空间中的三维坐标为

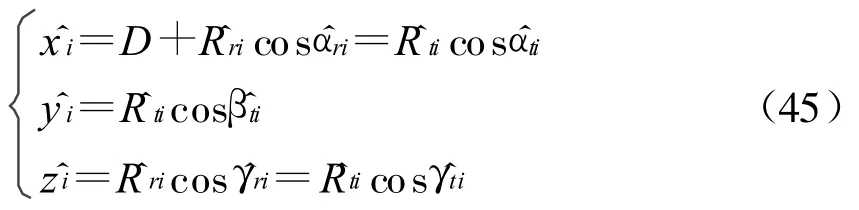
从而实现了对目标的定位。

4.计算机仿真结果

为了验证本文算法的有效性,做如下计算机仿真。仿真过程中假设基线距离D=50 km.

仿真1:算法对目标角度估计及空间定位结果

从表1和图2可以看出:本文所提算法能较为精确地估计出目标相对于发射阵和接收阵的角度,从而可较为精确地实现对空间目标的定位。

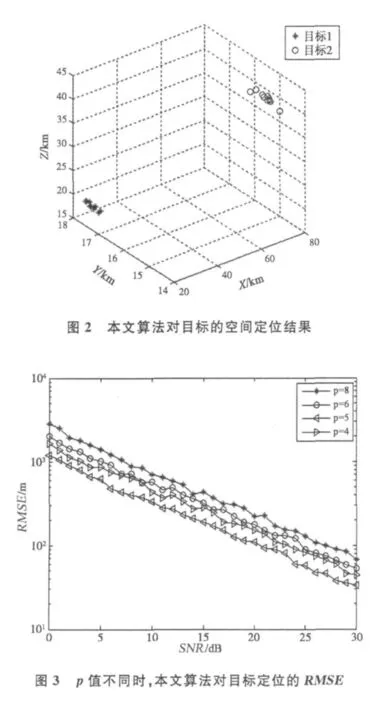
仿真2:p值不同时,本文算法对目标空间定位的均方根误差(RMSE)

仿真条件设置同仿真1,图3中给出了p值取为8,6,5,4时,本文算法对第一个目标进行空间定位的RMSE。图中信噪比从0 d B按步长1 d B变化到30 d B,仿真结果为100次Monte-Carlo实验(每个SNR点做100次Monte-Carlo仿真)的统计结果。定义对第i个目标空间定位的RMSE为

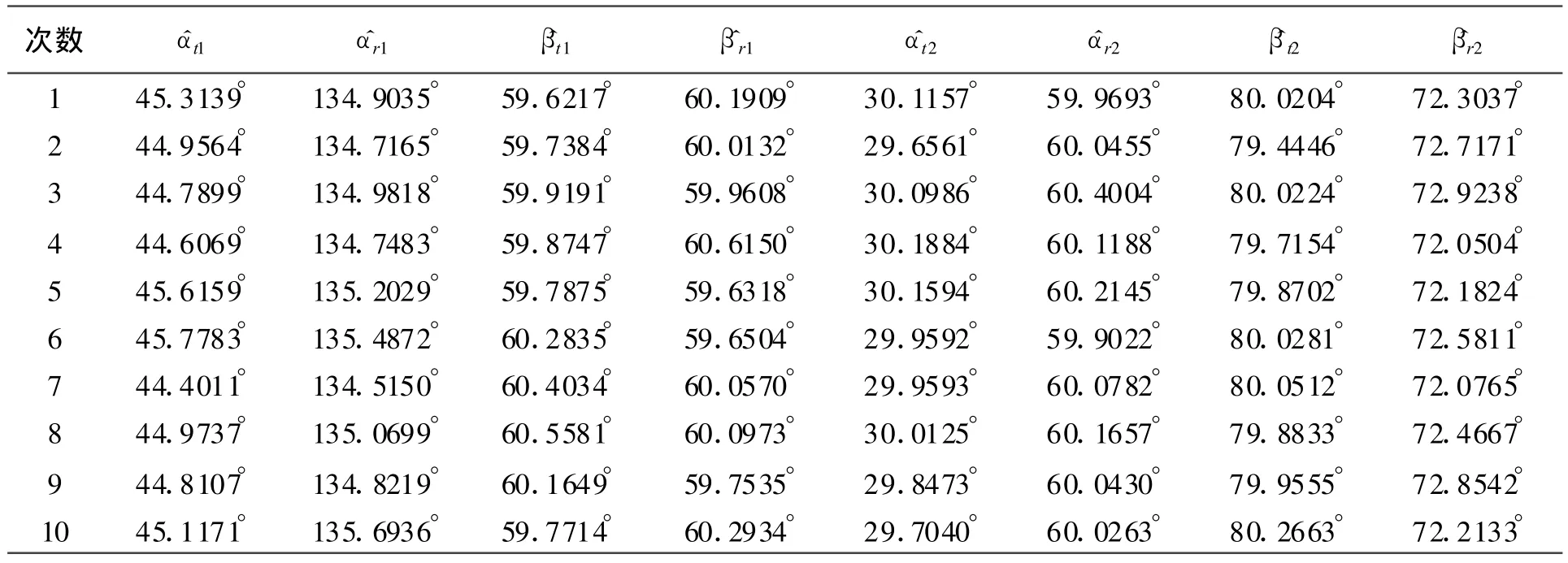
表1 算法对目标角度的估计值

其中xi,yi和zi为目标对应的真实位置。

从Monte-Carlo仿真结果可以看出:p=5时,本文算法的统计性能最好,这主要是因为在单周期目标回波的情况下,对于每个虚拟阵列来说,所有目标都是“相干”的,随着 p值的减小,“解相干”的效果越好,然而p值越小阵列的有效孔径损失得越严重。因此,算法的“解相干”效果和阵列的有效孔径之间存在着矛盾,当p为大于目标数而小于接收阵元数的某一数值时,本文算法的性能达到最优。然而,总体看来,不论p取何值,本文算法都具有较好的统计估计性能。

5.结 论

针对空间目标的精确定位问题,提出了一种基于双基地MIMO雷达的快速目标空间定位算法。理论和计算机仿真结果表明:所提算法避免了数据协方差矩阵的估计,不需要多维谱峰搜索和参数配对,大大降低了运算复杂度。此外,该算法只需单周期回波信号即可实现对目标相对于发射阵和接收阵角度的估计,这使得其非常适合于瞬时目标信号和快速运动目标信号的来波方向估计。

[1] FISHLER E,HAIMOVICH A,BLUM R,et al.MIMO radar:an idea whose time has come[C]//Proceedings of the IEEE Radar Conference,Newark,NJ,USA,April 2004,71-78.

[2] 何子述,韩春林,刘 波.MIMO雷达概念及其技术特点分析[J].电子学报,2005,33(12A):143-147.

HE Zishu,HAN Chunlin,LIU Bo.MIMO radar and its technical characteristic analyses[J].Acta Electronica Sinica,2005,33(12A):143-147.(in Chinese)

[3] 曾建奎,何子述.慢起伏目标的多输入多输出雷达检测性能分析[J].电波科学学报,2008,23(1):158-161.

ZENG Jiankui,HE Zishu.Analysis of MIMO detection performance for slow fluctuating target[J].Chinese Journal of Radio Science,2008,23(1):158-161.(in Chinese)

[4] 刘韵佛,刘 峥,谢 荣.一种基于拟牛顿法的MIMO雷达发射方向图综合方法[J].电波科学学报,2008,23(6):1188-1193.

LIU Yunfo,LIU Zheng,XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on Newtonlike method[J].Chinese Journal of Radio Science,2008,23(6):1188-1193.(in Chinese)

[5] LEHMANN H,FISHLER E,HAIMOVICH M,et al.Evaluation of transmit diversity in MIMO-radar direction Finding[J].IEEE Trans.Signal Processing,2007,55(5),2215-2225.

[6] LI J,CONAN J,PIERRE S.Joint estimation of channel parameters for MIMO communication systems[C]//2nd International Symposium on Wireless Communication Systems,2005,22-26.

[7] YAN Haidong,LI Jun,LIAO Guisheng,Multitarget identification and localization using bistatic MIMO radar systems[J].EURASIP Journal on Advances in Signal Processing,2008,8(2):1-8.

[8] CHEN Duofang,CHEN BaiXiao,QI Guodong.Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12):770-771.

[9] JIN Ming,LIAO Guisheng,LI Jun.Joint DOD and DOA estimation for bistatic MIMO radar[J].IEEE Trans.Signal Processing,2009,89(2):244-251.

[10] 任勋立,廖桂生,曾 操.一种低复杂度的二维波达方向估计方法[J].电波科学学报,2005,20(4):526-530.

REN Xunli,LIAO Guisheng,ZENG Cao.A low complexity method for estimating 2-D DOA[J].Chinese Journal of Radio Science,2005,20(4):526-530.(in Chinese)