低密度奇偶校验码差分跳频系统的抗干扰性能

朱毅超 甘良才 熊俊俏

(1.中国舰船研究院,北京100192;2.武汉大学电子信息学院,湖北 武汉430079)

1.引 言

差分跳频技术是近十年间所出现的一种新型跳频体制,它通过生成函数G使相邻跳频率之间具有相关性,并利用这种相关性传递信息,从而使系统具有一定的误跳纠正能力[1-3]。窄带干扰是军事通信中重要的人为干扰,它对通信系统性能的影响十分突出[4]。部分频带干扰是一种主要的窄带干扰类型,文献[5][6]分别采用联合-切尔诺夫界与联合界的方法对无编码差分跳频系统抗部分频带干扰的性能进行了分析。由于纠错编码技术可以显著地提高传统跳频系统的抗干扰能力[4],因此,研究其对差分跳频系统抗干扰性能的改善具有一定的理论和实际意义。

低密度奇偶校验(LDPC)码是近年来编码领域的研究热点,它是一种性能接近香农限而且可以实现的编码方案,其性能有时甚至可以超过 Turbo码[7-8]。文献[9]将基于GF(q)(q＞2)的LDPC码应用于差分跳频系统,对其在加性白高斯噪声(AWGN)信道下的比特误码率(BER)进行了数值仿真,但却并未考虑干扰的影响。拟将非规则二进制LDPC码作为差分跳频系统的纠错码,并在部分频带干扰信道下对其进行优化,研究优化后的LDPC码对系统抗干扰性能的改善。

2.LDPC码及LDPC码差分跳频系统模型

LDPC码是一种线性分组码,可由它的校验矩阵来定义,其校验矩阵是一个稀疏矩阵。此外,LDPC码还可以用双向图来表示,如图1所示。该图与校验矩阵直接对应,图中方形节点为校验节点,每个节点代表一个校验方程或校验矩阵中的一行;圆形节点为变量节点,每个节点代表码字中的一个比特或校验矩阵中的一列。当校验矩阵中的某一元素值为1时,对应的校验节点与变量节点间存在连线。对于每个节点,与之相连的边数称为该节点的次数。

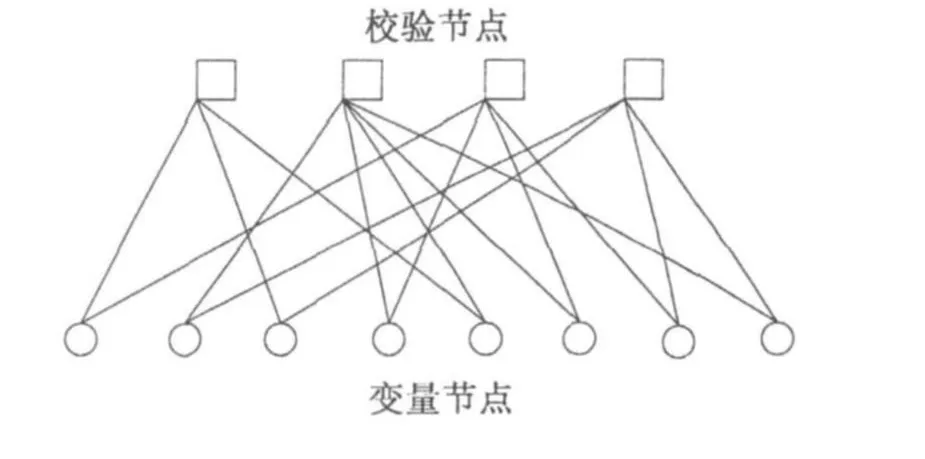
图1 LDPC码双向图

LDPC码变量节点与校验节点的次数分布由多项式

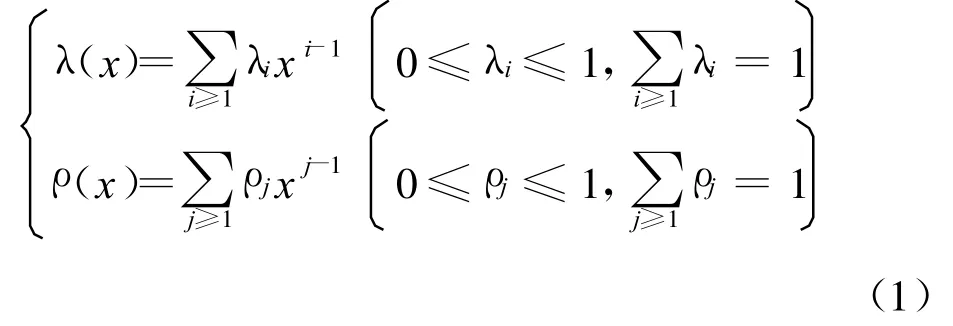
表示,且满足

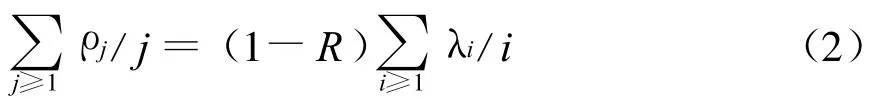
式中:系数λi与ρj分别表示LDPC码双向图中与次数为i的变量节点及次数为j的校验节点相连的边数占总边数的比;R为LDPC码的设计码率。

若LDPC码的校验矩阵是满秩的,则R就是该码的实际码率,否则R小于该码的实际码率。若{}与}中均只有一个元素为1,其余元素均为零,则该码为规则LDPC码,反之则为非规则LDPC码。

LDPC码差分跳频系统框图如图2所示。信息比特经LDPC编码后送入G函数单元产生发送频率号,多频制(MFSK)调制器根据发送频率号确定相应的频率并发送。在接收端,软输入软输出(soft input-soft output,SISO)内译码器检测所有可用频点上的信号能量,并结合LDPC变量节点(即编码比特)译码器的输出外信息LV对LDPC编码比特进行SISO译码,计算每个编码比特的后验概率LS.LDPC变量节点译码器利用LS及LDPC校验节点译码器的输出外信息LB,对每个变量节点的后验概率进行更新。LDPC校验节点译码器利用更新后的变量节点后验概率LA,根据校验方程计算下次迭代时输出到变量节点译码器的外信息LB,而变量节点译码器则利用LB计算下次迭代时输出到SISO内译码器的外信息L V.

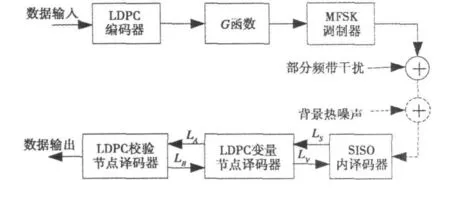
图2 LDPC码差分跳频系统框图

SISO内译码器所采用的SISO译码算法与Turbo码分量码译码器所采用的译码算法相同,详见文献[10]。下面简要说明LA、LB及LV的计算方法,假设它们均为对数似然比(log-likelihood ratio,LLR)形式lg(p 0/p 1),p0与p 1分别为比特取值为0与1的概率。令L(m)≡{l,Hml=1}表示与校验节点m相连的变量节点集合,其中 Hml为校验矩阵第m行第l列的元素,令M(l)≡{m,H ml=1}表示与变量节点l相连的校验节点集合,令L(m)l表示在集合L(m)中除去变量节点l,令M(l)m表示在集合M(l)中除去校验节点m,则由变量节点l输出到校验节点m的外信息LlmA可计算为

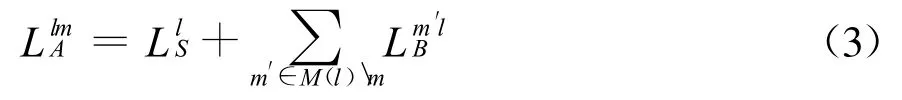
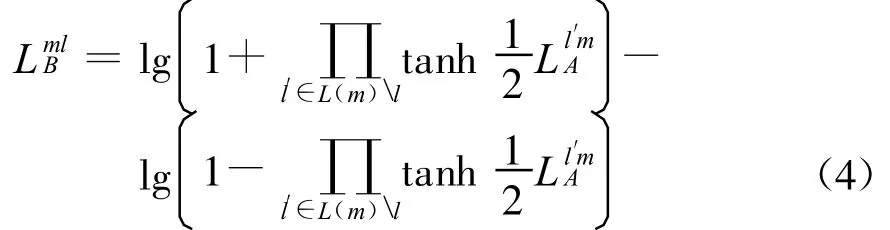
式中:tanh(x/2)≡(ex-1)/(ex+1),x为变量节点的对数似然比。

在译码开始时,先将LV的初值设为零,随后在每次迭代过程中,依次计算LS、LA、LB及LV.同时在每次迭代过程中,变量节点译码器计算编码比特l的总似然比信息

根据LT对每个编码比特进行硬判决,并利用校验矩阵判断硬判决后得到的码字是否为有效的LDPC码字,若是,则译码结束,否则继续迭代译码直到达到预设的迭代次数,若此时仍无法得到有效的LDPC码字,则译码失败。

部分频带干扰可以模拟为加性高斯噪声,假设所有可用频率数为M,干扰机将总的噪声功率均匀分布在n(n≤M)个跳频子频带内,因此,任一特定频率上存在干扰的概率为ρ=n/M,而不存在干扰的概率为1-ρ.令NJ为差分跳频总带宽内的平均干扰单边功率谱密度,则在存在干扰的子频带内,干扰单边功率谱密度为 NJ/ρ,而在不存在干扰的子频带内,干扰单边功率谱密度为0。同时若系统存在背景热噪声,则将其模拟为单边功率谱密度为N 0的全频带加性白高斯噪声。分析中不考虑信道衰落的影响。

差分跳频系统的性能主要取决于其G函数网格图的最小自由距离d free[3]。若系统每跳传输1比特,则 dfree的最大值为 lb M,它可由生成矩阵为[1,D,D2,…,DlbM-1]的正交卷积码实现[3]。然而,若将LDPC码作为外码,G函数作为内码组成串行级联码,则由文献[11]可知,内码应为递归码,因此,将M=8,生成矩阵为[1,D,D2]/(1+D2)的二进制递归正交码作为 LDPC编码差分跳频系统的G函数。

3.有干扰状态信息时编码系统的抗干扰性能

文献[4]指出,若要使跳频系统具有良好的抗部分频带干扰能力,系统必须得到精确的干扰状态信息(JSI)。对于差分跳频系统而言,即接收端必须知道所有可用频点上是否存在干扰。若差分跳频系统跳速足够高,使得干扰状态在连续h(h＞1)跳中保持不变,且系统可以确保在该h跳内不会发送同一频率,则当背景热噪声不存在时,系统根据所有可用频点上的输出能量即可得到精确的JSI,其方法为:对每跳接收信号定义观测向量v={v1,v2,…,vM},若该跳接收信号在频率 f i(1≤i≤M)上的输出能量不为零,则v i=1,否则v i=0。在每跳信号接收后,均将该跳的观测向量与前一跳进行比较,若两跳的观测向量不同,则在两个观测向量中值均为1的元素所对应的频率即为h跳中的被干扰频率,若所有h跳的观测向量均相同,则所有观测向量中值为1的元素所对应的频率为被干扰频率。

表1 编码系统对不同干扰频率数n的优化节点次数分布

在不存在背景热噪声的情况下,SISO译码器可以采用加权能量度量作为译码度量。若令r={r 1,r2,…,rM}表示所有可用频率上的非相干能量检测输出,则加权能量度量可表示为

式中:x为发送频率号;r x为对应频点上的输出能量值;z为干扰状态变量,z=1表示该频点被干扰,z=0表示该频点未被干扰;c(z)为加权函数,且c(0)的取值应远大于c(1)[4]。

若所有可用频率均被干扰,则SISO译码器可以采用最优的极大似然度量来代替加权能量度量。极大似然度量为[12]

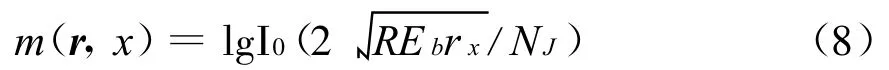
式中:Eb为信息比特能量;I0(·)为第一类零阶修正贝塞尔函数。

为了让非规则LDPC码达到最佳性能,需要针对不同的调制方式及信道条件对其进行优化,两种主要的优化方法为密度进化算法与外信息转移(extrinsic information transfer,EXIT)图方法[13-14]。密度进化算法通过计算每次迭代后变量节点取值似然比的概率密度函数,寻求变量节点与校验节点的最优次数分布,使得LDPC码可以用最少的迭代次数达到给定的误码率,或在相同的迭代次数下误码率最小。然而,对于差分跳频系统的SISO译码器,无法得到其输出外信息的概率密度函数表达式,采用仿真及直方图的方法虽然可得到离散的概率密度函数,但由于每次迭代后SISO译码器的输出外信息均不同,优化过程需要对SISO译码器进行多次仿真,耗时太多,因此,密度进化算法不适用于LDPC编码差分跳频系统。EXIT图方法将输出外信息近似为高斯分布,计算变量节点译码器与校验节点译码器的EXIT曲线,搜索最优的变量节点与校验节点次数分布,使得两条EXIT曲线间的通道在尽可能低的信噪比时仍然开启。该方法在优化过程中只需对SISO译码器进行一次仿真,从而大大减少优化所需的时间,适用于LDPC编码差分跳频系统。文献[15]给出了具体的优化算法,这里不再赘述。

在干扰频率数 n=6、7、8的部分频带干扰下,采用式(7)及式(8)给出的译码度量,对变量节点次数为 2、3、4,校验节点次数为 3、4、8、12 的非规则LDPC码差分跳频系统进行优化后的节点次数分布如表1所示。LDPC码的性能主要由其变量节点的次数分布决定[13]。从表1可见,由于对不同的n,变量节点次数的分布大致相同,因此,考虑以n=8的节点次数分布作为优化LDPC码的节点次数分布。

一般来说,编码系统可以通过联合界计算极大似然译码的误码率(BER)上界,其关键是寻求码的重量分布。然而对于LDPC码来说,根据某个具体的校验矩阵,寻求其码重分布是十分困难的,通常只能由校验矩阵的构造方法,寻求一类LDPC码的集合平均码重分布。文献[16]给出了规则LDPC码的集合平均码重分布的上界,其计算思路也可扩展到非规则 LDPC码。然而,根据此码重上界,只能得到以多项式形式下降的集合平均BER上界,而无法得到以指数形式下降的BER上界,这说明其上界与实际值的差距较大,不够精确。若采用与优化算法相同的思路,将译码器的输出外信息近似为高斯分布,由于高斯分布的似然比变量,其方差为均值的两倍,因此,只需计算各次迭代后节点似然比外信息的均值,即可得出其概率密度函数,并可通过它计算各次迭代后的集合平均BER。该方法只需对SISO译码器进行一次仿真,计算复杂度较低,但该方法假设LDPC码的双向图中不存在短循环,这是码长为无限长时的理想状况,显然该方法得到的BER可以作为实际BER的渐近下界。

采用高斯近似的校验节点似然比信息,其均值的更新公式为[17]

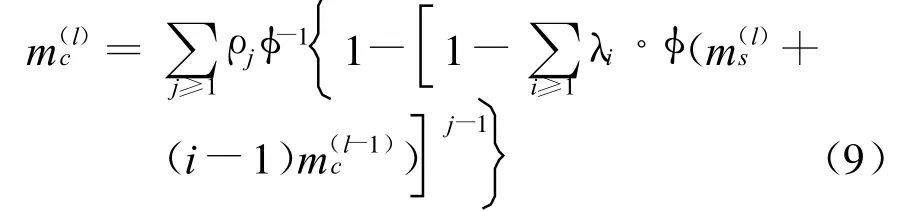
式中:m(l)c为第l次迭代后校验节点外信息的均值,m(0)c设为零;m(l)s为第l次迭代后SISO译码器的输出外信息的均值,它可以由SISO译码器的 EXIT图得到;函数φ(x)定义为

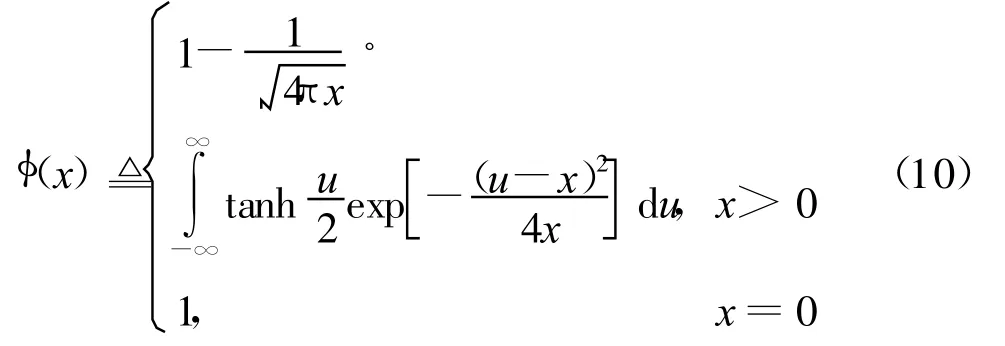
l次迭代后的集合平均BER为

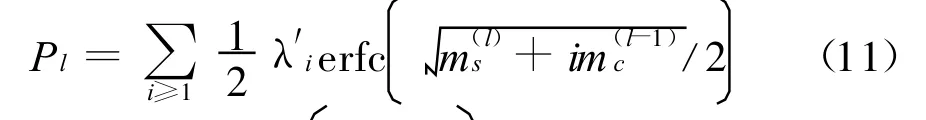
4.无干扰状态信息时编码系统的迭代干扰估计及译码算法

若差分跳频系统中存在背景热噪声,则系统无法得到精确的JSI,为使系统仍具有抗窄带干扰能力,必须对其进行估计。一种好的方案是将JSI估计与迭代译码结合起来,在每次迭代过程中对JSI的估计进行更新,使其精确度逐渐提高,并采用这种逐步更新的JSI进行译码,经多次迭代后,可以趋近于存在精确JSI的理想情况,从而保证了系统的抗干扰能力。

差分跳频系统的JSI为所有可用频点上的干扰状态,若系统总频点数为M,其中n个频点上存在干扰,则最优译码应对种可能的干扰分布均进行估计,显然当M较大时,可能的干扰分布数过多,译码复杂度过高。为了解决此问题,提出了一种次优算法,借助导频信号对每个频点上的干扰状态进行估计,并将其作为迭代估计的初值,从而将各个频点上的干扰状态独立开来,大大地降低了计算复杂度。

该算法假设接收机已知信道噪声的功率谱密度,即任一频点被干扰时的噪声功率谱密度σ21=NJ/2ρ+N0/2,以及未被干扰时的噪声功率谱密度σ20=N0/2。同时,假设差分跳频的跳速足够高,使得干扰状态在连续h+1跳内保持不变,于是系统每隔h跳发送一跳导频信号,用来估计每个频点上的干扰状态初值。在接收端,SISO译码器首先对所有的导频信号进行非相干解调,根据其输出计算干扰状态初值,并将该初值作为首次迭代时的干扰状态先验信息。在每次迭代过程中,将前次迭代的各频点上的干扰状态作为先验信息,并利用信道的记忆性,结合所有h跳的非相干解调输出,计算本次迭代的各频点上的干扰状态,再利用其计算译码时的G函数网格图分支度量。整个过程具体阐述如下。

令F≜{f 1,f 2,…,f M}为系统可用频率集,不失一般性,假设所有的导频信号均发送频率 f1。以第一个导频信号为例,当接收端对其进行非相干解调后,所计算的频率 f 1上的干扰状态LLR为

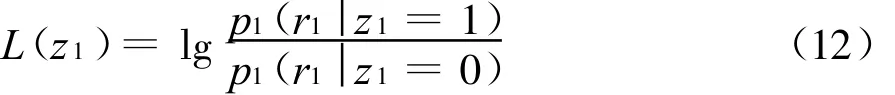
且

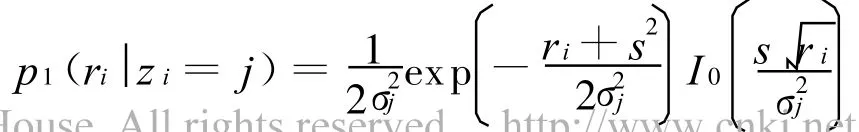
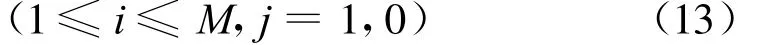
式中:s2=RE b为每跳能量;p 1(ri z i=j)是当发送频率为fi时,所对应的非相干解调输出ri的条件概率密度函数,它是自由度为2的非中心χ2分布。

将式(13)代入式(12)中,便可得

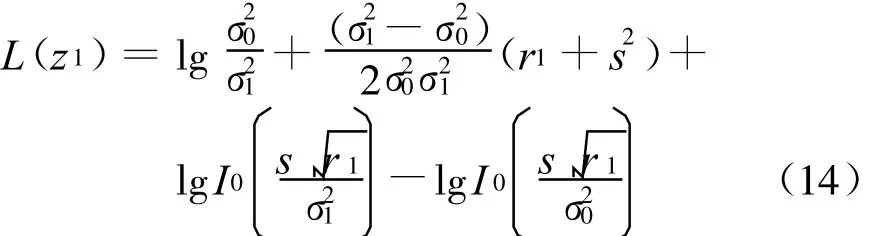
其余频点 fk(2≤k≤M)上的干扰状态LLR可计算为

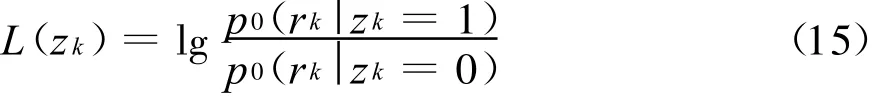
且

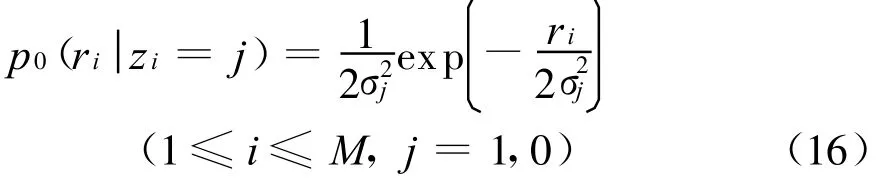
将式(16)代入式(15),则可得

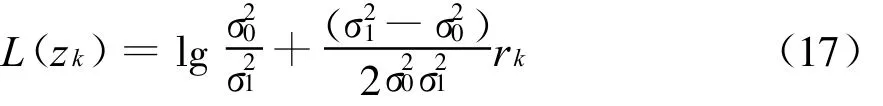
根据式(14)及式(17)得到各频点上的干扰状态初值后,迭代译码器将其作为首次迭代时的干扰状态先验信息,利用该导频信号之后的h跳非相干解调输出r-={r1,r2,…,rh},更新各频点上的干扰状态LLR L(zi r-)为

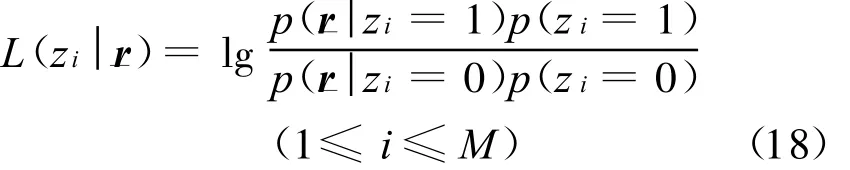
由于所有h跳信号的非相干解调输出均是相互独立的,因此,式(18)可改写为

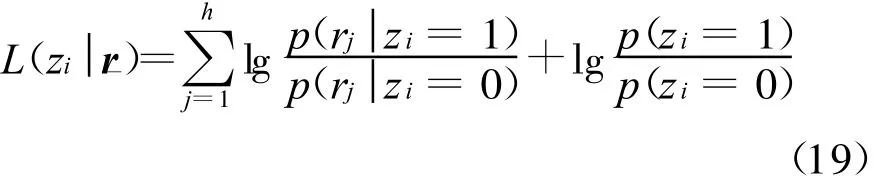
式(19)右边最后一项即为前次迭代所得到的频点f i上的干扰状态先验信息,对于首次迭代,它即是根据导频信号所计算出的干扰状态初值,且

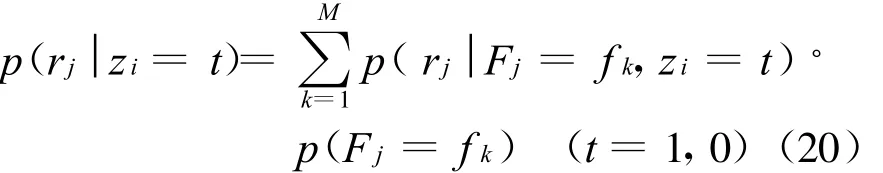
式中:Fj为第j跳的发送频率;p(Fj=fk)为第j跳发送频率f k的概率,它表征差分跳频各跳所发送频点的概率分布,可在迭代译码过程中进行更新,且

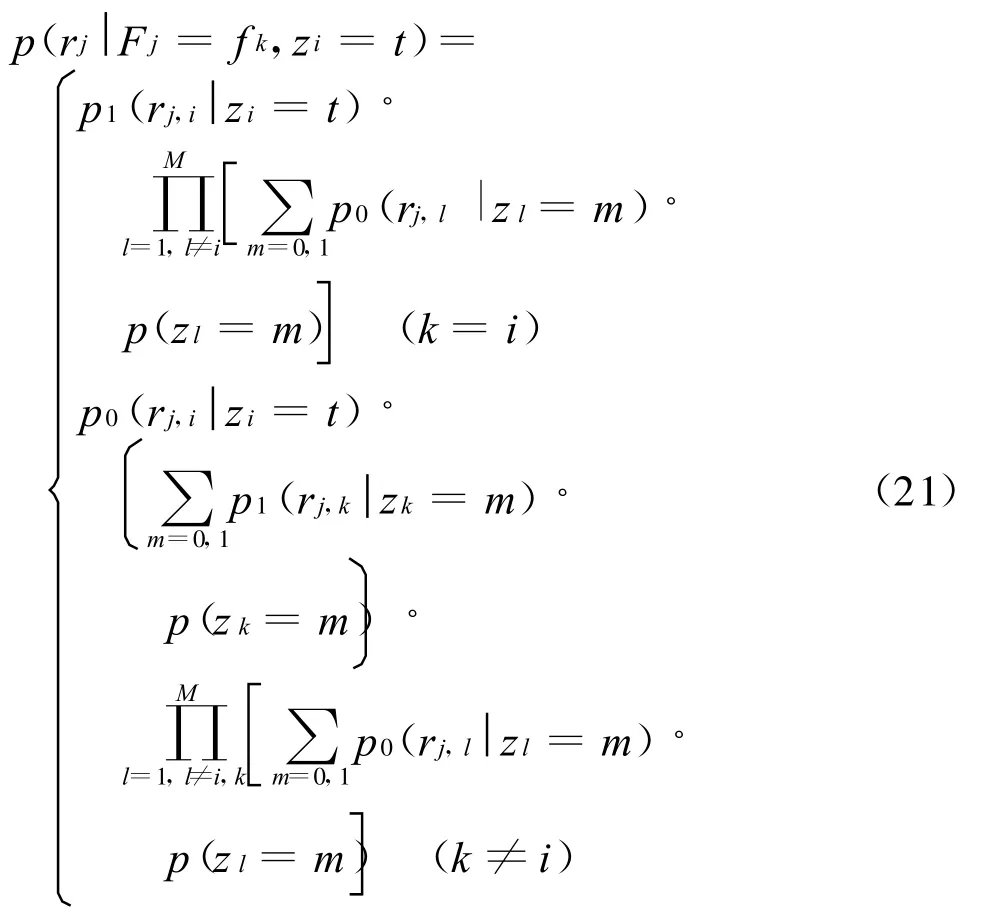
式中,r j,l为第j跳信号非相干解调后对应于频率f l上的输出能量。

显然,若直接计算式(21),其复杂度仍过高。一种简化计算的次优解决方法是根据前次迭代所得到的JSI先验信息,先对频点 fl(1≤l≤M,l≠i)上的干扰状态进行判决,若判决结果zl=1,则在式(21)中,令 p(zl=1)=1,p(z l=0)=0,反之亦然,于是有

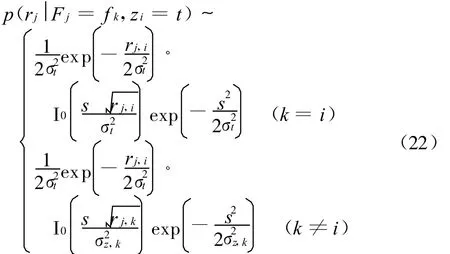
将式(22)代入式(20)及式(19),则可得

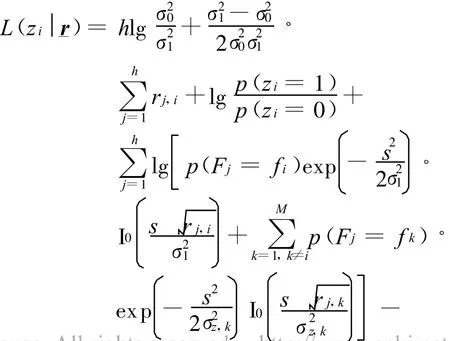
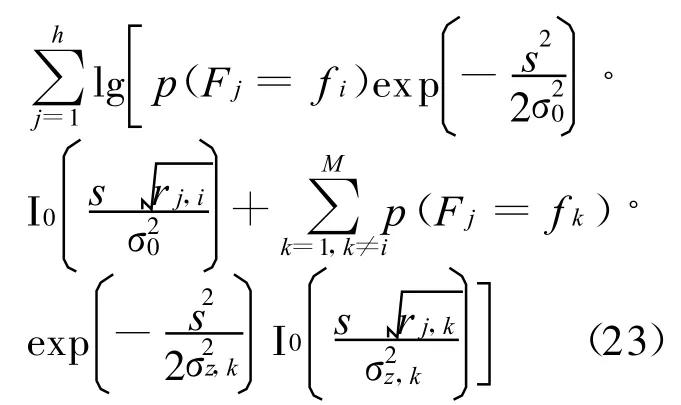
当干扰状态 LLR更新完毕后,SISO译码器便可利用其计算译码时的网格图分支度量,再利用SISO算法进行译码。为了简化计算,仍可由更新后的各干扰状态LLR值先对每个频点上是否存在干扰进行判决,再根据此判决结果计算网格图分支度量。对第 j跳,其分支度量为

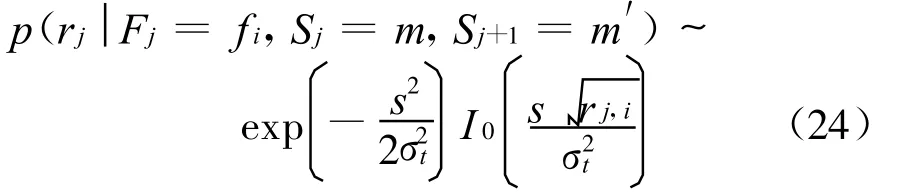
式中:Sj为差分跳频译码器在第j跳时的状态;f i为由状态转移→所确定的发送频率;t=0,1取决于对频点 fi上干扰状态的判决。

5.数值仿真结果与分析

本节给出 LDPC编码差分跳频系统抗部分频带干扰性能的数值与仿真结果。在所有的仿真结果中,LDPC码的码长均为1000,设计码率为0.5,校验矩阵的实现方法参见文献[13]。

在有精确JSI的情况下,优化LDPC码差分跳频系统抗n=8的全频段干扰的BER仿真曲线如图3所示。

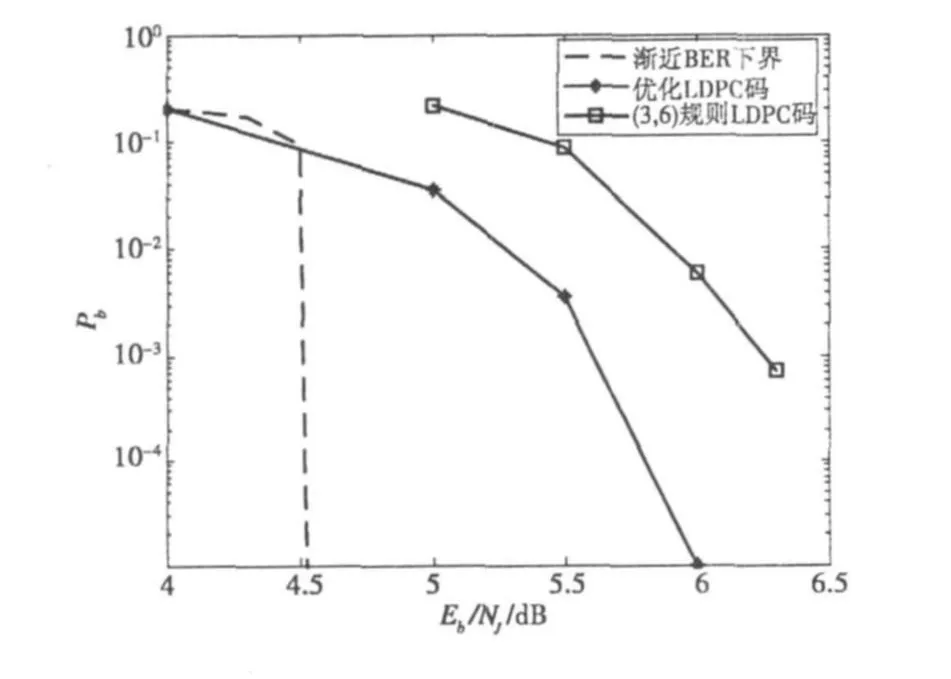
图3 有精确JSI时,LDPC编码差分跳频系统的Pb与Eb/NJ关系曲线

作为比较,还给出了当码长为无限长时,优化LDPC码差分跳频系统的渐近BER下界曲线,以及采用规则LDPC编码的差分跳频BER仿真曲线,其中规则LDPC码的变量节点次数为3,校验节点次数为6。仿真中最大迭代次数设为30。从图3可见,当BER小于10-4时,优化LDPC码相对于规则LDPC码,有0.5～1 d B的信干比改善。而当BER为10-5时,优化LDPC码相对于码长为无限长的理想情况,有1.5 d B的性能差距。

在有精确JSI的情况下,对于不同的干扰频率数,优化LDPC码差分跳频系统为了达到10-3的BER所需的信干比如图4所示,仿真时的最大迭代次数为30。作为比较,还根据无编码系统抗部分频带干扰的BER上界公式[5],给出了无编码系统所需的信干比。从图4可见,采用纠错编码后,最坏情况干扰为n=8的全频段干扰,这表明编码系统具有良好的抗窄带干扰能力。当n=8时,编码系统相对于无编码系统的信干比改善约为2.5 dB,而随着n逐渐减小,信干比改善显著增大,n=5时,信干比改善可达15 dB.

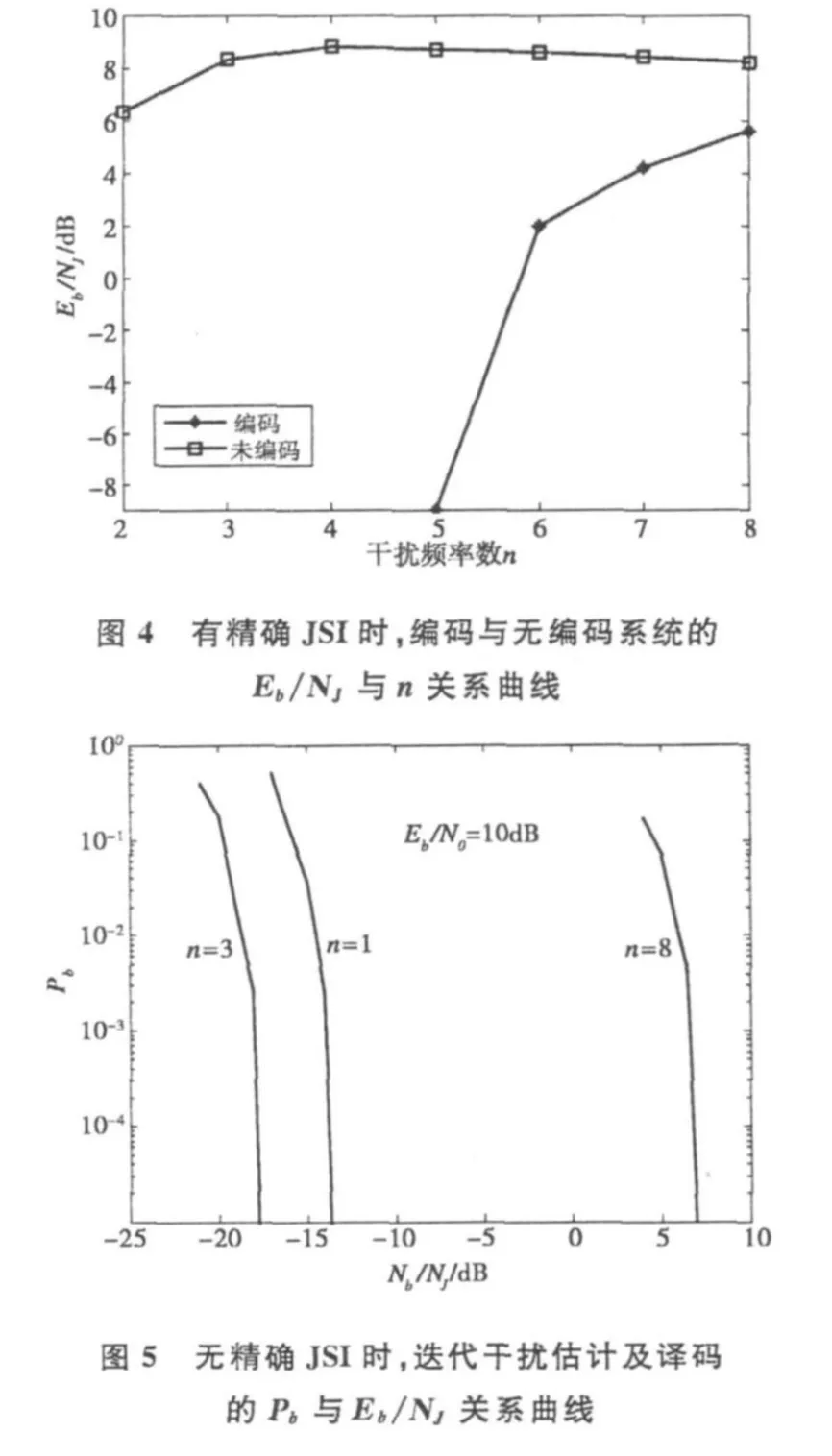
在无精确JSI的情况下,采用迭代干扰状态估计及译码时的仿真曲线如图5所示。信噪比Eb/N0设为10 dB,干扰状态在连续h=20跳内保持不变,仿真时的最大迭代次数为15。从图5可见,最坏情况干扰为n=8的全频段干扰,这表明即使系统不能得到精确的JSI,但利用信道的记忆性,采用迭代干扰状态估计及译码仍可使系统具有良好的抗窄带干扰能力。

6.结 论

在差分跳频抗干扰性能的现有研究成果基础上,将LDPC码引入差分跳频系统,探讨了其对系统抗部分频带干扰性能的改善,得到如下结论:1)在有精确JSI的情况下,编码系统可以显著改善差分跳频的抗窄带干扰能力,这种改善随着干扰频率数的下降而增大,当干扰频率数为5时,信干比改善可达15 d B;2)在无精确JSI的条件下,系统可以采用迭代干扰状态估计及译码算法保持其抗干扰能力,对n=8的系统其最坏情况干扰为全频带干扰,这充分表明了引入LDPC码的优越性。

[1] HERRICK D L,LEE P K.CHESSa new reliable high speed HF radio[C]//MILCOM'96 Conference Proceedings.Washing DC,USA:IEEE,1996:684-690.

[2] HERRICK D L,LEE P K,LEDLOW L L.Correlated frequency hopping-an improved approach to HF spread spectrum[C]//Tactical Communication Conference Proceedings.Fort Wayne,USA:IEEE,1996:319-324.

[3] 陈 智,李少谦,董彬虹.瑞利衰落信道下差分跳频通信系统的性能分析[J].电波科学学报,2007,22(1):126-129.

CHEN Zhi,LI Shaoqian,DONG Binhong.Performance analysis of differential f requency hopping system over Rayleigh fading channels[J].Chinese Journal of Radio Science,2007,22(1):126-129.(in Chinese)

[4] SIMON M K,OMURA J K,SCHOLTZ R A,et al.Spread spectrum communications handbook[M].北京:人民邮电出版社,2002:475-480.

[5] 朱毅超,甘良才,熊俊俏,等.BICM在差分跳频系统中的应用[J].电波科学学报,2009,24(1):15-21.

ZHU Yichao,GAN Liangcai,XIONG Junqiao,et al.Performance of BICM in the differential frequency hopping system[J].Chinese Journal of Radio Science,2009,24(1):15-21.(in Chinese)

[6] 朱毅超,甘良才,熊俊俏,等.短波差分跳频系统抗部分频带干扰性能分析[J].电波科学学报,2006,21(6):885-890.

ZHU Yichao,GAN Liangcai,XIONG Junqiao,et al.Performanceanalysis of shortwave differential frequency hopping systems with partial-band jamming[J].Chinese Journal of Radio Science,2006,21(6):885-890.(in Chinese)

[7] GALLAGER RG.Low-density parity-check codes[M].Cambridge,MA:MIT Press,1963.

[8] MACKAY D.Good error correcting codes based on very sparse matrics[J].IEEE Transactions on Information Theory,2001,47(2):619-637.

[9] BAI Y,LUO W,HAN L.Application of LDPCcodes over GF(q)to DFH communication system[C]//Proceedings of 3rdInternational Conference on Intelligent Information Hiding and Multimedia Signal Processing.Taiwan:IEEE,2007:1-4.

[10]ROBERTSON P,VILLEBRUN E,HOEHER P.A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain[C]//ICC'95 Conference Proceedings.Seattle,USA:IEEE,1995,2:1009-1013.

[11]NARAYANAN K R,STUBER G L.A serial concatenation approach to iterative demodulation and decoding[J].IEEE Transactions on Communications,1999,47(7):956-961.

[12]PROAKS JG.Digital communications[M].4thed.北京:电子工业出版社,2001:304.

[13]RICHARDSON T,SHOKROLLAHI A,URBANKE R.Design of capacity-approaching irregular low-density parity-check codes[J].IEEE Transactions on Information Theory,2001,47(2):619-637.

[14]TEN BRINK S,KRAMER G,ASHIKHMIN A.Design of low-density parity-check codes for modulation and detection[J].IEEE Transactions on Communications,2004,52(4):670-678.

[15]FRANCESCHINI M,FERRARI G,RAHELI R,et al.Serial concatenation of LDPC codes and differential modulations[J].IEEE Journal on selected areas in communications,2005,23(9):1758-1768.

[16]M ILLER G,BURSHTEIN D.Bounds on the maximum-likelihood decoding error probability of low-density parity-check codes[J].IEEE Transactions on Information Theory,2001,47(7):2696-2710.

[17]CHUNG S,RICHARDSON T J,URBANKE R L.A-nalysis of sum-product decoding of low-density paritycheck codes using a Gaussian approximation[J].IEEE Transactions on Information Theory,2001,47(2):657-670.