基于不同天线高度雷达海杂波的蒸发波导反演

张金鹏 吴振森 赵振维 王 波

(1.西安电子科技大学理学院,陕西 西安710071;2.中国电波传播研究所,山东 青岛266107)

1.引 言

蒸发波导是由异常大气折射率环境导致的发生在大面积水体,尤其是海洋上空的一种近永久性电磁波陷获结构,会导致雷达盲区的出现和雷达杂波的增强[1]。蒸发波导的实时精确反演对无线电系统的性能评估,提高雷达的探测性能具有重要的指导与战略意义。

雷达海杂波包含有丰富的近海面大气折射率信息,是一种海洋蒸发波导反演的新途径。国外利用雷达杂波对大气折射率环境的反演研究主要从20世纪90年代末开始的,美国的Wallops'98实验[2]利用S波段空间测距雷达接收了大量海杂波数据,验证了利用雷达杂波反演蒸发波导的可行性,并得到了较好的反演结果。国内近几年已经开展了大气波导的发生机理以及对电磁波传播影响的理论和实验研究[3-6],以及部分大气波导的预报和反演技术研究[7-8],其中对蒸发波导的反演主要基于中性大气层结下Paulus R A的单参数模型[9]。

利用雷达海杂波反演大气波导的技术实质上是一种海杂波的实际测量数据与雷达电波正演传播模拟结果之间相互对比拟合的技术,反演精度受到雷达系统参数、海杂波相关参数,杂波接收环境以及正演和反演的数学模型等多方面因素的影响。其中,描述蒸发波导的修正折射率剖面模型对反演结果至关重要,本文在Paulus R A 单参数模型[9]的基础上,引入蒸发波导强度,建立了两参数蒸发波导修正折射率剖面模型,该模型可以更好的描述实测剖面。利用此模型,考虑不同天线高度的海杂波含有不同的波导特征信息,可能会提高波导剖面参数的反演精度,建立了基于可调天线高度雷达系统的蒸发波导反演模型。

2.雷达海杂波反演蒸发波导的影响因素

影响雷达海杂波反演蒸发波导精度的因素主要有:1)雷达电波正向传播模拟计算的准确性(正演问题);2)蒸发波导剖面模型的合适性;3)雷达系统参数的选取;4)海杂波相关参数;5)反演优化算法的性能(反演问题)。

影响因素4)中涉及的海杂波相关参数主要有海面粗糙度、风速、杂波测量噪声和统计分布类型等,这些参数会影响实测雷达海杂波的功率—距离分布,改变波导反演算法的输入信息,进而影响波导剖面的反演结果,文献[10]已对该影响因素进行了详细的分析。反演优化算法的性能(影响因素5))对蒸发波导的反演精度、稳定性以及收敛速度也有重要的影响,但属于数学问题,本文暂不讨论。本文主要对影响因素1)～3)进行讨论与分析。

2.1 雷达海杂波功率的正演计算

反演问题是基于正演问题进行的。利用雷达海杂波进行蒸发波导反演要基于雷达电波的正向传播模拟计算,雷达杂波功率的计算精度是影响波导剖面反演的首要因素。

在一定的大气环境下,不考虑接收机噪声时雷达接收到的海杂波功率[11]可以表示为

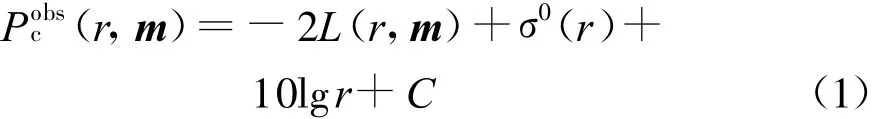
式中:m代表随距离和高度变化的修正折射率剖面,本文中假设m为水平均匀的;L(r,m)为雷达波到达距离r(km)处的单程路径损耗;σ0(r)是距离发射源r(km)处的海面后向散射系数;C为与雷达发射功率Pt、增益 Gt、Gr等有关的常数,经过简化变型后的计算公式为

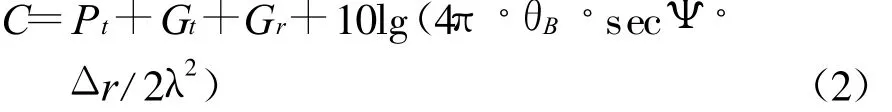
式中:θB为雷达天线方位向波瓣宽度(rad);Ψ为掠射角(rad);Δr为雷达距离分辨率(m)。式(1)和(2)中参量 Pobsc,L,σ0,C,Pt,Gt,Gr的单位取dB.

海杂波功率式(1)的计算关键是路径损耗L的计算,指的是发射系统的等效全向辐射功率(EIRP)与接收系统各向同性接收天线所接收到的可用功率之比,与收、发天线的方向性无关。大气波导环境下的电波单程路径损耗可表示为

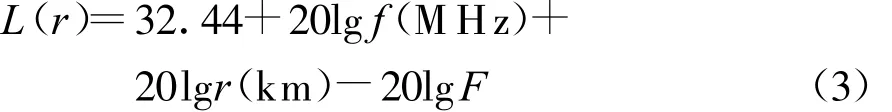
式中:r为空间某点到发射源的距离;F为传播因子,定义为F=|E/E0|,E、E0分别为接收点和自由空间接收点场强。传播因子使用抛物方程(PE)的离散混合傅立叶解法(DMFT)计算[12]。

2.2 两参数蒸发波导M剖面建模

基于雷达海杂波的对流层波导反演都基于参数化的大气折射率剖面模型,模型的优劣严重影响波导剖面的反演精度。对蒸发波导反演而言,不同的大气稳定度条件下,波导剖面的形式是不同的,我们通常使用的是热中性大气条件下Paulus R A[9]给出的单参数对数线性模型

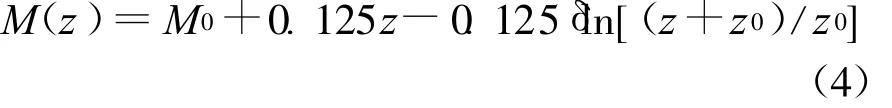
式中:δ为蒸发波导高度(m);z0为空气动力学粗糙度因子,取z0=1.5×10-4m;M0为海面高度处的大气修正折射率。

Paulus R A的单参数模型在大部分情况下能有效描述近海面蒸发波导剖面,但存在如下缺点:

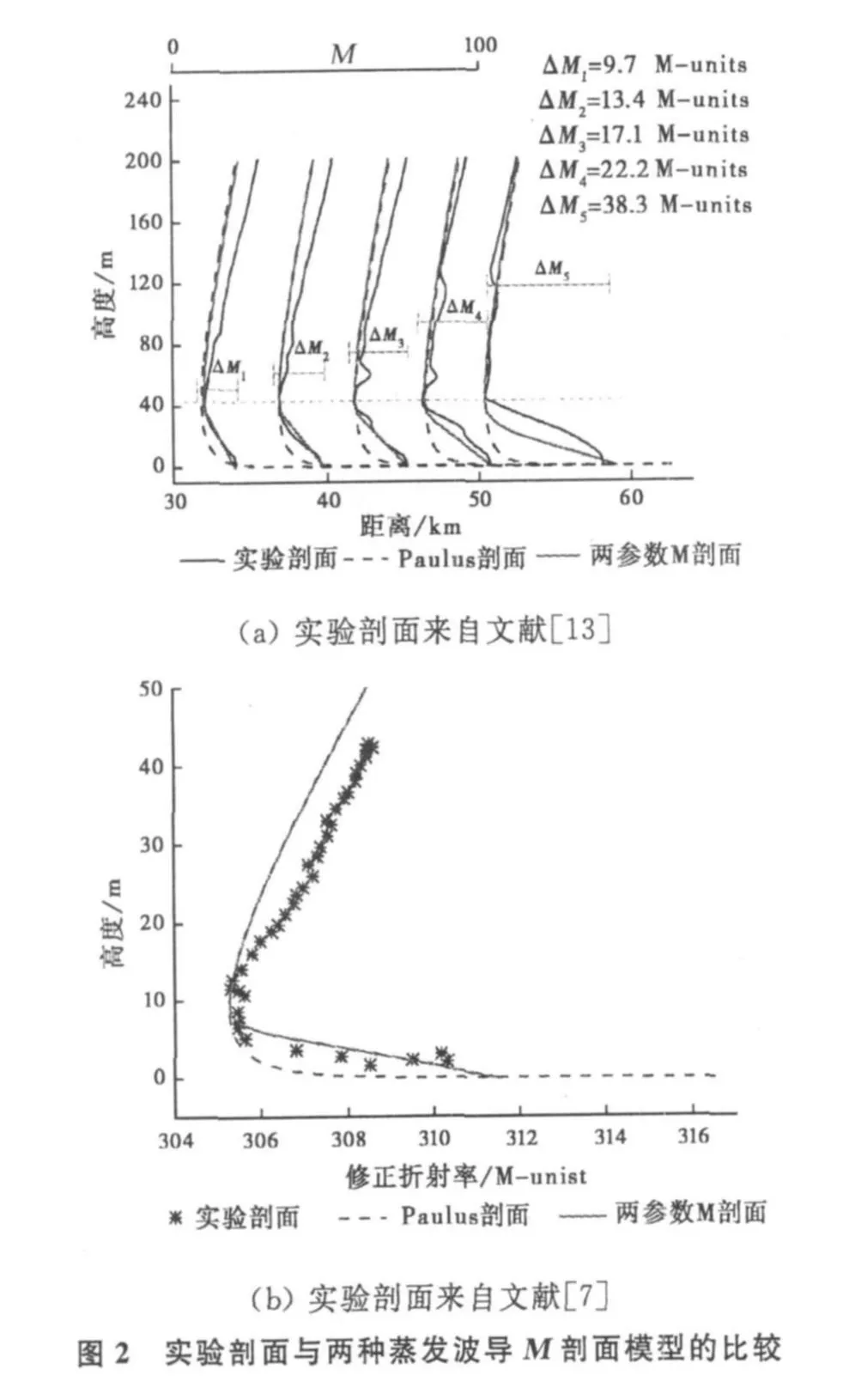
1)大气的修正折射率结构仅由波导高度来描述,这在实际中是有局限性的,还应体现波导陷获层顶与海面处的修正折射率之差带来的影响,我们定义其为波导强度ΔM.波导高度与强度在很多情况下并不一一对应,如文献[13]图4。另外,Douvenot R等人[14]也指出仅用波导高度一个参数进行蒸发波导M剖面建模具有局限性。

2)蒸发波导高度δ处M剖面斜率的变化率(二阶导数)唯一地由波导高度确定,不能描述波导高度处修正折射率的斜率变化较快的情况,如图2(a)。

3)该剖面模型在高度接近0时有很长的拖尾,修正折射率梯度异常大,从而使得水平方向的电磁波产生大角度的折射,阻止了长距离的传播,式(4)所示模型中的对数规律在非常低的高度时并不适用[15]。另外,经过基于2.1节的雷达海杂波功率的计算可以验证,蒸发波导折射率剖面拖尾的长短只影响海杂波接收功率的幅度,对杂波功率的距离向梯度影响很小,因此,对基于雷达海杂波的蒸发波导折射率剖面反演而言,反演剖面的拖尾经过加长或缩短以后都可以认为是正确反演出的剖面,即一组海杂波数据可对应不同长短拖尾的折射率剖面,这说明长拖尾剖面是不适用于波导反演的。

基于中性大气层结下,Paulus R A给出的单参数剖面模型,建立了如图1所示的蒸发波导的两参数修正折射率剖面。

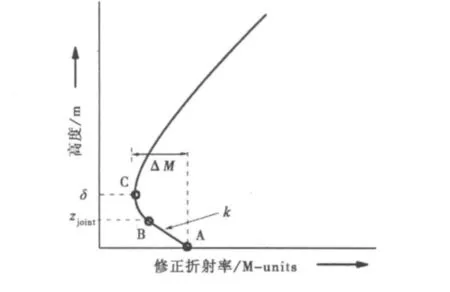
图1 两参数蒸发波导垂直修正折射率剖面

式(4)所示剖面的修正折射率高度向梯度的变化率为

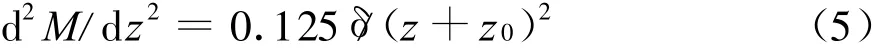
为使该变化率可以调节,引入调节因子 ρ(ρ＞0),则相应的M剖面变为

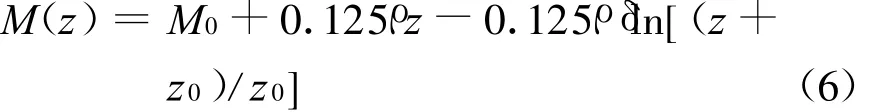
为保证蒸发波导高度δ以上的剖面不变,式(6)只用于描述小于波导高度的M剖面。

图1中AB为替换式(6)所示模型中对数剖面的直线段(高度小于δ),关于高度的斜率记为k(k≤0)。式(6)所示修正折射率M随高度的变化率为

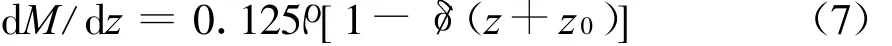
为使直线段AB的斜率与接合点B处式(6)所示M剖面的斜率相等,实现光滑接合,令式(7)等于直线段 AB斜率k,可得

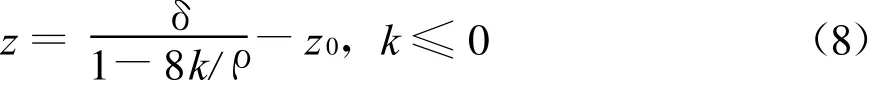
以此高度作为剖面接合点高度可使得整个剖面的修正折射率高度向梯度连续,记此接合点高度为z joint,如图1中B点。

z≤z joint时的蒸发波导剖面(图1中直线段 AB)为

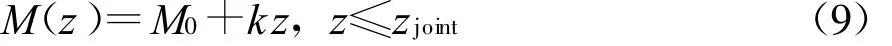
为使得式(6)所示M剖面与式(9)所示直线段剖面AB在zjoint处的M值相同,在式(6)剖面中引入修正折射率补偿项Moffset1 如下

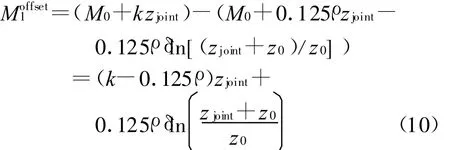
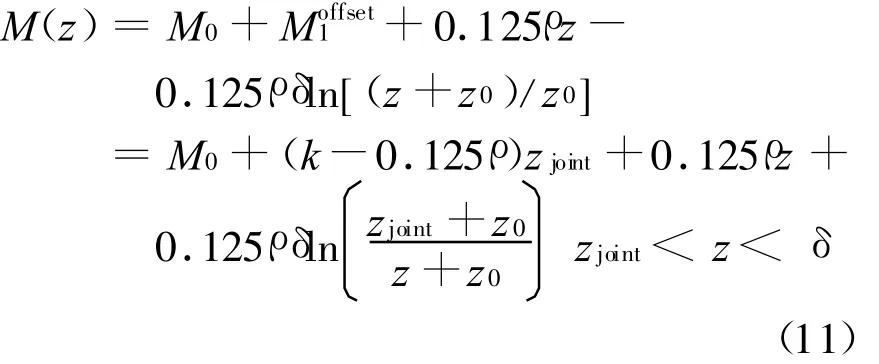
高度大于波导高度δ的剖面使用Paulus R A的单参数模型式(4),为使得该剖面与式(11)所示剖面BC在蒸发波导高度δ处的M值相同,在式(4)剖面中引入补偿项Moffset2如下

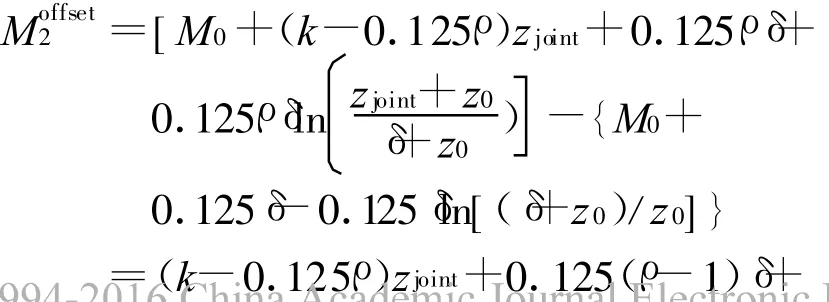
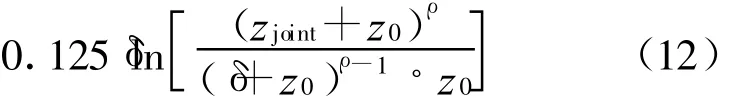
z≥δ时的蒸发波导剖面为

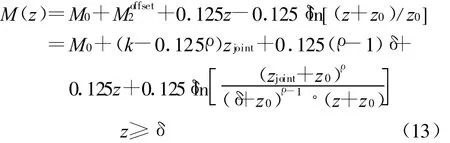
式(9)、(11)、(13)组成的新蒸发波导剖面的波导强度ΔM为

则称算法A满足ε-差分隐私.其中，Pr[.]表示隐私被披露的概率，它是由算法A的随机性所控制(与攻击者的背景知识无关)；ε是隐私保护参数，表示隐私保护的力度，ε越小意味着隐私保护力度越强.定义3本质上刻画了基于随机算法A输出的两个相邻矩阵的不可分程度.

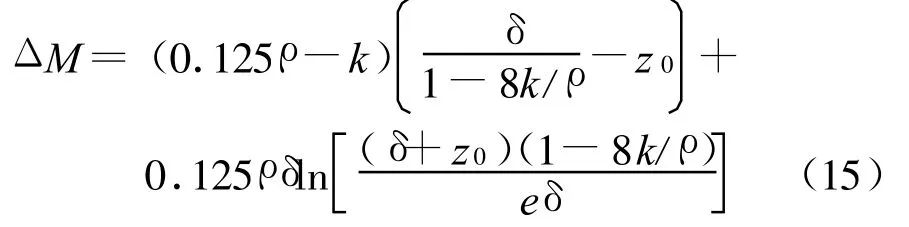
此即用直线段AB的斜率k表征蒸发波导强度ΔM的关系式。

式(8)、(9)、(11)、(13)、(15)即为蒸发波导两参数修正折射率剖面模型,该模型由蒸发波导高度δ与波导强度ΔM两参数决定,在一个参数固定时另一参数可以自由变化,更加灵活地描述实际蒸发波导剖面。

为了验证本文给出的蒸发波导两参数修正折射率剖面模型的适用性,图2给出了两组实验剖面与Paulus R A的单参数模型和本文的两参数模型的比较,其中图2(a)中的实测剖面波导高度较大,可以看为特殊情况下的蒸发波导M剖面。通过波导高度与波导强度的调节,可以看出,本文的两参数M剖面模型与实验剖面吻合的更好,避免了单参数模型中δ高度处修正折射率的斜率变化较慢和近海面的长拖尾现象。另外,图2(a)中不同距离处的剖面具有基本相同的波导高度,但波导强度不同,本文的两参数剖面模型可以通过调节波导强度 ΔM而达到与每一距离处剖面的较好吻合,而Paulus R A单参数剖面在波导高度δ确定后,波导强度ΔM也相应的唯一确定,影响了与不同剖面的吻合。

2.3 雷达系统参数对蒸发波导反演的影响

由于基于雷达系统的大气低空折射率剖面反演使用的是雷达杂波功率—距离信息,因此,影响海杂波功率—距离分布信息的所有雷达系统参数都影响海洋蒸发波导的反演,如雷达功率、增益、频率、天线高度、距离分辨单元以及极化方式。增大雷达发射功率与增益可以提高雷达接收到海杂波的杂噪比(CNR),从而减少噪声的影响,提高波导反演的精度。雷达距离分辨单元的大小以及极化方式尽管也影响波导的反演,但直接影响的是海杂波的统计分布[16],属于影响因素4),详细描述见文献[10]。本文主要研究雷达频率和天线高度对蒸发波导反演的影响。

2.3.1 雷达频率的影响

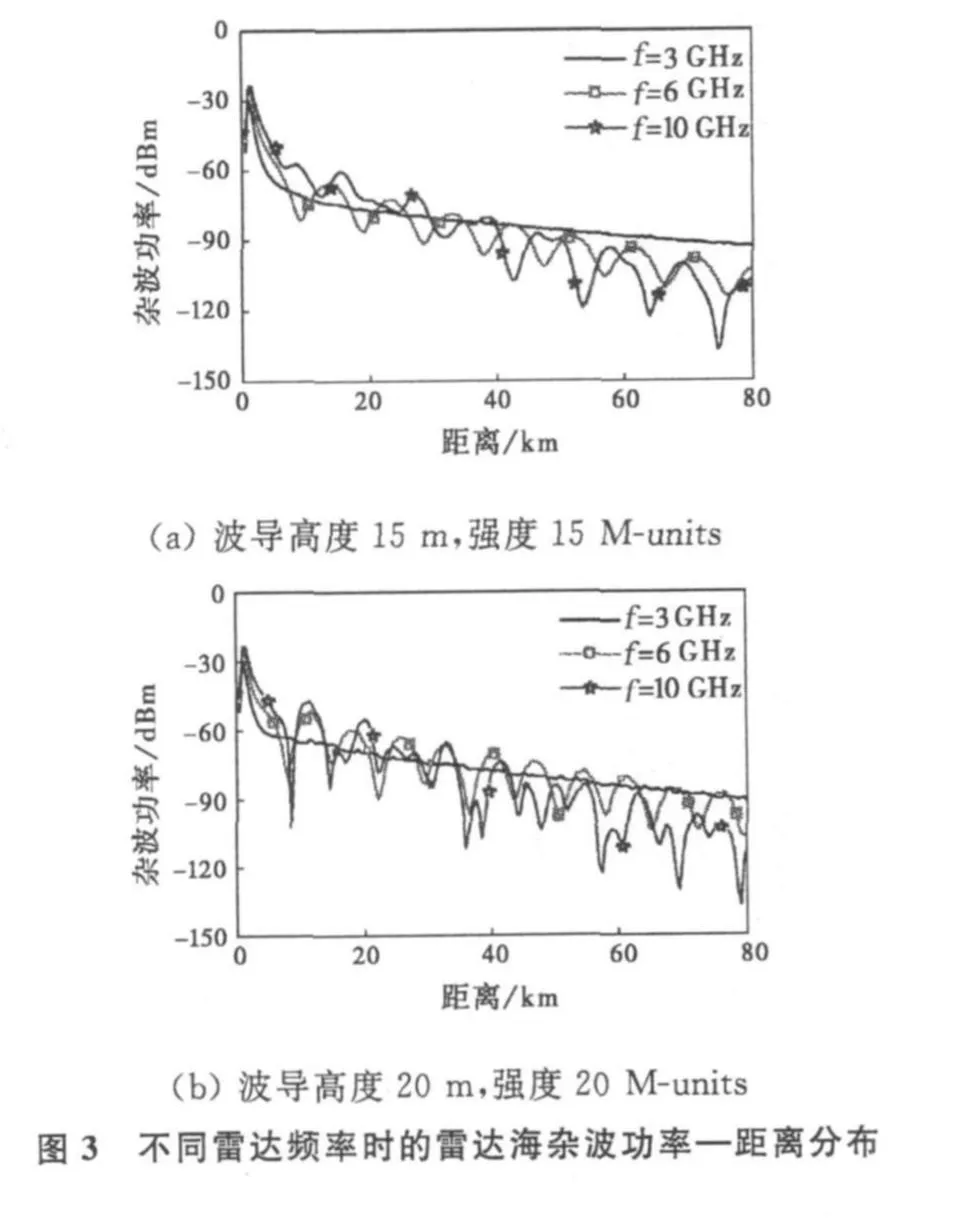
类似于金属波导内传播的电磁波,蒸发波导内的雷达电波频率不同,波导模模式和数量不同,雷达接收到的海杂波信号距离衰减速度及多模干涉现象也会不同。因此,不同频率雷达接收到的携带不同信息的海杂波将严重影响蒸发波导的反演质量。

图3给出了两组蒸发波导剖面参数,天线高度为8 m时,不同雷达频率对应的海杂波功率,使用的雷达系统参数如表1所示,除杂噪比、天线高度与仰角为假设外,其他参数均来自一次蒸发波导对舰载雷达探测性能的影响验证实验[17]。雷达接收到的海杂波源于海面有效散射高度处的电磁散射,有效散射高度h e≈0.6h a,h a为平均海浪高度。假设海情为4级,对应的平均浪高h a=0.945 m,则海面有效散射高度h e≈0.57 m.从图3可以看出,发射频率不同时,雷达接收到的海杂波功率幅度和距离向梯度有明显不同,功率曲线随距离的上下振荡程度也不同,这是由于波导模之间的干涉造成的,频率越高,波导模之间的干涉效应越明显。这种由于雷达频率不同而给海杂波功率—距离分布带来的差异将影响蒸发波导的反演。

2.3.2 天线高度的影响

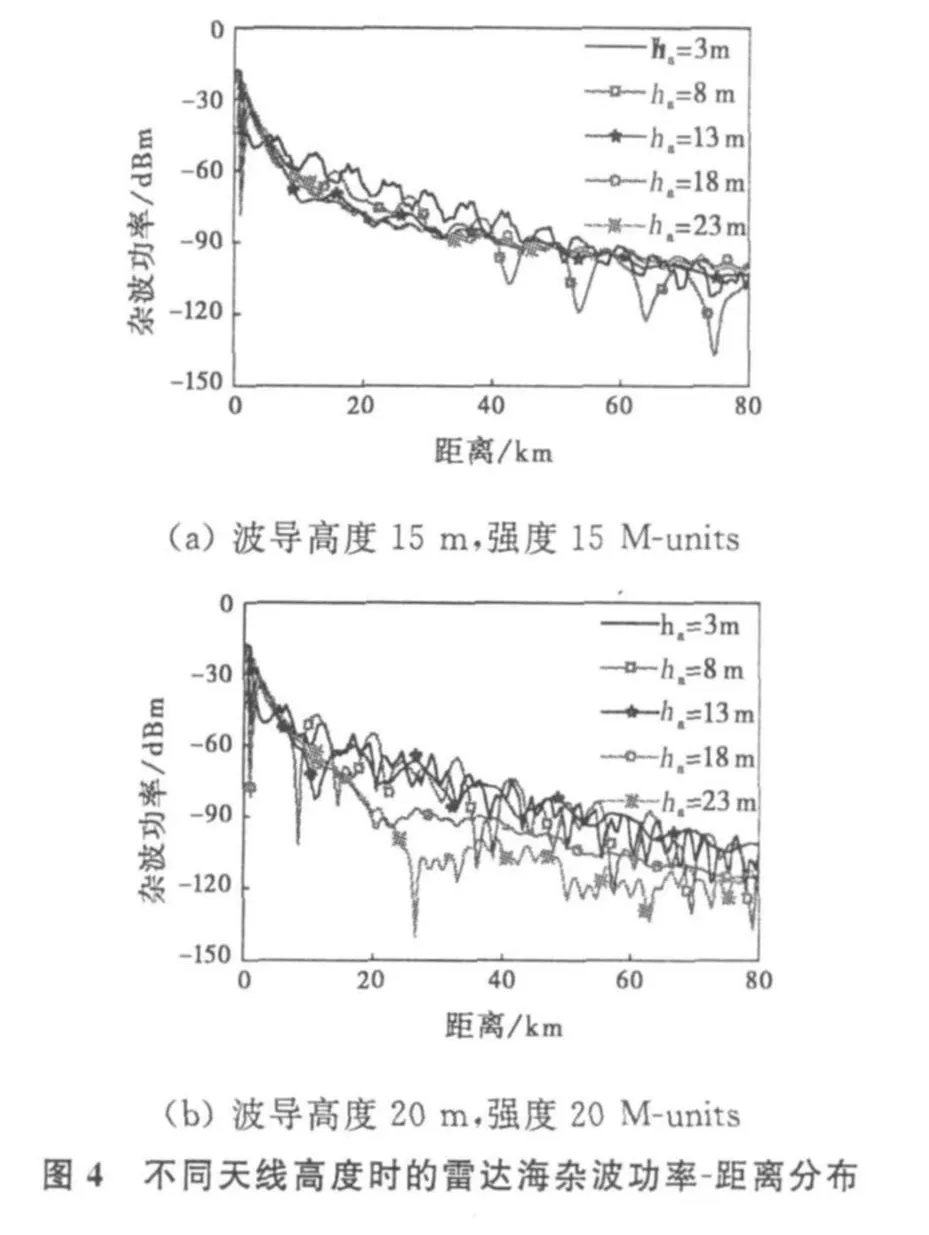
在利用雷达系统进行海洋蒸发波导探测反演中,雷达天线作为电磁波发射源,它在蒸发波导陷获层中的相对位置直接决定电磁波的陷获程度和海杂波接收功率的携带信息,影响实测和正演模拟杂波功率的距离分布,进而影响蒸发波导剖面的反演。

图4给出了雷达频率为10 GHz,5个天线高度下雷达接收到的海杂波功率随距离的变化,雷达系统参数如表1。对应两组蒸发波导高度与强度,发射天线各有位于波导陷获层之内与之外的情况。可以看出,天线架设高度不同时,雷达接收到的海杂波功率幅度和多模干涉效应都有明显的变化,波导越强(图4(b)),变化越明显。这说明不同的天线高度会获得含有不同波导特征信息的海杂波,得到波导参数不同的反演精度。这种差异给雷达杂波反演蒸发波导中天线的架设高度提出了要求。

3.提高蒸发波导反演精度的方法

利用雷达杂波反演大气波导的基础是获得某大气环境下的杂波特征信息。为了达到较高的反演精度,就需要尽可能多的获得杂波信息来作为反演算法的输入。通过2.3节中天线高度对海杂波接收功率的影响分析可知,天线架设高度不同,雷达接收到的海杂波信息就明显不同,采用多个天线高度的丰富海杂波信息必然会提高波导参数的反演精度。在实际应用中,天线高度可以通过天线的伺服系统进行调节,简单易行,采用单部雷达便可获得用于波导反演的大量海杂波信息,而不必采用多部雷达接收机。

本文基于天线高度可调的雷达接收机,建立了如下的两参数蒸发波导M剖面反演模型:

1)利用天线伺服系统调节天线,接收多个天线高度h1,h2,…,hn时的实测海杂波功率。对实测雷达海杂波功率数据进行中值滤波处理,去除杂波尖峰信号。将滤波后的杂波功率在距离r1、r2、…rN处进行离散(此离散距离即为波导传播正演计算的不同步进),得到目标功率向量Pobs1,Pobs2,…,Pobs3以此n个向量作为反演算法的输入。

2)两参数蒸发波导M剖面建模。修正折射率空间结构建模即为确定折射率参数维数,构建修正折射率与空间位置对应关系的过程。实际环境中M随传播距离而变化,但通常认为这种水平变化是缓慢的,因此本文假定M为水平均匀的,垂直M剖面采用2.2节给出的两参数蒸发波导模型。

3)正演模拟天线高度分别为h1,h2,…,hn时的雷达海杂波功率Pci(i=1,2,…,n)。

4)建立自适应目标函数。反演过程中目标函数用来估计正演模拟的杂波功率与实测功率的吻合程度,选择合适的目标函数进行优化搜索对反演结果具有重要的影响。对基于可调天线高度雷达系统的波导参数反演而言,最优剖面应该使得每一天线高度的正演模拟杂波功率Pci(i=1,2,…,n)与相应的实测功率Pobsi(i=1,2,…,n)吻合的最好,因此属于多目标优化的问题。

收距离r较大处的海杂波信号CNR相对较大,会给反演结果带来消极的影响,因此,为了减小远距离处杂波信息对目标函数的贡献,我们使用如下的含线性距离权重的最小二乘目标函数

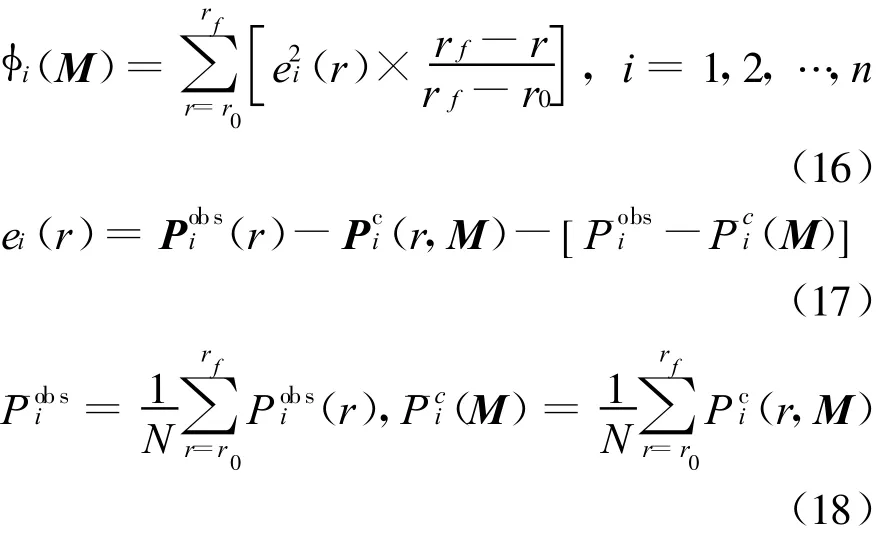
式中:M为蒸发波导剖面参数矢量;r0和rf为用于反演的杂波功率起始距离与终止距离;N为距离步个数。

对基于可调天线高度雷达系统的波导参数反演而言,需要使得对应每一天线高度的目标函数φi(M),i=1,2,…,n都达到最优值,我们采用处理多目标优化问题中最常用的统一目标法,将各目标函数进行加权组合,引入如下的自适应目标函数

式中,ωi为对应天线高度hi时的分目标函数φi(M)的加权因子,取决于不同天线高度时雷达杂波携带波导特征信息的相对丰富程度,且由2.3节中天线高度对海杂波功率的影响分析可知,天线高度不同,则波导模干涉状态就不同,但目前无法定量地说明哪个天线高度携带的波导特征信息更加丰富,因此我们采用等比例加权因子

5)利用优化算法对自适应目标函数 Φ(M)进行优化,对应目标函数最小的蒸发波导剖面即为最佳反演剖面。

4.反演结果与讨论

为了验证第3节中的提高蒸发波导反演精度的方法,利用可调天线高度雷达接收到的3个天线高度的海杂波数据作为伪实测数据,进行了蒸发波导高度与强度两参数的反演分析,并与固定天线高度的反演进行了比较。雷达工作频率采用10 GHz,其他所有雷达系统参数如表1所示。

自适应目标函数使用粒子群算法(PSO)[19]进行优化,根据雷达杂波反演蒸发波导的实际情况,初始参数设置为:种群规模50,进化代数10代,波导高度与强度搜索范围分别为0～35 m和0～40 M-units,对应于波导高度与强度的粒子飞行速度最大值分别为3.0 m和4.0 M-units.

为了使正演模拟的伪实测雷达杂波功率更接近于实测数据,本文加入了定量的高斯白噪声。噪声水平的量化使用初始反演距离r0处的CNR来表示,它与海面散射系数(NRCS)σ0的关系为

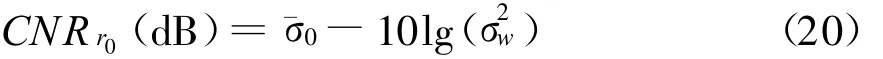
式中:¯σ0代表海面散射系数的均值(d B);σ2w为噪声方差。本文中波导反演使用的杂波功率最大接收距离为r f=80 km,最小接收距离r0和此距离处的杂噪比按文献[8]设定为10 km和40 d B.图5中粗糙曲线为加入CNRr0=10 km=40 dB的高斯噪声后的伪实测雷达海杂波功率,蒸发波导高度与强度组合为(20 m,15 M-units)。

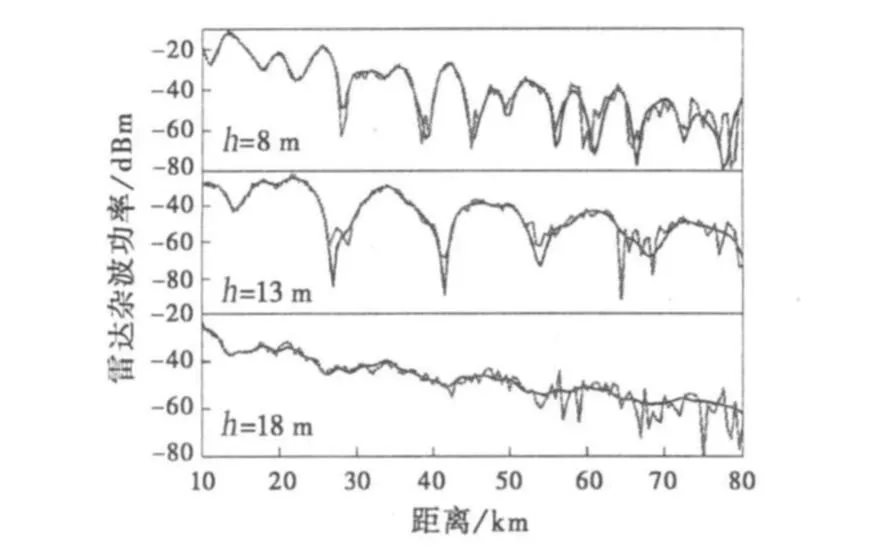
图5 伪实测雷达海杂波功率示意图

以9种代表性蒸发波导高度与强度组合为例,表2给出了基于可调天线高度雷达接收机的4种反演方法的200次蒙特卡罗反演统计结果。4种反演方法采用的雷达杂波数据分别来自(a)天线高度8 m,(b)天线高度13 m,(c)天线高度18 m,(d)天线高度可调(8 m+13 m+18 m)。从表2可以看出,除蒸发波导参数为(20 m,20 M-units)时,可调天线高度比天线13 m时的反演结果稍差外,其他情况下利用可调天线高度的雷达海杂波反演的波导参数均方根误差明显比固定天线高度时小,反演精度更高。为了更加直观的看到4种方法的反演结果,图6给出了其中一组蒸发波导参数(20 m,15 M-units)时相应的200次反演结果的空间分布与概率分布情况。从图6可以看出:

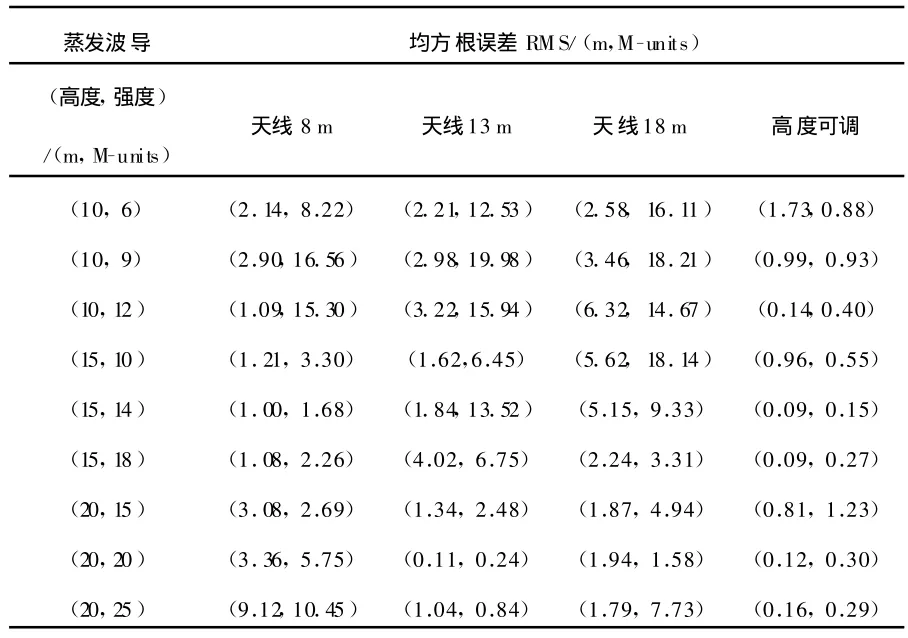
表2 基于可调天线高度雷达接收机的蒸发波导反演统计结果

1)采用不同天线高度接收的雷达杂波反演的蒸发波导参数分布明显不同,说明雷达天线高度的选取对波导反演具有重要的影响。

2)3个天线高度时的反演结果皆分布不够集中,存在许多不同的反演失败点,说明各分目标函数都存在局部极值且极值特性不同。

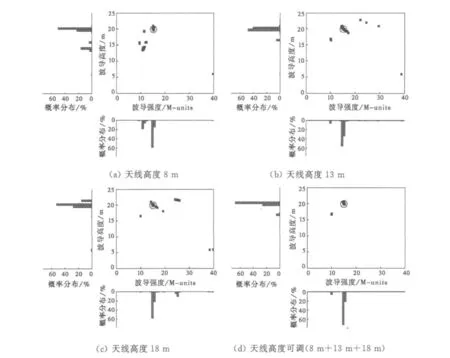
图6 基于可调天线高度雷达接收机的蒸发波导(20 m,15 M-units)反演结果分布

3)基于可调天线高度雷达杂波的反演中,由于使用了具有不同局部极值特性的分目标函数组成的自适应目标函数,反演结果分布更加集中,成功率更高,说明了本文基于天线高度动态可调雷达系统的海洋蒸发波导反演模型具有较高的反演精度。

5.结 论

讨论了利用雷达海杂波进行近海面蒸发波导监测与反演的关键影响因素,根据实际情况中蒸发波导高度与强度并不严格一一对应的情况,建立了两参数蒸发波导剖面,并在此基础上提出了提高海洋蒸发波导参数反演精度的方法。本文反演结果表明:基于可调天线高度雷达系统的反演结果分布集中,稳定性高,有效克服了固定天线高度反演中存在大量局部极值点的情况,提高了海洋蒸发波导的反演精度。实际海洋环境中的大气波导表现为修正折射率剖面距离向与方位向非均匀的情况,基于多雷达台站进行非均匀大气波导的区域反演研究具有极高的应用价值。

[1] 张 瑜,吴少华.大气波导传播类型及特性分析[J].电波科学学报,2009,24(1):185-191.

ZHANG Yu,WU Shaohua.Analysis of the types and characteristics of atmospheric duct propagation[J].Chinese Journal of Radio Science,2009,24(1):185-191.(in Chinese)

[2] ROGERS L T,HATTAN C P and STAPLETON J K.Estimating evaporation duct heights from radar sea echo[J].Radio Science,2000,35(4):955-966.

[3] 姚展予,赵柏林,李万彪,等.大气波导特征分析及其对电磁波传播的影响[J].气象学报,2000,58(5):605-616.

YAO Zhanyu,ZHAO Bolin,LI Wanbiao,et al.The analysis on characteristics of atmospheric duct and its effects on the propagation of electromagnetic wave[J].Acta Meteorologica Sinica,2000,58(5):605-616.(in Chinese)

[4] 孙 方,王红光,康士峰,等.大气波导环境下的射线追踪算法[J].电波科学学报,2008,23(1):179-194.

SUN Fang,WANG Hongguang,KANG Shifeng,et al.A ray tracing algorithm for duct environment[J].Chinese Journal of Radio Science,2008,23(1):179-194.(in Chinese)

[5] 焦 林,张永刚.大气波导条件下雷达电磁盲区的预报研究[J].西安电子科技大学学报(自然科学版),2007,34(6):989-994.

JIAO Lin,ZHANG Yonggang.Prediction of theelectromagnetic shadow zone under the atmospheric duct[J].Journal of Xidian University,2007,34(6):989-994.(in Chinese)

[6] 刘爱国,察 豪.海上蒸发波导条件下电磁波传播损耗实验研究[J].电波科学学报,2008,23(6):1199-1203.

LIU Aiguo,CHA Hao.Experiment study of electromagnetic wave propagation loss in oceanic evaporaiton duct[J].Chinese Journal of Radio Science,2008,23(6):1199-1203.(in Chinese)

[7] 王向敏.海上大气波导的预测方法[D].南京:南京信息工程大学遥感学院,2007.

WANG Xiangmin.A study on the atmospheric duct over ocean and its prediction[D].Nanjing:Nanjing U-niversity of Information Science and Technology,School of Remote Sensing,2007.(in Chinese)

[8] 盛 峥,黄思训,赵小峰.雷达回波资料反演海洋波导中观测值权重的确定[J].物理学报,2009,58(9):6627-6632.

SHENG Zheng,HUANG Sixun,ZHAO Xiaofeng.The determination of observation weight in inversion ocean duct using radar clutter[J].Acta Physica Sinica,2009,58(9):6627-6632.(in Chinese)

[9] PAULUS R A.Evaporation duct effects on sea clutter[J].IEEE Transactions on Antennas and Propagation,1990,38(11):1765-1771.

[10] YARDIM C,GERSTOFT P,and HODGKISS W S.Sensitivity analysis and performance estimation of refractivity from clutter techniques[J].Radio Science,2009,44(RS1008).

[11] GERSTOFT P,ROGERS L T,KROLIK J L,et al.Inversion for refractivity parameters from radar sea clutter[J].Radio Science,2003,38(3):8053.

[12] DOCKERY G D,KUTTLER J R.An improved impedance-boundary algorithm for fourier split-step solutions of the parabolic wave equation[J].IEEE Transactions on Antennas and Propagation,1996,44(12):1592-1599.

[13] GERSTOFT P,HODGKISSW S,ROGERSL T,et al.Probability distribution of low altitude propagation loss from radar sea clutter data[J].Radio Science,2004,39(RS6006).

[14] DOUVENOT R,FABBRO V,BOURLIER C,et al.Retrieve the evaporation duct height by leastsquares support vector machine algorithm[J].Journal of Applied Remote Sensing,2009,3(033503):1-15.

[15] IVANOV V K,SHALYAPIN V N and LEVADNY Y V.Microwave scattering by tropospheric fluctuations in an evaporation duct[J].Radiophysics and Quantum Electronics,2009,52(4):277-286.

[16] LONG M W.Radar Reflectivity of Land and Sea[M].3rd ed.London:Artech House,2001.

[17] ANDERSON K D.Radar measurements at 16.5 GHz in the oceanic evaporation duct[J].IEEE Transactions on Antennas and Propagation,1989,37(1):100-106.

[18] CLERC M.Particle Swarm Optimization[M].London:ISTE Publishing Company,2006.