SOCP宽带波束形成器非样本频点上恒定束宽问题研究

杨 君 漆 峰

(1.装备学院 北京 101416;2.63812部队 海南 571339)

0 引言

宽带波束形成是实现频域宽开的关键技术，是数字阵列雷达(DAR)适应复杂电磁环境的必然选择［1］。宽带波束形成研究主要集中在束宽的频率稳定性方面，目前主要有基于DFT变换的频域实现方法和基于FIR滤波器的时域实现方法［2］，其中前者虽然可以利用FFT快速运算结构减少计算量，但是存在子带分割误差以及FFT滤波误差［3］，使得波束形成输出相对于源信号存在失真［2］，该方法主要用于要求算法快速低功耗的侦察雷达上;基于FIR滤波器的时域实现方法是直接对整个频带进行波束形成，不存在上述频域方法的问题，是宽带波束形成的理想方法，这种波束形成器设计的主要工作就是设计阵元FIR滤波器，每个阵元FIR滤波器的相同频点上的频率响应组成该频点上波束形成器，而其设计的核心原则就是尽可能的保持带内各个频点上的波束形成器的束宽相同，即所谓的恒定束宽问题。阵元FIR滤波器设计是一个多参数优化问题，目前常用的方法就是将滤波器设计问题等价转换成二阶锥 规 划［4-6］(Second-order Cone Programming，SOCP)问题，然后使用 MATLAB 的 Sedumi函数［7］进行优化设计。虽然SOCP可以在波束形成器的主瓣宽度、旁瓣级、主瓣响应误差、稳健性等多个指标之间进行全面的折中处理，但是其优化的对象只能是目标频带内有限个离散的样本频点，而对那些非样本频点上的波束响应却无任何约束，如果非样本频点上的束宽频率稳定很差的话，这个宽带波束形成的效果必然大大受到影响，本文正是围绕非样本频点上的束宽频率稳定性问题展开研究。

1 非样本点束宽频率稳定性分析

所谓束宽的频率稳定性是指宽带波束形成器的波束宽度在带宽内随频率变化的情况，束宽在各频点上的变化越小频率稳定性越好，使束宽方向内入射的信号频谱产生的畸变越小。本文用各频点上3dB束宽的方差来恒量波束形成器在该族频点上的束宽稳定性。3dB束宽的方差定义为:

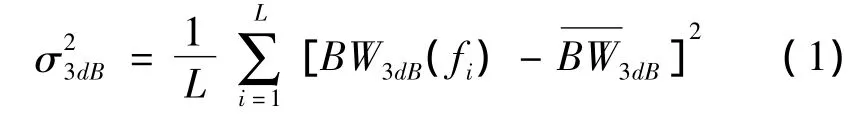
采用基于SOCP的阻带均方误差约束最小通带均方误差滤波器设计方法［2］对阵元滤波器频率响应进行优化，选择参数设置为:阵元数M=12，信号占用归一化频带为［0．175，0．375］，阵元间距 d为归一化频率0.375对应波长λ的1/2，此时在归一化频率0.175上d/λ=1/4，在信号归一化带宽内均匀划分为40个窄带，将 d/λ =1/4、零点束宽BWNN=30o时的Dolphy-Chebyshev加权生成的波束主瓣响应作为期望主瓣响应，取主瓣区角度采样数 ML=64 ，权系数暂取 λ1×ML=11×ML，旁瓣区角度采样数SL=32，旁瓣级约束 μ2=10-1．2=-24dB ，白噪声增益(加权系数范数)μ4=0．5，波束指向法线方向即θo=0o，计算得到样本频点上的3dB束宽方差为，非常接近于零，可见基于SOCP的波束设计和FIR滤波器设计方法可以非常准确的实现样本频点(各子带中心频点)上的恒定束宽。但是FIR滤波器的频率响应是连续的，除了这些样本频点以外，还必须考查它们之间的频点上束宽的变化。在样本频点之间均匀的取5个频点，得到对应的波束图见图1。

此时σ23dB=3．6046，显然束宽的频率稳定性相对于样本频点明显变差，同时，各非样本频点上的波束图不仅出现了主瓣的形变，旁瓣级也明显升高，造成这种现象的原因是整个优化过程只针对样本频点进行，而它们之间的频点未作任何限制，在这些未加控制的频点上出现了图2所示的情况(以第7号阵元FIR滤波器为例)。

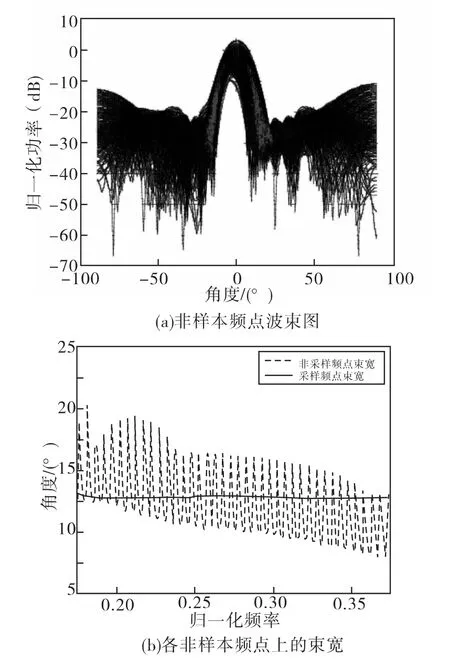
图1 非样本频点上的束宽变化情况

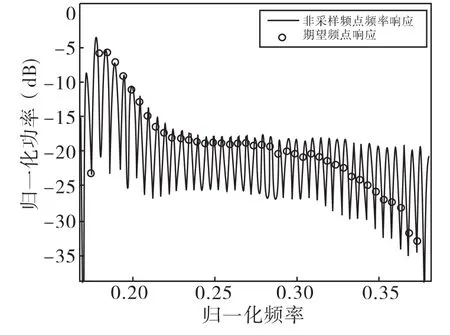
图2 第7号阵元FIR滤波器非样本频点频率响应通带放大图

非样本频点上的频率响应(幅度)本应该与其周围的样本频点相近但却出现了震荡的现象，震荡幅度越大这些非样本频点上的频率响应组成的波束形成器的波束响应与样本频点的波束响应相差越大，导致整个通带上的束宽稳定性下降。

2 非样本频点上频率响应平滑

为了平滑非样本频点上的频率响应，本文进行了大量仿真，最后得到如下结论和解决办法:

a.增大样本频点的密度并不能消除其间非样本频点上频率响应的幅度震荡，在滤波器长度不变时，增大样本频点的密度甚至会导致震荡幅度增大;

b.适当改变通带样本频点数量与阻带样本频点数量的比例可以一定程度的减小非样本频点上频率响应的幅度震荡，但效果并不明显，束宽相对变化率仍然很大;

c.给期望频率响应加上线性相位，可以大幅度减小甚至消除非样本频点频率响应的幅度震荡，明显改善非样本频点的束宽相对变化率提高整个通带上的束宽稳定性。

所谓给期望频率响应加上线性相位，就是设阵元数为M，频率为fi的样本频点上的波束形成加权系数为 Wfi(j)，j=1，2，3，…，M ，第 j个阵元 FIR滤波器的期望频率响应为Hdj(fi)，i=1，2，3，…，L，则有:

此时在上式右边乘以一个线性相位:

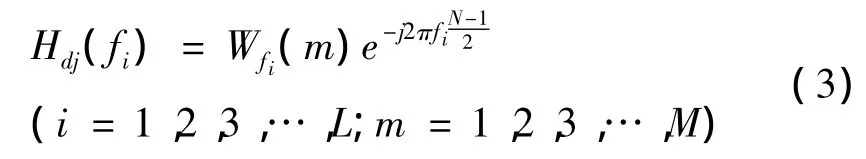
其中N为滤波器长度。加入该线性相位后频点fi上的波束响应为:

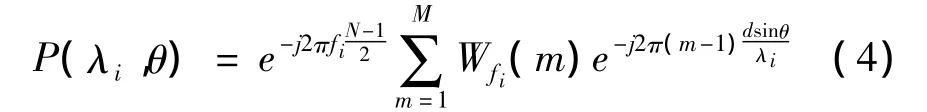
其中λi为fi对应的波长。可以看到线性相位并不会改变该频点上的波束图，且不难证明线性相位最终只是使得输出产生(N-1)/2个采样周期的群延时。取N=201，给期望响应加入线性相位以后图1中非样本频点上的震荡基本消除，最终在非样本频点上的束宽稳定也大大改善，如图3所示。

3 结束语

本文通过仿真分析指出了基于SOCP的宽带波束形成方法存在非样本频点上束宽不稳定的问题;同时分析指出非样本频点上的束宽不稳定是由于阵元FIR滤波器在非样本频点上频率响应未受约束而不规则起伏引起的，为平滑阵元FIR滤波器的频率响应，本文从大量仿真中总结得出给期望频率响应加上线性相位，并适当调整通带采样点数的方法，该方法可以大幅度减小甚至消除非采样频点频率响应的幅度震荡，明显改善非采样频点的束宽相对变化率，提高在整个通带上的束宽稳定性。该方法对于进一步完善基于SOCP的宽带波束形成器设计方法具有积极的参考价值。

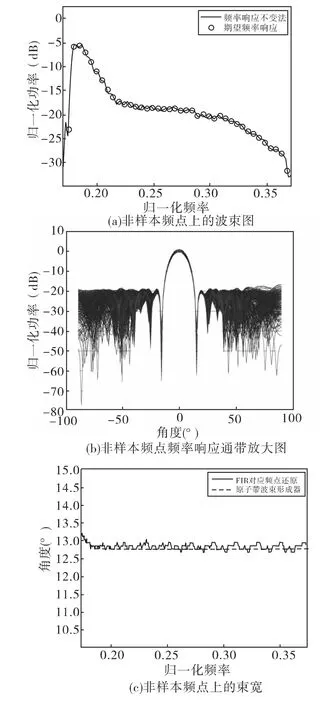
图3 加入线性相位后非样本频点上的束宽变化情况

［1］陈曾平，张月，鲍庆龙.数字阵列雷达及其关键技术进展［J］.国防科技大学学报，2010(6):1-7.

［2］鄢社锋，马远良.传感器阵列波束优化设计与应用［M］.科学出版社，2009:2-194.

［3］杨君.FFT滤波误差分析［J］.通信技术，2010，43(9):235-240.

［4］Yan S.F.，Ma Y.L.，Sun C.Optimal beamforming for arbitrary arrays using second order cone programming［J］.Chinese Journal of A-coustics，2005，24(1):1-9.

［5］王辉.一种基于二阶锥规划的宽带波束形成算法［J］.电子对抗，2013，(4):32-36.

［6］范展，梁国龙.基于凸优化的最小旁瓣恒定束宽时域宽带波束形成［J］.电子学报，2013，41(5):943-948.

［7］Sturm J.F.Using sedumi 1.02，a MATLAB toolbox for optimization over symmetric cones［J］.Optim Methods Software，1999:625-653.