风险分析中的稳健贝叶斯方法
2011-07-09丁东洋刘希阳
丁东洋,刘希阳
(1.南昌大学 公共管理学院,江西 南昌 330031;2.中国人民银行鹰潭市中心支行,江西 鹰潭 335000)
引言
风险分析指处理由不确定性产生的各种问题的一整套方法,包括风险辨识、风险的估计和风险的控制与管理。风险的概念源于经济学,不确定性的概念源于统计决策理论。经济学家奈特定义风险是概率估计的可靠性以及将它作为一种可保险的成本进行处理的可能性,奈特不确定性是指难以通过现有理论或经验对事件可能的结果进行预测和定量分析(Knight,1921)。风险分析概念中的“不确定性”不仅包括奈特不确定性,而且包括风险。风险分析中的计算问题有三个显著特征:某些变量缺少经验数据;采纳分析人员的判断或专家的观点非常必要;构建的数学模型存在不确定性。
贝叶斯方法本身就是用来考察概率模型中与参数相关的不确定性的理论,被公认为正式使用专家观点等主观信息的恰当途径,因而在处理风险分析问题时具有明显的优势。贝叶斯方法对于推断和决策具有统一的理论,而事实上在其方法内部也存在很大差异。例如,绝大多数贝叶斯主义者用主观的方法解释概率并将其作为推断框架中的基本原理,不过也存在一些反对主观概率论的“客观贝叶斯主义者”;多数贝叶斯主义者认为必须简化参数分布以得到单一数值,但也有部分认为可以使用整个分布表现参数的不确定性;贝叶斯主义者多数认为应该而且能够有一种精确的概率模型,而提倡稳健贝叶斯方法的人员则推荐使用一系列的概率模型。
标准贝叶斯方法在风险分析与概率不确定性的研究中地位独特,然而在现实情形违背自身假设的条件下不够稳健。它要求分析人员可以提供的信息多于缺乏数据的风险分析中正常可以获得的信息,给出的标准假设由于低估尾部风险而不够准确。在缺少精确和完全的统计信息时,想要得出可靠的结论需要使用稳健方法。尤其对于风险分析考虑的问题,稳健贝叶斯方法更加适用。本文主要介绍可以应用于风险分析的标准贝叶斯方法与稳健贝叶斯方法。
一、贝叶斯方法在风险分析中的优势与局限性
贝叶斯方法在风险分析中的应用主要有三个途径,第一个途径是用来构建决策框架,全面接管分析和决策过程,对推断和决策提供一套全面的方案;第二个途径是用来估计风险分布,是整个风险分析问题的核心部分,分析得出的数量和分布特征是进行决策的最重要的资料;第三个途径是用来参数化模型,估计模型外生变量的分布而非直接得出结论,作为决策分析过程中的技术支持手段(Scott,2004)。
(一)优势
在风险分析中的应用统计学范围内,普遍关注贝叶斯统计学相对于传统频率统计学的优势。虽然以Fisher,Neyman,Pearson,Gosset等为代表的频率论统计学派在统计学中仍占据主流地位,但贝叶斯学派在过去的四分之一世纪却以惊人的速度成长起来。下面重点介绍其优势的几个方面,目的在于引起风险分析人员对贝叶斯方法的兴趣。
1.有效处理不确定性。贝叶斯理论认为概率是一主观量,而非传统的对有限频率的衡量,从而贝叶斯方法可以计算出一个可信区间①描述参数估计的不确定性。与传统的Neyman-Pearson置信区间②相比,可信区间更加逼真而且易于处理,且在后期的计算中有可行的微积分。贝叶斯理论对模型中的数据和参数都使用概率分布表示,相比而言,频率论方法不允许分布作为模型的常量,因而也往往不能用分布来表述模型参数,仅仅只能考察他们选择的随机数据的概率。贝叶斯方法在数据累积的过程中持续更新,不需要预先设定样本的大小,随时可以停止收集数据,结果的计算和解释不依赖于开始计划的实验设计。这意味着贝叶斯方法有更强的适应性和灵活性,并且对于风险分析问题中可能遇到的极端事件能够给出更准确的推断。
2.便于数据挖掘。贝叶斯方法另一个重要的优点是允许事先对数据有一个大致的了解。传统的Neyman-Pearson学派坚持认为数据挖掘没有科学性,应该逐步实施统计分析,首先准备方案,然后选取数据集,对单一假设计算P值,最后得出结论。而且对只有极少样本的数据建模时,模型中参数的数量不应过多,一次不可以估计太多的参数。实际工作中,分析人员不会也不应该被这些责难所束缚,数据往往都是短缺的,而且在收集的过程中,也不可避免看到数据的大概。只有不断获得新的数据,才有可能认清问题,随之模型也变得越来越复杂。在贝叶斯方法中,事先了解数据十分正常,可以一次估计大量的参数,而且不必过于担心只有少量的数据样本。
3.完整合理决策。贝叶斯方法十分适合进行决策分析,通过将所有的不确定性用概率的形式表现出来,可以保证决策符合一致性,进而使得分析人员和决策者对风险评估和有效管理构建出一致的策略集。传统上,频率论能够给出的唯一结论就是通过数据集判断的是否拒绝原假设,并没有平衡两类错误的成本③,仅仅控制了错误的拒绝原假设的第一类错误。在实际决策时,要给出理由充分的决策,考虑两类成本并且平衡它们非常必要。贝叶斯方法作为决策分析中的基本原理与之结合,可以完整地表述风险管理工作的内涵。虽然目前对风险分析人员还没有要求必须掌握贝叶斯理论,但其从事分析工作的基本知识结构的确是属于贝叶斯方法的范畴。
4.正确使用主观信息。贝叶斯方法在一定程度上使直接使用主观信息得以正式化,创造了一条将主观信息使用于客观方程中的途径,这些信息可能是分析人员的个人判断也可能是专家的观点。在风险分析中,分析人员的经验判断或咨询的专家意见非常有用,忽略这些信息对于缺乏资料的风险分析来说极其浪费。频率论者同样也使用主观信息,如在修改模型结构或改变参数选择时模糊地使用主观信息,然而无法考察这些信息对计算结果的影响。因此贝叶斯主义者直接地说明主观信息好于频率论者模糊地使用这些信息。
(二)局限性
风险分析中使用贝叶斯方法也存在一定不足与局限性,主要在于缺少经验数据使得先验分布的设定比通常更能影响推断结论的准确性,同时必须面对有碍于定量分析的计算困难。这些是在风险分析中使用贝叶斯方法必须面对的难题。
1.先验分布。贝叶斯分析者面对的首要难题就是如何选择先验分布,尤其对于事先并不相信的事件,贝叶斯法则也无法得出任何结论。如改变先验概率,后验分布也将随之改变,即通过转变先验概率的设定可以得到任何可能的概率。虽然随着数据的积累很快会克服和消除先验设定的差异,但是风险分析往往缺少数据。
2.零续存(Zero Preservation)。不论似然函数值多大,也不论出现任何新的数据,先验概率设为零都会导致后验概率为零。同样,不论先验概率的大小,如果似然函数为零,后验概率也将为零。这意味着分析人员如果否认了可能发生的事件,那么任何给出相反信息的事件都无法影响结论。
另外,贝叶斯模型忽略了应该区分不确定性和等概率的差别。如使用平均法描述模型的不确定性,用贝叶斯因子作为模型的权重组成混合模型和分布,缺点是要求分析人员能够列举出所有可能的模型,这在现实中很难克服。即使列举出所有可能的模型,还要分析人员对每个模型的权重指定先验概率,这也是个难题,在风险分析中可能会造成低估风险。
二、稳健贝叶斯方法与风险分析
稳健贝叶斯方法,即贝叶斯敏感性分析,用于研究不确定性问题结论的稳健性(Geweke,2005)。结论如果不敏感地依赖于前提假设和计算使用的外生变量,就表明其具有稳健性。稳健贝叶斯方法认为在很多时候很难提出精确的分布作为先验,用于某一特定问题的似然函数同样值得怀疑。在稳健贝叶斯方法中,所有可能的先验分布与似然函数的结合,都使用标准的贝叶斯方法分析,这也就意味着通过将先验分布与似然函数的两两结合,得到一系列的后验分布。稳健贝叶斯方法还采用类似的策略,将一类概率模型和一类效用函数结合,推断相应的决策,任何可能的答案都针对最佳的概率模型和效用函数给出不确定性。在上述两种情况下,如果在每个组合下给出的结论都近似相同,就表明其具有稳健性;如果结论有明显不同,那么相应范围表示从分析中能获得多大程度的信任。在贝叶斯思想中,不确定性使用单一的附加概率度量,个人的态度及价值使用精确的效用函数表述,这些往往都是出于方便的角度设定,主要是由于成本和时间上的约束不允许花费过多的精力探寻精确的测度函数,稳健贝叶斯方法从表面上来看与这些贝叶斯思想并不一致。Walley(1991)认为稳健方法将无把握性看作有别于不确定性的一类,是传统贝叶斯方法的延伸。
稳健贝叶斯方法涉及来自其他领域一些重要的开创性理念④,这些观点往往可以不用修改而应用到贝叶斯分析中。构建和操作稳健贝叶斯方法有几种途径,包括使用:(1)共轭参数族;(2)非共轭参数族;(3)相对密度(有界密度分布);(4)ε污染、混合及分位数等;(5)累计分布边界。虽然稳健贝叶斯的计算问题比较高深,但有些特殊情况下,其计算也非常直接,下面介绍几种情况:
(一)区间估计
首先定义下面的区间计算公式,其中的x和y代表概率:
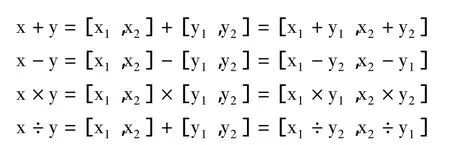
如果x或y是准确的实值s,则其区间可以表示为[s,s],以便在上述公式中使用。Gelman(2003)指出对于每个不确定变量仅使用一次的区间表达运算时,会得到较好的结果。然而区间表达中存在重复的情况,如:
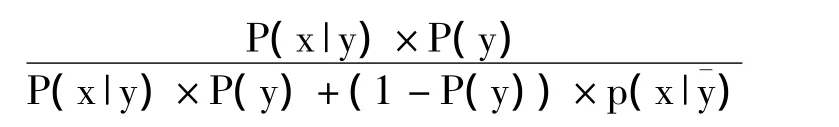
该表达式中p(y)和p(x|y)都出现了多次,普通的区间估计无法对此式进行可靠的分析。如果变量数据有不确定性,那么使用没有重复参数的表达式将是更好的选择:
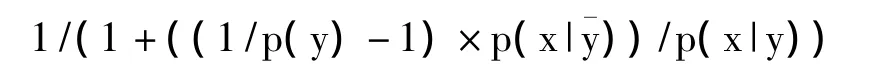
该表达式与原例中的算式是等价的,但是当使用的输入值是区间形式时,会得到更准确的结果。也就是使用没有重复参数的表达式推出的概率将是尽可能小的区间范围。
(二)P-boxes
P-boxes指累积分布函数的上限和下限,通过P-boxes可以对先验分布的不确定性进行定性分析。如果似然函数的不确定性可以通过其积分函数的上下限定性分析,而且限度可以标准化,那么也具有P-boxes形式。在稳健贝叶斯分析中,当先验分布和似然函数的P-boxes被结合起来时,作为后验分布的累积分布函数的限度最有可能是一个矩形P-boxes,即先验分布与似然函数P-boxes的交集。
后验类退化的原因很好理解,在零续存中,如前所述,无论先验还是似然函数为0,后验必定为0。先验分布的P-boxes允许先验累积分布在横坐标一定数值范围内比较平坦,当先验与似然函数都是以边界定性描述的情况下,除了能够知道后验分布的边界外,无法做更多推断。两个P-boxes的形状对推断没有任何关系,唯一有用的是它们的交集。
(三)参数类
稳健贝叶斯分析定义分布类的另一个途径是设其服从参变量。假设有两类分布,一类是方差相同而均值不同,另一类均值相同而方差不同。参数的不同将表示分布的不同,分布族可能是正态的,也可能是由共轭对得出的其他形状,也有可能不是来自于共轭族。参数类表现了分析人员对于先验设定的不确定性,参数的不同也就显示了不确定性。在某种意义上,稳健贝叶斯的参数方法正好存在着与P-boxes中相反的问题,后者是由于类过大而无法对后验做出重要推断,而参数方法是类过小而无法代表先验与似然的不确定性。
(四)有界密度类
使用概率密度代替累积概率也可以绑定先验及似然函数。从二者的界限乘积可以很容易地得出后验函数的密度界限。对于任意θ值,总会有不同的区间绑定先验及似然函数,可以使用区间算法将两个区间相乘。乘积构成了所有可能的非标准化后验分布θ值的上限和下限。如果通过P-boxes方法形成的分布类过于松散且范围过大,参数类形成的分布限定过多且范围过小,则有界密度方法很可能正好适合于实际稳健贝叶斯分析。
需要注意的是,设定一个先验与似然函数,在稳健贝叶斯方法中由于使用了分布类而不受数据缺乏约束,但是稳健贝叶斯仍然受到普通贝叶斯方法的部分问题所限制,如零续存问题。
三、结语
概率论由于开创了把现实世界中的分歧用“概率”表达的途径,在分析应用中非常成功。基于多元化与普遍性的抵触,一些贝叶斯主义者把所有的概率拿来为己所用,并在风险分析中展现出很多相比传统方法的优点。Jaynes(2003)极力主张概率论并非频率的数学科学,而是关于人们对某些事件相对于另外一些事件的信任程度的计算法,但是风险分析人员并非把信任放在首要位置。为了进行风险分析,需要一门关于频率的数学科学,一种允许能够计算分布的计算法,进而直观解释所有可能收集到的数据的权重。同时,需要这种计算法能够利用主观信息,并在一定程度上不能混淆可变性与不确定性。尽管仍具有对于计算困难的恐惧,稳健贝叶斯方法还是修正了贝叶斯方法中很多使人困扰的难题,这也体现了风险分析中概率数学科学的逐步完善。
近年来,统计专业日趋成熟,贝叶斯学派和频率论学派的讨论变得更加包容,双方也都认清了自身的优点与不足。但是在统计学的专业之外,风险分析及其他数学或定量分析的领域,争辩日益激烈,表明了风险分析是一个年轻的蒸蒸日上的领域。分歧的着力点是很难选择某种方法,不同的思想带来了不同的观念,这些可能永远无法理顺,因为这是在没有完全理解世界上人类决策复杂性的表现。但是随着混淆被清除、误解被纠正,不同的观念会互相补充,从而扩大和深化理解风险,风险分析领域将不断完善。
[注 释]
① CredibilityIntervals,根据现有资料能够推出的概率区间.
② Confidence Intervals,根据置信度推出的概率区间.
③ 两类成本分别是当原假设为真时拒绝原假设和当原假设为伪时接受原假设的成本.
④ 如耐抗估计量Resistance Estimator,表示估计量的稳健性.
[1] Knight,F.H.Risk Uncertainty and Profit[M].Boston:Houghton Mifflin,1921.
[2] Scott F.Bayesian Methods in Risk Assessment[R].Working Paper.Head ofWaste & Storage Unit,2004.
[3] Geweke,J.Contemporary Bayesian Econometrics and Statistics[M].New York:Wiley,2005.
[4] Walley,P.Statistical Reasoningwith Imprecise Probabilities[M].London:Chapman-Hall,1991.
[5] Gelman.,A.et.al.Bayesian Data Analysis,2nd ed[M].London:Chapman and Hall,2003.
[6] Jaynes,E.T.Probability Theory[M].Cambridge:Cambridge University Press,2003.
