双门式炮闩膨胀波火炮最佳开闩时机确定和分析

张小嘎，狄长春，郭 博，李杰仁，刘 波

（1.军械工程学院，河北 石家庄 050003；2.驻南阳地区军代室，河南 南阳 474678；3.驻沈阳地区军代局，辽宁 沈阳 110015）

膨胀波火炮的工作原理在火炮发射过程中突然打开炮闩，药室中的火药气体就会向后方喷出，产生反后坐力，药室内的压力即随之下降产生向前传播的膨胀波［1］。根据压力下降传递到弹底的滞后现象，精确控制炮尾打开的时机，使膨胀波恰好在弹丸刚刚脱离炮口的瞬间追赶上弹丸底部，实现“定时同步”［2］。

由此可见精确控制炮闩打开时机和打开方式对膨胀波火炮性能的发挥起着决定性的作用。打开时机过早，膨胀波在弹丸未出炮口前到达弹底影响弹丸的初速；打开时机过晚，减小后坐冲量和降低火炮身管热量的能力不足。本文根据双门式炮闩开闩方式［3］，结合膨胀波火炮的发射机理，建立膨胀波火炮内弹道模型并进行数值仿真，深入研究膨胀波传播速度和行程特性，并分析内弹道模型对最佳开闩时机的影响。

1 双门式炮闩膨胀波火炮结构

目前可以运用到膨胀波火炮系统中的开闩方式主要有惯性炮尾式、主动式爆炸隔板和双门式炮闩。双门式炮闩是最新设计研制的，它摆脱了闩体导杆式的结构模式，使结构布局更加合理，操作更加简单，维护保养更加方便，更有利于今后向工程化应用的转化。其具体的实现过程为：在药室前部、身管中间某位置安置一个导气孔，并通过导管与控制打开炮闩的自锁装置相连。当弹丸运动通过身管中间的导气孔后，火药燃气将被引入导管内冲击自锁装置，达到开启自锁装置的压力后将解除双门式炮闩的约束，使其在瞬间解锁开闩，并导致药室的高压高温火药燃气高速后喷，并向后产生反推力，从而抵消后坐。

内弹道循环过程主要包括开闩前、开闩后到弹丸出炮口以及后效期。其中身管上导气孔的位置为开闩瞬间弹丸在膛内的位置，也是精确控制开闩时机的关键。

2 膨胀波火炮内弹道建模

该模型采用拉格朗日假设，考虑到开闩前后系统本身后坐很小，因此忽略身管后坐对内弹道参量的影响，同时假设开闩过程为瞬时完成。在采用拉格朗日假设时，模型分为不考虑药室和身管之间的截面变化和考虑药室和身管之间的截面变化两种。

2.1 不考虑药室和身管之间截面变化时的内弹道模型

采用经典内弹道零维数学模型，其公式见参考文献［4］，文献中的公式（1）～（5）为计算打开时机和导气孔位置所用的方程。流量公式为：

式中：η为相对流量；Sj为扩张喷管的喷喉面积；ω为发射药质量为流量修正系数；f为火药力；τ为相对温度，τ＝，T为膛内温度，T1为火药定容燃烧温度；θ＝k－1。火药燃气状态方程：

式中：lψ为药室自由容积缩径长；l0s为药室容积缩径长；α为余容；ρp为火药气体密度；Δ为装填密度。

能量平衡方程：

2.2 膨胀波速度和行程求解

膨胀波的特性是只对波前到达区域内介质的流动特性产生影响，对波前未到达区域内介质的流动特性不产生影响，所用可以利用膨胀波的传播特性。假设膨胀波波前在弹丸出炮口瞬间到达弹底，即后喷装置以最佳打开时机打开，此时由于弹丸在整个膛内运动过程始终未受到膛内燃气后喷的影响，弹底区域燃气的流动性质同闭膛条件下保持一致，为此本文利用同类常规闭膛火炮内弹道数据拟合膨胀波在膛内的传播速度，采用反推法，选取弹丸出炮口时刻为初始时刻，以炮口截面中心为初始计算位置，进行倒推计算，进而得到最佳打开时机。

取炮口位置为计算初始值方向计算，并对模型进行简化，如图1所示。

设t时刻弹丸行程为l，膨胀波传播到lr处，此处的气流速度为：

燃气压力为：

燃气密度为：

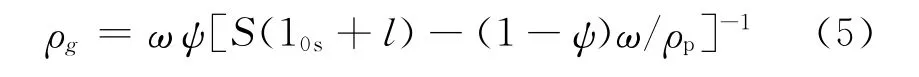
当地声速［5］：

膨胀波速度：

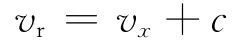
假设弹丸出炮口时间为tpk，取时间步长为Δt，则Δt时刻膨胀波行程为lt，由可得到Δt时刻lg－位置处膨胀波速度；则nΔt时刻膨胀波行程为，直到计算到＝lg，此时对应的时间te＝tpk－nΔt即为最佳开闩时机，弹丸行程l处为导气孔位置，且le＝l。

2.3 考虑药室和身管之间截面变化时的内弹道模型

下面只列出气流速度方程，其他方程和2.1节中所列出的相同，计算方法和2.2中相同。模型简化如图2。

设t时刻弹丸行程为l，膨胀波传播到lr处，此处的气流速度为：

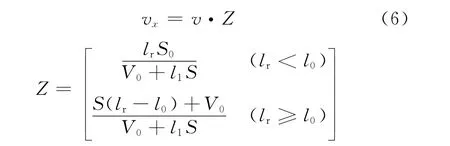
式中：l0为药室长度；V0为药室容积。

3 结果分析

以某口径火炮为计算原型，具体的火炮构造诸元及装填条件见文献［6］，得到了以下结果，如图3～图8所示。

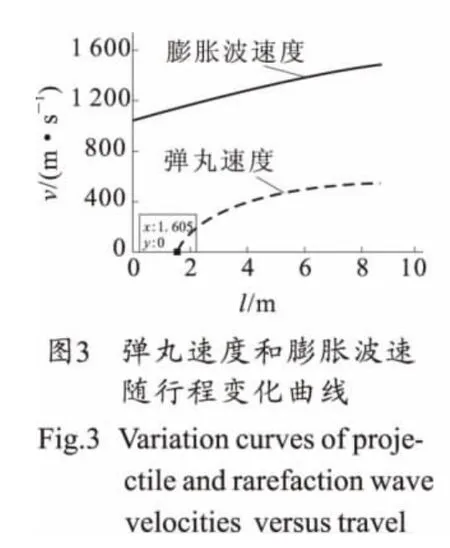
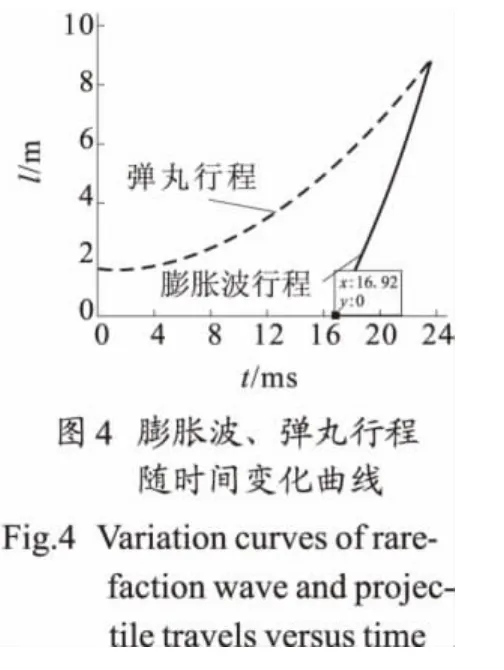
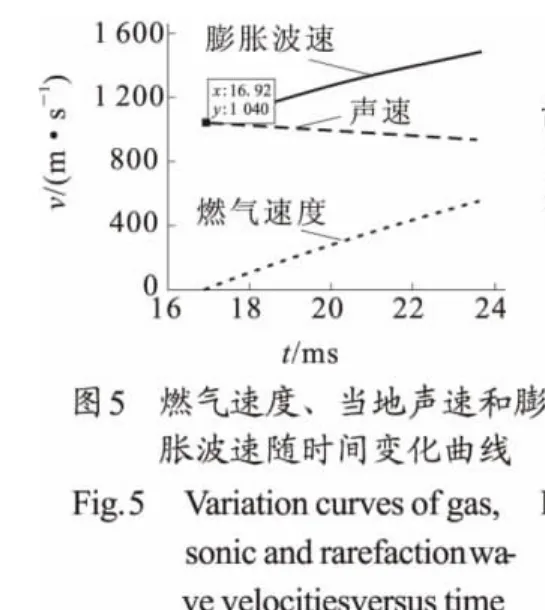
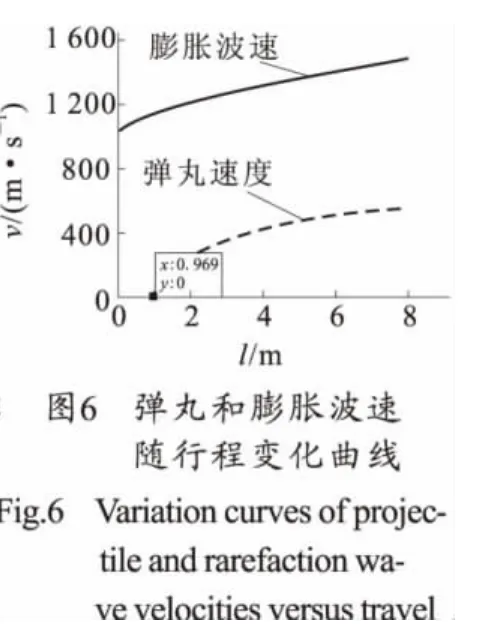
图3～图5是根据模型2所得到的结果，图6～图8是根据模型3所得到的结果。图3和图6都是弹丸速度和膨胀波速度随行程的变化关系，从图3标号知膨胀波起点是1.605m，此长度是药室容积缩颈长，这是简化计算模型2的结果。由图6标号知膨胀波起点是0.969m，是药室长度，是实际的膨胀波起点。图4和图7是膨胀波行程与弹丸行程随时间的变化规律，分别得到喷管打开时机为16.920ms和17.500ms。导气孔位置分别为le＝3.651m和le＝3.920m。图5和图8是燃气速度、当地声速和膨胀波速随时间的叠加关系。由图5和图8标号知喷口打开时膨胀波速分别为1 040 m／s和1 031m／s。

4 结束语

为了解膨胀波火炮内弹道过程的各种动力学现象，笔者针对双门式炮闩膨胀波火炮，建立了膨胀波火炮发射过程模型并求解，根据不同模型得到了不同的打开时机和导气孔位置，这两点是膨胀波火炮开闩的关键，对于膨胀波火炮系统的实际应用具有指导意义。由于条件有限，本文只给出了仿真结果。

（References）

［1］KATHE E.Sonic rarefaction wave recoilless gun system［P］.USA：09／631，142，2000.

［2］张帆，廖振强，王涛，等.膨胀波枪炮发射原理数值建模与分析［J］.南京理工大学学报，2007（1）：17－21.ZHANG Fan，LIAO Zhen－qiang，WANG Tao，et al.Numerical modeling and analysis on rarefaction wave gun［J］.Journal of Nanjing University of Science and Technology，2007（1）：17－21.（in Chinese）

［3］ZHI Jian－zhuang，ZHENG Jian.Modeling and simulation about rarefaction wave gun interior ballistics appling two－door breechblock［C］.ISTM／2009.Taiyuan，2009.1107－1110.

［4］金志明，袁亚雄，宋明.现代内弹道学［M］.北京：北京理工大学出版社，1992：25－26.JIN Zhi－ming，YUAN Ya－xiong，SONG Ming.Modern interior ballistics［M］.Beijing：Beijing Institute of Technology Press，1992：25－26.（in Chinese）

［5］KATHE E.Rarefaction wave gun propulsion［D］.Troy，NY：Rensselaer Polytechnic Institute，2002.

［6］王连荣，张佩勤.火炮内弹道计算手册［M］.北京：国防工业出版社 ，1987：34－35.WANG Lian－rong，ZHANG Pei－qin.Reckoner of gun interior ballistics［M］.Beijing：National Defence Industrial Press.1987：34－35.（in Chinese）